MATS1

This entry is used if a MAT1 entry is specified with the same MID in a nonlinear subcase.

Format A (HR = 1 to 3)

Example A (HR = 1, 2, 3)

Format B.1 (HR = 6: Kinematic Hardening (NLKIN), TYPKIN=PARAM)

Format B.2 (HR = 6: Kinematic Hardening (NLKIN), TYPKIN=HALFCYCL)

Format B.3 (HR = 6: Isotropic Hardening (NLISO), TYPISO=PARAM)

Format B.4 (HR = 6: Isotropic Hardening (NLISO), TYPISO=TABLE)

Example (HR = 6): Kinematic Hardening

Example (HR = 6): Combined Hardening

TYPKIN=PARAM, NLKIN=2, Temperature-dependent

Example (HR = 6): Kinematic Hardening

Definitions

Comments

1. String based labels allow for easier visual identification, including when being referenced by other entries (example, the MID field of properties). For more details, refer to String Label Based Input File.
2. For elastoplastic materials, the elastic stress-strain matrix is computed from the MAT1 entry, and the isotropic plasticity theory is used to perform the plastic analysis.

   Either the table identification TID or the work hardening slope H may be specified, but not both.

3. If TID is given, TABLES1, TABLEG , TABLEST or TABLEMD entries (Xi,Yi) of stress-strain data ( $\text{ε}$ _x,Y_x) must conform to the following:

   Entity	TYPE = PLASTIC
   Quadrant	Plastic stress-strain curve must be defined in the first quadrant only.
   First point	If TYPSTRN = 0, First point must be at the origin (X1=0, Y1=0). Second point (X2, Y2) must be the initial yield stress (Y2=LIMIT1) at initial yield strain (X2=LIMIT1/E). The slope of the line joining the origin to the initial yield stress must be equal to the value of E. If TYPSTRN=1, First point (X1, Y1) is corresponding to initial yield stress (Y1=LIMIT1), with zero equivalent plastic strain (X1=0).
   Additional details	The data points must be in ascending order. If TYPSTRN=1, TID may reference a TABLEST entry. In this case, the above rules apply to all TABLES1 tables pointed to by TABLEST.

   • In case of small deformations, the true and the engineering stress-strain curves are almost the same,so either of them can be used in the table definition.
   • In case of large deformations, the true stress-strain curve should be used.
   • If the deformations exceed the values defined in the table, linear extrapolation is performed.
4. When TID refers to TABLEMD, the following applies:

   Xi_j	Implicit Analysis (NLSTAT/Nonlinear Transient Analysis for SMDISP/LGDISP)	Explicit Analysis
   Xi_1	Equivalent plastic strain. This can be used for both rate-dependent and independent problems.	Represents plastic or total strain in case of rate-independent problems.
   Xi_2	Represents plastic strain rate in case of rate-dependent problems. If only one value of X2 is specified, it is still rate independent.	Represents plastic or total strain rate in case of rate-dependent problems.
   Xi_3	Temperature	N/A

5. Information about rate dependent plasticity:

   Entity	Implicit Analysis (NLSTAT/Nonlinear Transient Analysis for SMDISP/LGDISP)	Explicit Analysis
   Activation	Rate dependent plasticity can be activated by specifying TABLEMD ID in the TID field. This uses a piecewise linear function.	Rate dependent plasticity can be activated in several ways. Specifying TABLEMD ID in TID field. This uses a piecewise linear function. Johnson-Cook model (only when the strain rate is greater than RSTRT). Crushable Foam model. Cowper-Symonds model.
   Elements	Solid elements only.	Shell and solid elements.
   Temperature dependent rate dependent plasticity	Supported. The temperature-dependence is defined by referencing a TABLEST entry via the TID field.	Not supported.
   TABLEMD definition	A maximum of 4 fields can be used in TABLEMD, which represent, Yield stress Equivalent plastic strain Plastic strain rate Temperature Currently, only experimental data can be used. A stress-strain curve at zero plastic strain rate must be provided.	A maximum of three fields can be used in TABLEMD, which represent, Yield stress Equivalent plastic strain Plastic/total/volumetric strain rate
   Supported strain rates	Only plastic strain rate is supported. Hence, total strain rate input (TYPSTRT=0) is ignored.	Plastic/total/volumetric strain rate is supported.
   Additional remarks	Total strain input (TYPSTRN=0) is not supported and ignored. The second column in TABLEMD must be the equivalent plastic strain.

   Mixed hardening (HR=1, 2, 3 or real value) can be combined with rate dependent plasticity (TID=TABLEMD).

6. Support information for kinematic and mixed hardening:

   Supported Entity	Implicit Analysis (NLSTAT and Nonlinear Transient Analysis)	Explicit Analysis
   Elements	SMDISP Shell (1st order) and solid elements LGDISP Shell (1st order) and Solid elements	Shell and solid elements

7. The conversion of the stress versus total strain (TYPSTRN=0) into stress versus plastic strain (TYPSTRN=1) is illustrated in Figure 1. This is clearly different than simply shifting the entire table along the epsilon-axis.

   
   
   

8. Element support restrictions for MATS1:

   Element Type

   Restriction

   Second order shell elements (CTRIA6 and CQUAD8)

   • MATS1 is not supported

   CROD, CONROD, CBAR and CBEAM

   • MATS1 is supported in the axial translational direction only
   • The behaviors in other directions remain elastic. More specifically, the torsional deformation of the CROD/CONROD elements or the shear, bending and torsional deformations of the CBAR/CBEAM elements remain elastic.

9. Information on the Johnson-Cook model:

   Entity

   Details

   Analysis type

   Supported only for Explicit Dynamic Analysis

   Strain rate dependency

   Activated only when strain rate is greater than reference strain rate

   Formulation:
   $$\sigma =\left(a+b{\epsilon }_p^n\right)\left(1+c\ln \left(\frac{\dot{\epsilon }}{{\dot{\epsilon }}_0}\right)\right)$$
   $$\overline{\sigma }=\left(A+B{\left({\overline{\epsilon }}^{pl}\right)}^n\right)\left(1+C\ln \left(\frac{{\dot{\overline{\epsilon }}}^{pl}}{{\dot{\epsilon }}_0}\right)\right)$$

   Johnson-Cook strain rate dependence assumes that

   $$\overline{\sigma }={\sigma }^0\left({\overline{\epsilon }}^{pl},\theta \right)R\left({\dot{\overline{\epsilon }}}^{pl}\right)$$

   and ${\dot{\overline{\epsilon }}}^{pl}={\dot{\epsilon }}_0\exp \left(\frac{1}{C}\left(R-1\right)\right)$ for $\overline{\sigma }\ge {\sigma }^0$ .

   Where,

   $\overline{\sigma }$

   Yield stress for non-zero strain rate

   ${\overline{\epsilon }}^{pl}$

   Equivalent plastic strain rate

   ${\dot{\epsilon }}_0$ and $C$

   Material parameters measured at or below the transition temperature ${\theta }_{transition}$

   ${\sigma }^0\left({\overline{\epsilon }}^{pl},\theta \right)$

   Static yield stress

   $R\left({\dot{\overline{\epsilon }}}^{pl}\right)$

   Ratio of the yield stress at nonzero strain rate to the static yield stress $R\left({\dot{\epsilon }}_0\right)=1.0$

10. Information on the Crushable Foam model:

    Entity

    Details

    Analysis type

    Supported only for Explicit Dynamic Analysis

    TSC definition

    Defined as a positive stress value which indicates the yield stress of crushable foam under tensile loading

    Table definition

    The yield stress of crushable foam under compression loading can be given by a rate independent table (TABLES1) where the following rules apply:

    • x values in the table are the volumetric strain (all positive values indicate that the volume is compressed). The volumetric strain is defined as $\gamma =1-\frac{V}{V_0}$ .
    • y values in the table are the compression yield stress (all positive values).
      Note: Since crushable foam is based on volumetric strain-based definition, TYPSTRN=0 (default) is invalid and TYPSTRN=1 must be specified.
    • First entry is x=0, y=y_0 (the initial compressive yield stress).
    • All xi should be positive and in increasing order.

    Specific output

    Instead of the equivalent plastic strain, the integrated volumetric strain result (natural logarithm of the relative volume $-In\left(\frac{V}{V_0}\right)$ is output.

11. Information on the Cowper-Symonds model:

    Entity

    Details

    Analysis type

    Supported only for Explicit Dynamic Analysis

    TYPSTRT

    Either total strain rate or plastic strain rate can be used

    $f\left({\epsilon }^{pl}\right)$

    Can be specified in linear hardening form or tabular form using TABLES1 or TABLEMD

    Formulation:

    The yield stress is computed as:

    $${\sigma }_y=\beta f\left({\epsilon }^{pl}\right)$$
    Where,

    $f\left({\epsilon }^{pl}\right)$

    Reference rate plastic strain versus yield stress hardening function.

    $\beta$

    Strain rate effect term, computed as $\beta =1+{\left(\frac{\dot{\epsilon }}{D}\right)}^{\frac{1}{p}}$ .

12. Information on using combined hardening:

    Entity

    Details

    Analysis type

    Supported only for Implicit Analysis (Nonlinear Static and Transient for SMDISP/LGDISP)

    Element type

    Supported only for solid elements

    Rate dependent plasticity with combined hardening

    Not supported, thus TID field is ignored

    Flexibility in combination

    Both NLKIN and NLISO support either parameter or stress-strain curve input.

    They can be combined flexibly, for example NLKIN with parameter input (PARAM) and NLISO with stress-strain curve input (TABLE).

    At least one type of nonlinear hardening should be defined. For more information, refer to the Combined Hardening of von Mises Plasticity.

13. Information on using NLKIN or NLISO:

    Entity

    Details

    Analysis type

    Supported only for Implicit Analysis (NLSTAT/Nonlinear Transient Analysis for SMDISP/LGDISP)

    Temperature dependency

    When TYPKIN = HALFCYCL or TYPISO = TABLE, multiple curves can be provided one after each other. The last column temperature (TEMP) should be in ascending order. When TYPKIN/TYPISO = PARAM, the parameters can be temperature dependent, with TEMP specified in ascending order.

    Parameter fitting (for TABLE/HALFCYCL)

    The Levenberg-Marquardt method is used.

    The parameters are printed in the .out file for each temperature.

    Equivalent plastic strain determination

    For NLKIN, it is usually sourced directly from the first cycle of the experiment. For NLISO, it is usually sourced from cyclic loading experiments.

    Additional remarks

    If both NLKIN and NLISO use PARAM format, then the initial yield stress SIGY0 should be the same for the same temperature.

    After the continuation line, an unlimited number of continuation lines can be added to the data block.

14. When TYPKIN=PARAM, if the number of back stresses is equal to or greater than 4, multiple continuation lines can be used to define the complete set of parameters (C1-C10, G1-G10). See the example above.
15. Temperature-dependent materials can be activated at the subcase level via different options (such as TEMP(MAT), TEMP(BOTH), DLOAD (via TLOAD1, TLOAD2 and TEMP/TEMPD Bulk Data Entries), etc.) depending on the subcase type.
16. Temperature-dependent material can be activated at the subcase-level via different options (such as TEMP(MAT), TEMP(BOTH), DLOAD (via TLOAD# and TEMP/TEMPD Bulk Data Entries), and so on ...) depending on the subcase type. For more information, refer to Comment 2 on the TEMPERATURE Subcase Information Entry.
17. The damage initiation and evolution failure criteria can be defined using two methods:
    • Using the DAMAGE continuation line in the MATS1 Bulk Data Entry. This method is supported both for Implicit and Explicit Dynamic Analysis.
    • Using CRI=INIEVO in the MATF Bulk Data Entry. This method is supported only for Explicit Dynamic Analysis.

    For more information, refer to Material Failure Criterion in the Explicit Dynamic Analysis section of the User Guide.

18. The Johnson-Holmquist material model is available to model brittle material behavior. It can be used with MAT1 elastic behavior and is currently only supported for solid elements. The shear modulus ( $G$ ) and bulk modulus ( $K_1$ ) can be used to input the corresponding Young's modulus and Poisson's ratio as:
    $$E=\frac{9K_{1}G}{3K_1+G}$$ $$\nu =\frac{3K_1-2G}{6K_1+2G}$$

    The equivalent stress is the normalized Von Mises stress:

    $${\sigma }_{VM}^{*}=\frac{1}{{\sigma }_{HEL}}\sqrt{\frac{3}{2}\left({\sigma }_{xx}^2+{\sigma }_{yy}^2+{\sigma }_{zz}^2+2{\sigma }_{xy}^2+2{\sigma }_{yz}^2+2{\sigma }_{zx}^2\right)}$$
    Where the normalizing stress is the Hugoniot elastic limit is calculated as:
    $${\sigma }_{HEL}=\frac{3}{2}\left(HEL-P_{HEL}\right)$$

    The normalized Von Mises stress, ${\sigma }_{VM}^{*}$ is compared to the normalized yield stress ${\sigma }^{*}$ obtained with:

    $${\sigma }^{*}=\left(1-D\right){\sigma }_i^{*}+D{\sigma }_f^{*}$$

    Where,

    ${\sigma }_i^{*}$

    Intact material yield stress: ${\sigma }_i^{*}=a{\left(P^{*}+T^{*}\right)}^n\left(1+c\ln \left(\frac{\dot{\epsilon }}{{\dot{\epsilon }}_0}\right)\right)$

    ${\alpha }_f^{*}$

    Failed material yield stress: ${\sigma }_f^{*}=b{\left(P^{*}\right)}^m\left(1+c\ln \left(\frac{\dot{\epsilon }}{{\dot{\epsilon }}_0}\right)\right)<{\sigma }_{fmax}^{*}$

    Where,

    $$\sigma *=\frac{\sigma }{{\sigma }_{HEL}}$$

    $$P^{*}=\frac{P}{P_{HEL}}$$

    $$T^{*}=\frac{T}{P_{HEL}}$$

    If no damage parameters are specified $(D_1=D_2=0)$ , no plastic strain evolution is computed and an instant failure is obtained when the element behavior reaches the elastic limit. Otherwise, when damage parameters are mentioned, the plastic strain evolution is computed and the accumulated damage is:

    $$D=\frac{\sum \mathrm{\Delta }{\epsilon }_f^p}{{\epsilon }_f^p}$$

    Where the plastic strain to failure is calculated as:

    $${\epsilon }_f^p=D_1{\left(P^{*}+T^{*}\right)}^{D_2}$$

    The maximum pressure tensile strength is decreased during damage as:

    $$P^{*}=-\left(1-D\right)T^{*}$$

    This allows a smoother transition between ${\sigma }_i^{*}$ and ${\sigma }_f^{*}$ during damage.

    
    
    

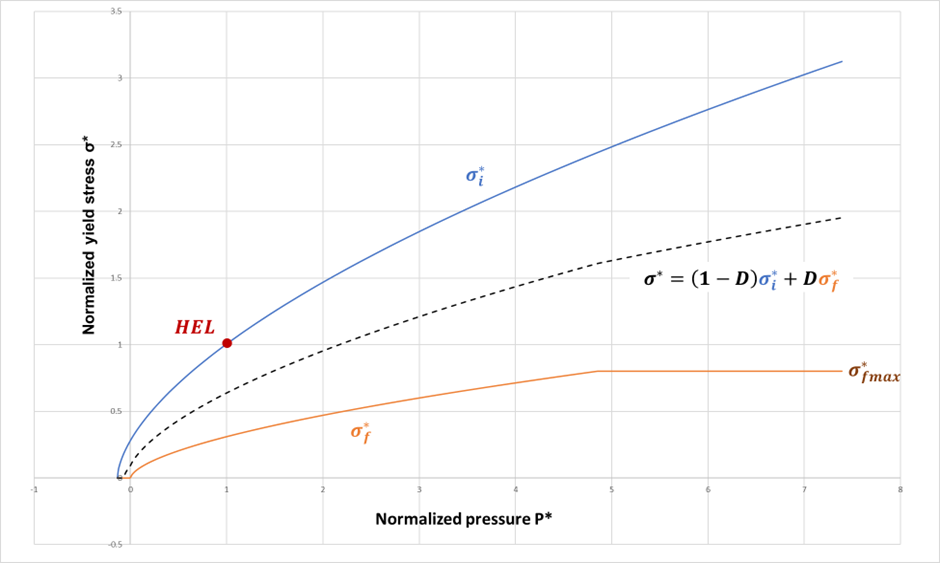
    The pressure is computed following an equation of state defined as:

    $$P=K_1\mu$$
    in tension, and
    $$P=K_1\mu +K_2{\mu }^2+K_3{\mu }^3$$
    in compression

    Where:

    $$\mu =\frac{\rho }{{\rho }_0}-1$$

    When damage starts, a bulking pressure increment $\Delta P$ is computed as a function of elastic energy loss $\Delta U$ converted into potential hydrostatic energy:

    $$\Delta P_{t+\Delta t}=-K_1\mu +\sqrt{{\left(K_1\mu +\Delta P_t\right)}^2+2\beta K_1\Delta U}$$

    Where $\Delta U=U\left(D\right)-U\left(D_{n+1}\right)$ , with $U\left(D\right)=\frac{\sigma }{6G}$ .

    This increment is then added to the equation of state described above:

    $$P_{t+\Delta t}=P_t+\Delta P_{t+\Delta t}$$

19. When some nonlinear material models which are currently only supported for explicit analysis, such as Johnson-Cook, Crushable Foam, Cowper-Symonds, and Johnson-Holmquist materials, are used for implicit analysis subcases, only the linear elastic part of these materials is considered for implicit analysis. A corresponding WARNING message is also printed to the .out file.