Materials
The different material types provided by OptiStruct are: isotropic, orthotropic, and anisotropic materials. The material property definition cards are used to define the properties for each of the materials used in a structural model.
The MAT1 Bulk Data Entry is used to define the properties for isotropic elastic materials. It can be referenced by any of the structural elements and can also be referenced by any property card.
The MAT2 entry is used to define the properties for anisotropic materials. It applies only to triangular or quadrilateral membrane and bending elements, and can only be referenced by PSHELL, PCOMP, and PCOMPG property cards. This material type specifies the relationship between the in-plane stresses and strains. The angle between the material coordinate system and the element coordinate system is specified on the connection cards.
The MAT3 entry is used to define the material properties for axisymmetric and plane-strain elements. It can be referenced by CTRIAX6 elements and can also be referenced by any PAXI property card which is in turn referenced on CTAXI or CQAXI elements. Similarly, it can be referenced by the PPLANE property which is referenced by plane-strain CQPSTN and CTPSTN elements.
The MAT4 entry is used to define the isotropic thermal material properties. It can be referenced by any of the structural elements, and can also be referenced by any property card.
The MAT5 entry is used to define the anisotropic thermal material properties. It can be referenced by any of the structural elements and can also be referenced by any property card.
The MAT8 card is used to define the properties for planar orthotropic elastic materials in two dimensions. Individual plys of a layered composite lay-up typically possess such orthotropic properties. Since layered composite laminates are modeled using shell elements, MAT8 property data can only be referenced by PSHELL, PCOMP, and PCOMPG property cards.
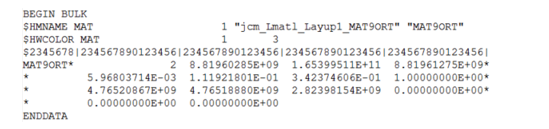
The MAT9 Bulk Data Entry can be used to define the properties for anisotropic elastic materials for three dimensional solid elements. The general an-isotropic stress-strain relationship linking the six independent stress components of the stress tensor at a point and the six independent strain components of the tensor at the point contain 21 independent constants in the elasticity matrix. These values are supplied using the MAT9 Bulk Data card. The MAT9 Bulk Data card is used with the CHEXA, CPENTA, CPYRA, and CTETRA solid elements, and can only be referenced on the PSOLID property card. The optional coordinate system in which MAT9 data are specified is supplied via the PSOLID Bulk Data Entry.
The MAT10 Bulk Data Entry is used to define material properties for fluid elements in coupled fluid-structural (acoustic) analysis. It may only be referenced on PSOLID entries with FCTN=PFLUID.
Biot (poroelastic) material is defined using MATPE1 entry.
Temperature dependent material properties are defined using MATT1, MATT2, MATT8, and MATT9. All four have the same characteristics as described above. The temperature dependency of each property is defined through TABLEM1, TABLEM2, TABLEM3, or TABLEM4 table entries.
Composite Laminates are defined using the PCOMP, PCOMPP and PCOMPG properties. They are not material types; each ply in the laminate lay-up can reference a different material.
Elasto-plastic material properties are defined using MATS1. The nonlinear material characteristics may need the table input TABLES1. MATS1 is defined as an extension to a MAT1 with the same MID. MATS1 is applicable to all nonlinear solutions.
Hyperelastic material properties are defined using MATHE. Various Hyperelastic material models are available, such are Ogden, Arruda-Boyce, and so on.
Viscoelastic material properties are defined using MATVE, MATTVE (temperature-dependent) or MATFVE (frequency-dependent).
Creep material properties are defined using MATVP.
Cohesive Zone Modeling can be defined using MCOHE or MCOHED entries.
Cast Iron Plasticity material can be defined using MCIRON Bulk Data Entry.
User-defined structural material properties are available using MATUSR. .dll or .so libraries can be referenced via the LOADLIB entry. For more information, refer to User-Defined Structural Material in the User Guide.
User-defined thermal material properties are available using MATUSHT. .dll or .so libraries can be referenced via the LOADLIB entry.
Material models can also be defined using Multiscale Designer and used via the MATMDS entry.
A Brittle Damage material model is available via the MATBRT entry.
| Material Property | Nonlinearity | Time-dependency | Temperature-dependency | Frequency-dependency | Material Entry |
|---|---|---|---|---|---|
| Isotropic | - | - | - | - | MAT1 |
| - | - | - | Yes | MAT1 + MATF1 | |
| - | - | Yes | - | MAT1 + MATT1 | |
| Elasto-plasticity | - | - | - | MAT1 + MATS1 | |
| - | Yes | - | MAT1 + MATS1 (referencing TABLEST) | ||
| Hyperelasticity | - | - | - | MATHE | |
| - | Yes | - | MATTHE | ||
| Viscoelasticity | - | - | - | MAT1 + MATVE | |
| - | Yes | - | MAT1 + MATVE + MATTVE | ||
| - | - | Yes | MAT1 + MATVE + MATFVE | ||
| Viscoelasticity, Hyperelasticity | - | - | - | MATHE + MATVE | |
| Creep | - | - | - | MAT1 + MATVP | |
| Creep, Elasto-plasticity | - | - | - | MAT1 + MATVP + MATS1 | |
| Creep | - | Yes | - | MAT1 + MATVP + MATTVP | |
| Anisotropic | - | - | - | - | MAT9 (solid
elements) MAT2 (shell elements) |
| - | - | - | Yes | MAT9 + MATF9 (solid
elements) MAT2 + MATF2 (shell elements) |
|
| - | - | Yes | - | MAT9 + MATT9 (solid
elements) MAT2 + MATT2 (shell elements) |
|
| Viscoelasticity | - | - | - | MAT9 + MATVE | |
| - | - | Yes | MAT9 + MATFVE | ||
| Orthotropic | - | - | - | - | MAT9OR (solid
elements) MAT8 (shell elements) MAT3 (axisymmetric and plane strain elements) |
| - | - | - | Yes | MAT8 + MATF8 (shell
elements) MAT3 + MATF3 (axisymmetric and plane strain elements) |
|
| - | - | Yes | - | MAT9OR + MATT9OR (solid
elements) MAT8 + MATT8 (shell elements) MAT3 + MATT3 (axisymmetric and plane strain elements) |
|
| Fluid | - | - | - | - | MAT10 |
| - | - | - | Yes | MAT10 + MATF10 | |
| Thermal | - | - | - | - | MAT4 (Isotropic) MAT5 (Anisotropic) |
| Yes (Temperature) | - | Yes | - | MAT4 + MATT4 (Isotropic) | |
| Gasket | - | - | Yes | - | MGASK |
| Fatigue | - | - | - | - | MATFAT |
| Biot (Poroelasticity) | - | - | - | - | MATPE1 |
| User-Defined Structural Material Subroutines | Yes | Yes | Yes | - | MATUSR (Fortran and C for subroutines) |
| User-Defined Thermal Material Subroutines | Yes (Temperature) | Yes | Yes | - | MATUSHT (Fortran and C for subroutines) |
| Multiscale Designer-based Material | Yes | - | - | - | MATMDS (using Altair Multiscale Designer). |
| Failure Criteria | - | - | - | - | Criteria and Allowables on
MATF Criteria/Allowables can also be defined on MAT1, MAT2, MAT8, PCOMP, PCOMPP, PCOMPG |
| Material Property | Nonlinearity | Time-dependency | Temperature-dependency | Frequency-dependency | Material Card |
|---|---|---|---|---|---|
| Isotropic | - | - | - | - | MAT1 |
| Elasto-plasticity | - | - | - | MAT1 + MATS1 | |
| Hyperelasticity | - | - | - | MATHE | |
| Viscoelasticity | - | - | - | MAT1 + MATVE | |
| Viscoelasticity, Hyperelasticity | - | - | - | MATHE + MATVE | |
| Anisotropic | - | - | - | - | MAT2 (shell elements) |
| Viscoelasticity | - | - | - | MAT9 + MATVE | |
| Orthotropic | - | - | - | - | MAT8 (shell elements) |
| Brittle Damage | MATBRT |
User-Defined Structural Material
The MATUSR Bulk Data Entry, in combination with the LOADLIB I/O Option Entry, allows for the definition of structural material through user-defined external functions.
The external functions may be written in Fortran, C or C++. The resulting libraries and files should be accessible by OptiStruct regardless of the coding language, provided that consistent function prototyping is respected, and adequate compiling and linking options are used.
Write External Functions
Two Fortran subroutines are required to define user material in OptiStruct. First, a Nonlinear subroutine for the nonlinear large displacement solution, and another subroutine for the linear and nonlinear small displacement solution. Both subroutines are mandatory, and the same argument order should be followed as:
subroutine usermaterial(idu,stress,
$ strain,dstrain,dfgrOld,dfgrNew,
$ stater,state,nstate,
$ drot,
$ props,nprops,ndi,nshear,ntens,temp,dtemp,
$ ieuid,
$ kinc,dt,t_step,t_total,
$ cdev,cbulk)
integer idu, nstate, nprops, kinc, ieuid, ndi, nshear, ntens, ierr
double precision stress(6),stater(*),state(*),
$ cdev(6,6),cbulk, drot(3,3), temp, dtemp, dt,
$ t_step, t_total,
$ strain(6), dstrain(6), props(nprops)
$ dfgrOld(3,3),dfgrNew(3,3)
character*32000 userdatasubroutine smatusr(idu, nprop, prop, ndi, nshear, ntens, smat, userdata, ierr)
integer idu, nprop, ndi, nshear, ntens, ierr
double precision prop(nprop), smat(*)
character*32000 userdatainitusr subroutine:subroutine initusr(idu,nstate,cstate)
implicit none
integer idu,nstate
character*64 cstate(nstate)initusr
subroutine should always be declared as
follows: character*64 cstate(nstate)cstate variable can be assigned the label to
print in the user-defined results with 1 being the index for the
first variable in the example
below: cstate(1) = “Variable Name for State(1)”Subroutine Arguments
| Argument | Type | Input / Output | Description |
|---|---|---|---|
idu |
integer | Input | This is defined via the USUBID parameter
on the MATUSR Bulk Data Entry. This argument
can be used to define and choose between different types of
materials within the same user subroutine. optional use |
stress |
double (table) | Input/Output | This is the Stress tensor. The initial stress is considered to be input and the stress, tensor calculated during the nonlinear solution are output from the user subroutine to OptiStruct. |
strain |
double (table) | Input | Strain tensor. The initial strain is considered to be input. |
dstrain |
double (table) | Input | Incremental strain table. The incremental strain is input from OptiStruct to the user subroutine. |
dfgrOld |
double (table) | Input | Deformation gradient tensor of the previous increment. This argument is currently supported for solid elements (PSOLID) or continuum shells (PCOMPLS). |
dfgrNew |
double (table) | Input | Deformation gradient tensor of the current increment. This argument is currently supported for solid elements (PSOLID) or continuum shells (PCOMPLS). |
stater |
double (table) | Input/Output | Table of State variables at the previous increment. |
state |
double (table) | Input/Output | Table of State variables at the current increment. See
stater for more information. State
variables are variables that can be requested as output in the
H3D file. Any variable (for example, plastic strain, equivalent
plastic strain, and so on) calculated within the solution
process in the subroutine can be output by defining it as a
state variable. The number of state variables can be specified
via nstate. |
nstate |
integer | Input/Output | Number of State Variables that the user requires in the
subroutine. These state variables are output in the H3D file.
See stater for more information. This is
specified via the NDEPVAR field of the
MATUSR Bulk Data Entry. |
cstate |
string | Output | Output in the form of a string from initusr
subroutine to OptiStruct. In the
usermaterial or smatusr
subroutines the state variable outputs any variable in the
H3D file. The cstate
variable provides the name of the state variable declared in
that subroutine to display in the H3D
file. |
props |
double (table) | Input | This table contains all the user-defined material property information from the PROPERTY continuation line of the MATUSR entry. |
nprops |
Integer | Input | This is the total number of material properties defined on the PROPERTY continuation line of the MATUSR entry. |
ndi |
Integer | Input | The number of normal stress components (3 for solid elements, 2 for shell elements). |
nshear |
Integer | Input | The number of shear stress components (3 for solid elements, 1 for shell elements). |
ntens |
Integer | Input | The number of tensor components (ntens =
ndi + nshear). |
temp |
double | Input | This is the temperature at the previous converged increment. |
dtemp |
double | Input | This is the temperature increment. |
ieuid |
integer | Input | Element ID. This subroutine is called for every integration point for every element. |
kinc |
integer | Input | Current increment. |
dt |
double | Input | Current Time increment |
t_step |
double | Input | Subcase time. |
t_total |
double | Input | Total time (if CNTNLSUB is used) |
cdev |
double (table) | Output | Full material modulus matrix of size (6x6). These are calculated during the solution and are output to OptiStruct to form the stiffness matrix. |
cbulk |
double (table) | Output | (Optional) Bulk material modulus Matrix. |
smat |
Double (table) | Output | 1D array (21 terms). This is the symmetric part of
cdev. These are calculated during the
solution and are output to OptiStruct to form the stiffness matrix. |
userdata |
Character | Output | User-defined message that is output based on the value of
ierr argument. |
ierr |
Integer | Input/Output | Flag that activates/deactivates Output message for an
OptiStruct run from the user
subroutine.
|
Build External Libraries for User-defined Materials
Allows building shared libraries on Windows or Linux.
Refer to Build External Libraries for more information.
User-Defined Thermal Material
The MATUSHT Bulk Data Entry, in combination with the LOADLIB I/O Option Entry, allows for the definition of thermal material through user-defined external functions.
Write External Functions
subroutine usrmatht(idu, matID, ieuid,
Integration_Point, Layer, Simpson_Point,
Stater, State,
nState, drot, props, nprops, temp,
dtemp, kinc, dt, t_step, t_total, hgen, smat
userdata, ierr)
character*32000 userdata
integer*8 i, idu, matID, ieuid, nState, nprops, kinc, ierr
integer Integration_Point, Layer, Simpson_Point
double precision Stater(nState), State(nState)
double precision drot(3,3), rmat(nprops)
double precision etempmat, dtemp, dt, t_step, t_total
double precision hgen, smat(9)initusr subroutine:subroutine initusr(idu,nstate,cstate)
implicit none
integer idu,nstate
character*64 cstate(nstate)initusr
subroutine should always be declared as
follows: character*64 cstate(nstate)cstate variable can be assigned the label to
print in the user-defined results with 1 being the index for the
first variable in the example
below: cstate(1) = “Variable Name for State(1)”Subroutine Arguments
| Argument | Type | Input / Output | Description |
|---|---|---|---|
idu |
integer | Input | This is defined via the USUBID parameter
on the MATUSHT Bulk Data Entry. This argument
can be used to define and choose between different types of
materials within the same user subroutine. optional use |
matID |
Integer | Input | Material ID. |
ieuid |
integer | Input | Element ID. |
|
Integer | Input | Gauss Integration Point. |
Layer |
Integer | Input | Laminate Layer. |
Simpson Point |
Integer | Input | Through-thickness Simpson Integration Point. |
drot(3,3) |
Double (table) | Input | Transformation matrix. |
props |
double (table) | Input | This table contains all the user-defined thermal material property information from the PROPERTY continuation line of the MATUSHT entry. |
nprops |
Integer | Input | This is the total number of thermal material properties defined on the PROPERTY continuation line of the MATUSHT entry. |
temp |
double | Input | This is the temperature at the end of the current increment. |
dtemp |
double | Input | This is the temperature increment of the current increment. |
kinc |
integer | Input | Current nonlinear increment. |
dt |
double | Input | Current time step increment |
t_step |
double | Input | Current subcase time of the current time step. |
t_total |
double | Input | Total time (if IC is used). This is effective when the IC case control entry of a nonlinear transient thermal subcase points to a previous nonlinear transient thermal subcase. |
Stater |
double (table) | Input | Table of State variables at the last converged time-step. They are constant between iterations of the same time step. |
State |
double (table) | Input/Output | Table of State variables at the current time-step. They are updated and passed between iterations of the same time-step. State variables are variables that can be requested as output in the H3D file. Any variable calculated within the solution process in the subroutine can be output by defining it as a state variable. |
nState |
integer | Input | Number of State Variables that the user requires in the
subroutine. See Stater for more
information. |
cstate |
string | Output | A character-based label from initusr
subroutine to OptiStruct. In the
usermaterial or smatusr
subroutines the state variables can be assigned user-defined
labels which can be displayed in the H3D
file when imported in HyperView. The
cstate variable provides the name for the
state variable declared in the subroutines to display in the
H3D file. |
hgen |
double (table) | Output | Scale factor for volumetric heat generation. For steady-state
analysis, the total power into an element referencing this
user-defined material with a constant volumetric heat generation
rate QVOL is: Pin = volume * HGEN * QVOL However, if QVOL is not applied to the element referencing this material, the internal heat generation calculated in the user subroutine is not applied to the element. |
smat |
Double (table) | Output | Material matrix. These are calculated during the solution and
are output to OptiStruct. Format for
smat matrix is provided below.
|
userdata |
Character | Output | User-defined message that is output based on the value of
ierr argument. |
ierr |
Integer | Input/Output | Flag that activates/deactivates Output message for an
OptiStruct run from the user
subroutine.
|
Output
Regular Built-in OptiStruct output, like Grid
Temperatures, Element Fluxes, and so on can be requested for any thermal material
user-subroutine based model. Additionally, user-defined output can also be requested
via the State(*) variable in the user-subroutine. The number of
such State(*) variables should be identified on the
NDEPVAR field.
This State variable can be assigned to any output variable that is required to be output from the subroutine, and it can then be visualized in HyperView after loading the H3D file.
Build External Libraries for User-defined Materials
You can build shared libraries on Windows or Linux.
Refer to Build External Libraries for more information.
Combined Hardening of von Mises Plasticity
Combining hardening can be used for analysis with cyclic loading, in order to capture shakedown, ratcheting effect, and so on.
It consists of two nonlinear hardening rules, the nonlinear kinematic (NLKIN) and nonlinear isotropic (NLISO) hardening methods.
Generally, the isotropic part is closely related to the von Mises criteria, and the kinematic part is described by the evolution law of back stress.
Combined hardening can be activated by setting HR=6 on the MATS1 Bulk Data.
Isotropic Hardening (NLISO): Nonlinear Yield Function
The yield function of von Mises plasticity can be expressed in a general form as:
- Deviatoric stress tensor.
- Back stress tensor.
- Yield stress as a function of equivalent plastic strain .
The flow rule is defined as change of plastic strain, expressed in rate form as:
Where, is the rate of plastic multiplier, which is also the rate of equivalent plastic strain.
The flow direction, can be introduced which is the derivative of the yield function with respect to the stress tensor,
Where, is the relative stress tensor, which is the difference between deviatoric stress and back stress.
For the nonlinear isotropic hardening, the yield stress is assumed to be a power law function of equivalent plastic strain:
Where, and are two parameters which can be directly input via the Q and B fields on the MATS1 data (HR=6, TYPISO=PARAM) or these parameters are computed by parameter fitting algorithms, based on the stress-strain curve from experiment. The isotropic part of the yield stress and the equivalent plastic stress are provided via the SIG and EPS fields on the MATS1 data (HR=6, TYPISO=TABLE).
Nonlinear isotropic hardening is based on the von Mises plasticity criteria and; therefore, is associated with the flow rule.
Kinematic Hardening (NLKIN): Evolution Law of Back Stress
Compared with traditional linear hardening (HR=1 or 2), or the mixed hardening (HR=3), the main difference of NLKIN via HR=6 is the extended evolution law of back stress, which consists of a set of evolution equations for each back stress component:
and
- Denotes the component number of the back stresses.
- Total number of back stress components.
- and
- Corresponding parameter pair of component .
As the evolution of back stress depends both on the flow direction that is parallel to and the back stress component itself; thus, the evolution law of back stress is non-associated. This leads to the unsymmetric elasto-plastic consistent tangent modulus. The unsymmetric solver is always turned on as long as combined hardening is active.
Time Integration Scheme
The plasticity problem is usually solved using the return mapping method, which means it is first assumed to be an elastic trial stage, and then the stress is pulled back onto the yield surface if plastic flow occurs. Backward-Euler algorithm is used during the return mapping process.
Parameter Fitting
If the stress-strain curve is provided (TYPKIN=HALFCYCL or TYPISO=TABLE), the data points provided are used to compute the optimal parameters for combined hardening. For parameter fitting, the Levenberg-Marquardt method is used, which is an extension of Newton method. The fitted parameters are printed in the .out file.
For NLISO with TYPISO=TABLE, the provided data in the continuation line is the yield stress versus equivalent plastic strain. This curve is usually generated based on the cyclic experiment with constant strain. The same curve is used for isotropic hardening (HR=1) for example, with TABLES1/TABLEG or TABLEST input.
Temperature-dependent combined hardening
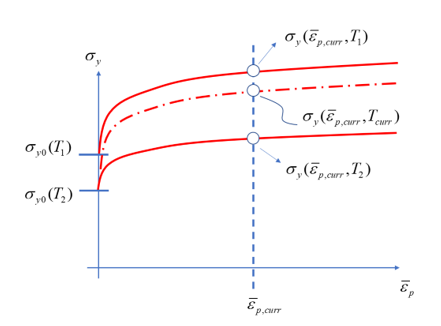
If temperature-dependent combined hardening is active, then all the parameters are temperature dependent, for example,
From experiment is only possible to test a limited number of temperatures. Interpolation is used to solving for plasticity at a temperature in between the test temperatures.
Using isotropic hardening NLISO as an example, if the parameters are provided at two temperatures and , then there are two yield stress functions for interpolation:
The interpolated yield stress at the current temperature in [ , ] is then,
with two factors for different temperatures , .
As an example, Figure 2 illustrates the principle of interpolation.
If the temperature, is beyond the available temperature range [ , ], then closest temperature will be selected. In other words, no extrapolation of temperature is performed. Furthermore, it is suggested to provide the material parameter of NLKIN and NLISO at the same temperature.
Cast Iron Plasticity
Cast iron material model is used to describe the yield behavior of grey cast iron, in which tension and compression behavior are different.
In this material model, rate form is used for strain evolution and the strain rate is decomposed into two parts (elastic and plastic parts) in an additive way.
Yield Function
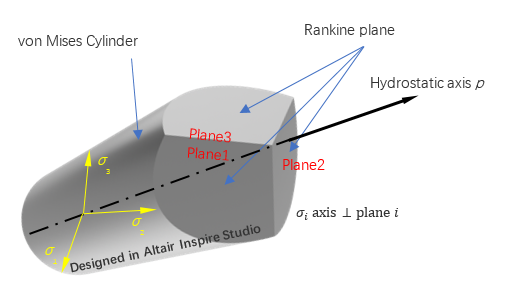
The yielding criteria is defined as:
Where,
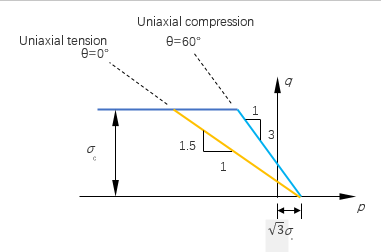
The first criterion is Rankine criterion (max. Principal stress criterion) for tensile yielding, and the second criterion is von Mises criterion for compressive yielding. Together they form a composite yield surface.
- Yield stress in uniaxial tension.
- Yield stress in uniaxial compression.
Since the material is assumed to be isotropic, the yield surface can be expressed with a function of three invariant measure of the stress tensor, , , and .
Where, is von Mises stress of a given stress state.
Where, is mean stress given by:
The invariant can be expressed as:
Where, is the tensor form of deviatoric stress.
The quantity is Lode’s Angle that is defined by and as shown below, which identifies the meridional plane for a given stress state.
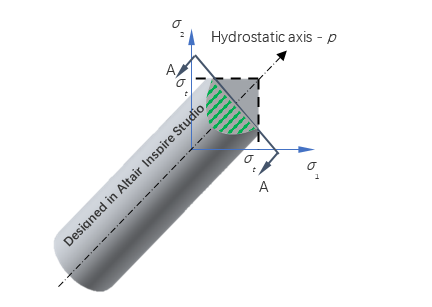
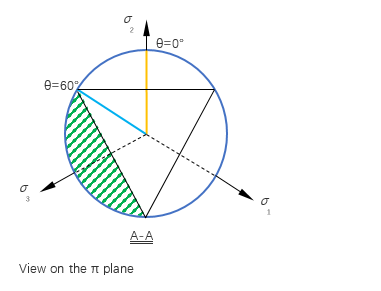
In the principal stress space, the yield function is a von Mises cylinder intersected with Rankine planes (Figure 3). The yield surface is illustrated in plane in Figure 4 and Figure 5, and in meridional plane in Figure 6.
Where, is the tensor form of deviatoric stress.
Flow Rule
The flow rule is expressed as:
Hardening Rule
In this material model, only isotropic hardening is considered. The yield strength is increasing as the equivalent plastic strain grows. It is noted that as tension and the compression have different flow rules, the equivalent plastic strain is different for tension and compression. Hence, the tensile yield strength and the compressive yield strength are looked up from the tensile and the compressive table separately.
The compressive equivalent plastic strain is expressed as:
Where, is the tensor of deviatoric part of plastic strain rate.
The tensile equivalent plastic strain is:
Where, .
In the above expressions, the subscript index implies the physical quantity is at time , and means the physical quantity is at the last converged time .
Input
Cast iron plasticity material data can be specified by using the MCIRON Bulk Data Entry which has the same identification number as an existing MAT1 Bulk Data Entry. The Tensile and Compressive stress-strain curves can be defined using the TABLE_T and TABLE_C fields on the MCIRON entry.
Cast iron material via MCIRON is supported for Small and Large Displacement Nonlinear Static Analysis and Nonlinear Transient Analysis. It is supported for CHEXA, CTETRA, CPENTA, and CPYRA elements (both first and second order).
In addition to regular result output, additional results from this material model are output if STRAIN(PLASTIC) I/O Option is specified. These results include, 6 plastic strain components, equivalent compressive plastic strain, equivalent tensile plastic strain, nodal results, and integration results are also available.
Multiscale Modeling
OptiStruct (OS) and Multiscale Designer (MDS) can be combined to perform multiscaling analysis on structural components utilizing both linear and nonlinear materials.
Heterogeneous materials such as composites, soil, solid foams, and polycrystals consist of one or more distinguishable constituents that have different mechanical properties. 12 For example, it is known that fiber-reinforced composite materials have a stiffer and stronger phase known as the reinforcement and, a less stiff and weaker phase known as the matrix. The governing equations are well understood in one of the scales, either the micro-scale or the macro-scale. While general constitutive equations are applicable to solids under deformation in the macro-scale, continuum models are required in the micro-scale. In order to bridge the gap between the two scales, you need to consider models at different scales simultaneously. This can be achieved by multiscaling techniques.
Classical laminate theory can predict the overall properties of heterogeneous laminates; whereas, homogenization theory provides information on the individual phase properties and phase geometries. Knowledge of individual phases is important to characterize material damage and failure. Hence, multiscaling techniques open unique opportunities for modeling by focusing the material behavior on different levels of physical laws.

- Unit cell geometry and mesh definition
- Linear material characterization
- Reduced-order homogenization
- Nonlinear material characterization
Single-scale Model
The basic steps required to construct a single-scale material model.
Cast iron plasticity is interesting to study because it has different yielding and hardening behavior when subjected to tensile and compressive loads. The first two sections explain the input data required from the Multiscale Designer (MDS). The next two sections explain the procedure to integrate the material in OptiStruct (OS) and perform structural analysis.
Linear Material Characterization
- isotropic
- trans-isotopic
- orthotropic
- anisotropic material
Here a homogeneous material with the properties of cast iron is utilized for characterization in the linear regime. The input elastic properties/parameters and values of the material are:
- Tensile Young’s modulus (GPa),
- 95.5
- Compressive Young’s modulus (GPa),
- 95.5
- Poisson's ratio,
- 0.26
Nonlinear Material Characterization
Various constitutive laws are available in Multiscale Designer, such as rate-independent plasticity, visco-elasticity, damage laws. Here isotropic damage – 3-piecewise Linear Evolution is used to simulate the nonlinear behavior of the material. The damage model formulation within Multiscale Designer follows the continuum damage mechanics framework. The elastic stiffness matrix is degraded by using a damage state variable which is a function of principal strains. Only for compressive loads, the principal strains are multiplied by a compression factor to alleviate the damage in compression. The compression factor is calculated internally, based on the input properties of the material.
- Stress at damage initiation – tension (MPa),
- 126.0
- Ultimate stress – tension (MPa),
- 210.3
- Strain at ultimate stress - tension,
- 0.008
- Strain to failure – tension,
- 0.008
- Stress at damage initiation – compression (MPa),
- 303.0
- Ultimate stress - compression (MPa),
- 443.3
- Strain at ultimate stress - compression,
- 0.010
- Strain to failure – compression,
- 0.010
Nonlinear material characterization is done with a Unnotched Tensile/Compression built-in macro simulation model. Two simulations are defined conforming to ASTM D3039, D3518 and D6641. One to simulate tensile behavior and one for compressive behavior. In the process, a unit mesh – solid cube is fixed on one end and subjected to x-direction displacement on the other end. The stresses are computed by extracting, the reaction forces divided by unit area.
- Loading rate – Tension (/s)
- 0.008
- Maximum strain - Tension
- 0.008
- Loading rate – Compression (/s)
- -0.01
- Maximum strain - Compression
- -0.01
The loading rate is the strain rate for the test. For all-rate independent laws (this includes isotropic damage law – 3 piecewise Linear evolution), it is typical to set the loading rate equal to the maximum strain. The minimum number of increments for mechanical loads is defined to be 20. This means that the initial time-step is set as the total step time divided by minimum mechanical increments.
The output data files are generated in the material model directory. The file path can be changed in the Multiscale Designer settings. The corresponding file names and descriptions are available in ‘Unit Cell Data Files’ of the Multiscale Designer User Manual.
Structural Analysis
Integrate Multiscale Designer Files with OptiStruct
- In Multiscale Designer, select the input file (.mic).
- Select the Solver Interfaces tab.
-
In the option for OptiStruct, click the
Multiscale Materials tab.
The Multiscale Designer solver interface for OptiStruct opens.
-
Make sure that the plugin “dll” and multiscale material
data files are pointing to the material subroutine and Multiscale Designer model, respectively.
Example directory to the material subroutine and Multiscale Designer model are <hwinstallation_directory\hwsolvers\MultiscaleDesigner\win64\plugins\optiStruct\umat.dll> and <working_directory\MultiscaleDesigner\model_name\Mechanical\model_name_mdsMAT.dat>, respectively.
The number of user-defined variables computed for isotropic damage law is 8, which the terms from damage state variable, equivalent strain, total strain, and Eigen strain.
-
Change the output folder directory for the plugin data to the model file path,
<working_directory\model_name\Mechanical>.
The generated plugin data file (OptiStruct_plugin_data.fem) contains the LOADLIB I/O and MATUSR cards for running the structural analysis. The LOADLIB I/O Entry is used to implement external subroutines and MATUSR is used to defined user material parameters and properties. These cards are later inserted into OptiStruct input model files (*.fem).
Note:- The input model file should be in the same folder as the multiscale material. The material subroutines are called into this database through LOADLIB.
- The USUBID number in the MATUSR should refer to the multiscale material model ID.
Single-scale Results
Sample cards are generated for Multiscale Designer-OptiStruct integration, with the results of tension and compression test in OptiStruct with the user-defined material.
Elastic properties from homogenization and stress-strain curve from damage law are presented.
Linear Material Characterization
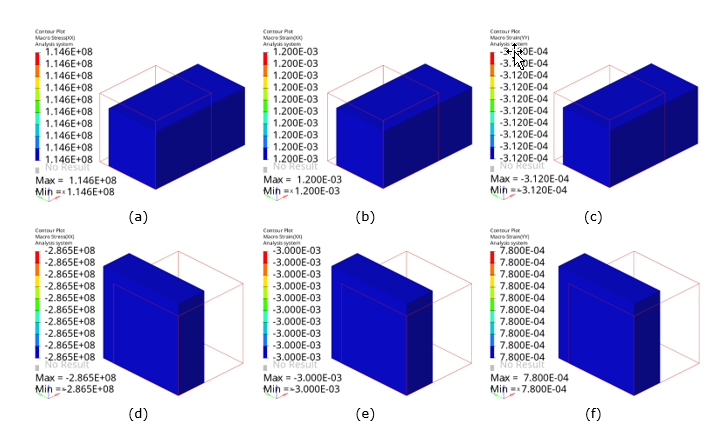
- Tensile Young’s modulus (GPa),
- 95.5
- Compressive Young’s modulus (GPa),
- 95.5
- Poisson's value,
- 0.26
Nonlinear Material Characterization
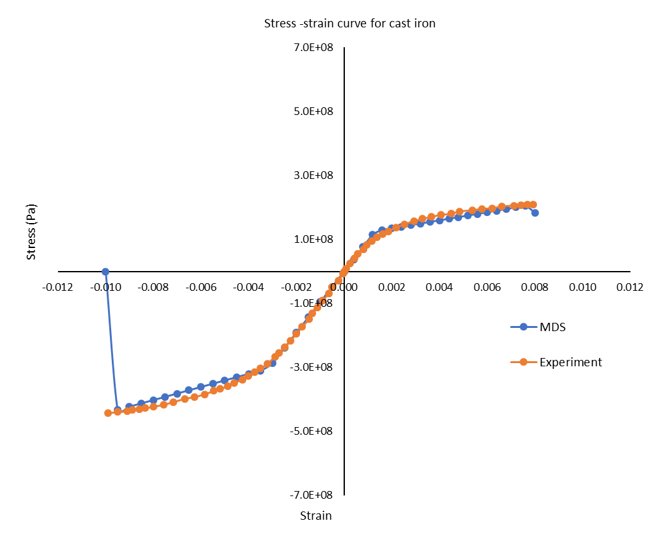
Multiscale Designer-OptiStruct Integration

Structural Analysis
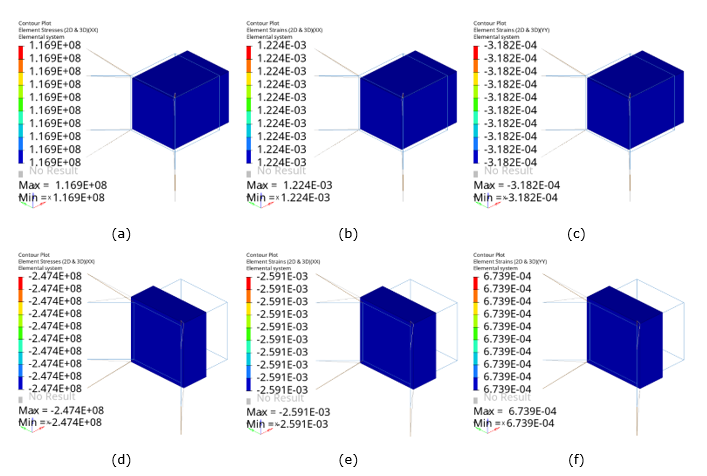
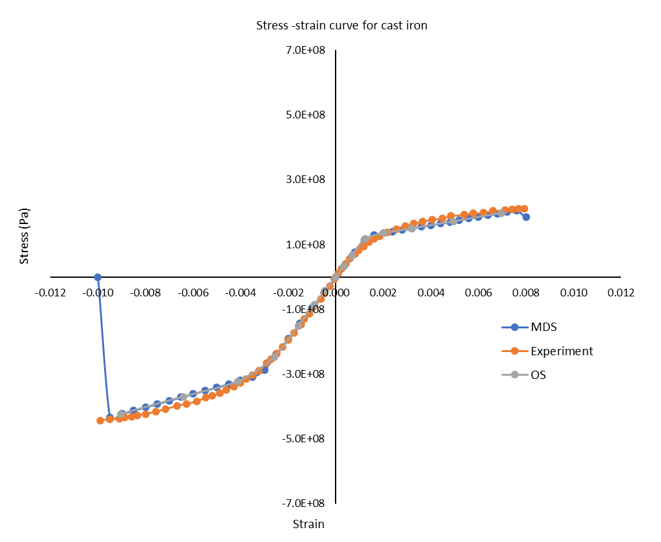
Multiscale Model
The basic steps required to construct a multiscale material model.
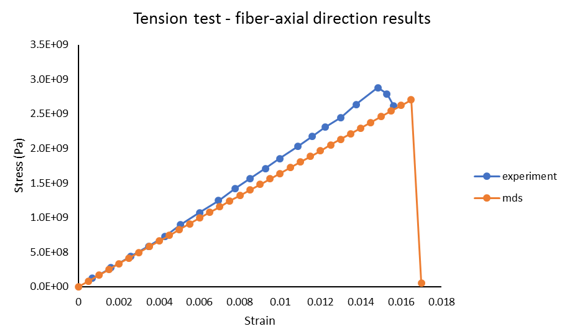
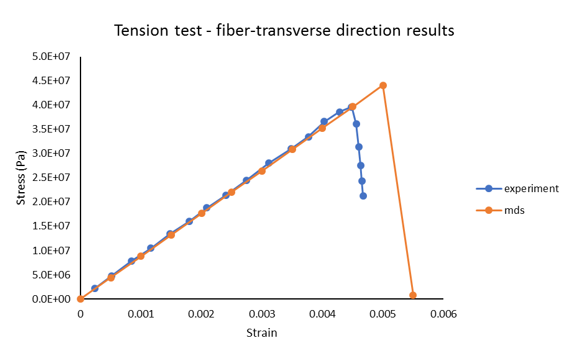
Unidirectional fiber-reinforced polymer composite is subjected to tensile load in fiber-axial and fiber-transverse directions. The response of the material is output and validated with experimental data. The first two sections explain the input data required from the Multiscale Designer (MDS). The next two sections explain the procedure to integrate the material in OptiStruct (OS).
Unit Cell Model and Linear Material Characterization
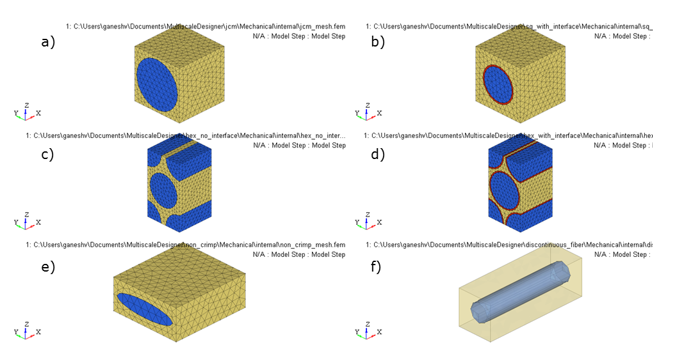
The matrix is modeled with homogeneous elastic properties and the fiber is assumed to be transversely isotropic. Periodic boundary conditions are applied to the unit cell to obtain the homogenized stiffness matrix of the composite.
- Young’s modulus of the matrix (GPa),
- 3.8
- Poisson’s ratio of the matrix,
- 0.32
- Longitudinal Young’s modulus of fiber (GPa),
- 252.25
- Transverse Young’s modulus of fiber (GPa),
- 13.45
- Longitudinal Poisson’s ratio,
- 0.02
- Transverse Poisson’s ratio,
- 0.3
Nonlinear Material Characterization
The matrix is assumed to obey isotropic damage – bilinear evolution model and the fiber is assumed to follow orthotropic damage – bilinear evolution, for simulating the nonlinear behavior of the material.
- Stress at damage initiation (MPa),
- 126.0
- Strain at ultimate stress,
- 0.1
- Stress at damage initiation – longitudinal direction (GPa),
- 4.2
- Strain at ultimate stress – longitudinal direction,
- 0.017
- Stress at damage initiation – transverse direction (MPa),
- 75.0
- Strain at ultimate stress – transverse direction,
- 0.05
For nonlinear material characterization in fiber-axial and fiber-transverse direction, two laminate layups with unit thickness are created with orientations 0° and 90°, respectively. Each laminate is subjected to Unnotched Tensile/Compression macro simulation with different loading rates.
- Loading rate – Fiber axial direction test (/s)
- 0.05
- Maximum strain - Fiber axial direction test
- 0.05
- Loading rate – Fiber transverse direction test (/s)
- 0.017
- Maximum strain - Fiber transverse direction test
- 0.017
The output data files are generated in the material model directory and the stress-strain curve data will export to an Excel spreadsheet file in <material_model_directory\model_name\mechanical\model_name_NLmatl.xlsx>.
Integrate Multiscale Designer Files with Multiscale Designer-OptiStruct
- In Multiscale Designer solver interface for OptiStruct, click the Homogenized Materials tab.
- Set the card images to MAT2, MAT8, MAT9 or MAT9ORT.
- Click the Multiscale Materials tab and set the output file path for the OptiStruct plugin “dll”.
-
In the multiscale material data file, browse the file path to
<material_model_directory\model_name\mechanical\model_name_mdsMAT.dat>.
The number of user-defined variables computed for orthotropic damage law is 8, which involves the terms from the damage state variable, equivalent strain, total strain, and eigen strain.
- By default, the OptiStruct plugin data files are output to <material_model_directory\Macro\Mechanical\optiStruct_plugin_data.fem>.
Multiscale Results
Sample cards are generated for Multiscale Designer-OptiStruct integration with OptiStruct test results.
Elastic properties from homogenization and stress-strain curve from damage law are presented.
Unit Cell Model and Linear Material Characterization

- Longitudinal Young’s modulus (GPa),
- 165.4
- Transverse Young’s modulus (GPa),
- 8.8
- Longitudinal Poisson’s ratio,
- 0.11
- Transverse Poisson’s ratio,
- 0.34
Nonlinear Material Characterization
Multiscale Designer-OptiStruct Integration