CQAXIG
Bulk Data Entry Defines a quadrilateral cross-section general axisymmetric element that allows circumferential deformation.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| CQAXIG | EID | PID | Theta | ||||||
| G1 | G2 | G3 | G4 | G5 | G6 | G7 | G8 |
Example
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| CQAXIG | 111 | 2 | 15.0 | ||||||
| 31 | 74 | 75 | 32 | 51 | 52 | 63 | 62 |
Definitions
| Field | Contents | SI Unit Example |
|---|---|---|
| EID | Unique element
identification number. No default (Integer > 0) |
|
| PID | A PAXIG entry identification
number. Default = EID (Integer > 0) |
|
| G1, G2, G3, G4 | Identification numbers of
corner grid points. No default (Integers > 0, all unique) |
|
| G5, G6, G7, G8 | Identification numbers to
edge grid points. No default (Integers > 0 or blank) |
|
| Theta | Material orientation angle in
degrees. Default = 0.0 (Real) |
Comments
- Element identification numbers must be unique with respect to all other element identification numbers.
- The property card entry to reference is PAXIG, which assigns the material and the axis-of-symmetry to the element.
- In comparison with 2d axisymmetric elements CQAXI and CTAXI (which have two degrees of freedom at each node), general axisymmetric elements have an additional degree of freedom at each node circumferentially; they can also have torsional deformation about the axis-of-symmetry.
- The grid ordering of
G1 through G8 is defined as shown in
Figure 1. All grids and the axis-of-symmetry must be on the same
plane, and the grids cannot span across the axis-of-symmetry on this plane.
Figure 1. CQAXIG Definition 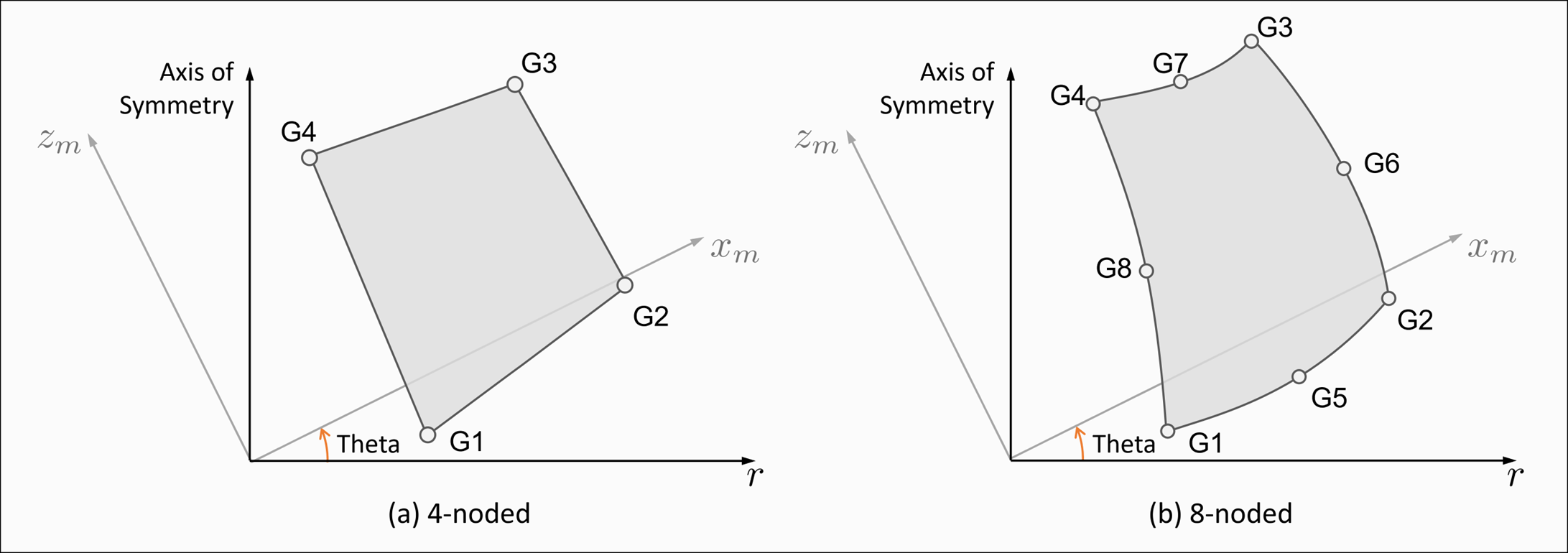
- If the PAXIG entry referenced in field 3 references a MAT3 entry, material properties and stresses are always given in the xm-zm coordinate system.
- A concentrated load (as in, the load
specified on a FORCE entry) at a grid Gi
of this element denotes that force applied onto the circumference with radius of
Gi. For example, to apply a load of 200 N/m on the
circumference at Gi located at a radius of 0.4 m, the
magnitude of the load specified on the static load entry is:
- General axisymmetric elements are supported in linear analyses (including static and dynamic analyses) and linear static preloading subcases.
- PARAM,AXI2DTOR,YES can be used to convert 2D axisymmetric elements CQAXI and CTAXI in the model to general axisymmetric elements CQAXIG and CTAXIG, respectively, while PAXI is considered as PAXIG.