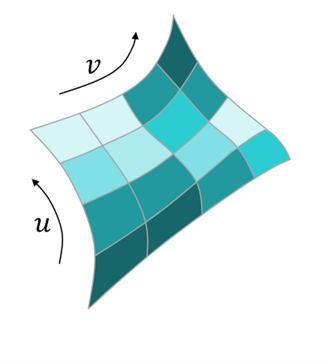
Lattice Design: Implicit Modeling vs. Traditional CAD

A comparison of designing lattices with implicit modeling versus traditional CAD.

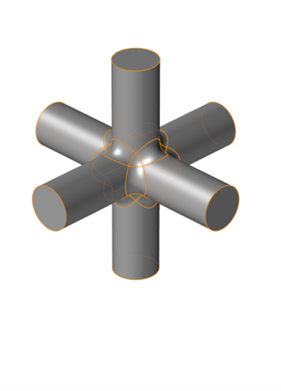
Lattice Design with Traditional CAD

When working with traditional CAD, creating boundary representation objects, a typical workflow for creating a lattice would look something like this:
  1. Construct a series of NURBS surface patches.
  2. Assemble these into a lattice unit cell.
  3. Then pattern that unit cell in 1-, 2-, or 3-dimensions to form a lattice.
Although this gives a tight control over the lattice geometry, this methodology does not scale well as the number of unit cells increases. You will quickly find that your CAD package is slowing down to the point of being unusable.
Figure 1. Parametric Surface Patches (e.g., NURBS)
Figure 2. Assemble Patches to Define a Unit Cell
Figure 3. Pattern the Unit Cell in 1, 2, or 3 Directions

Lattice Design with Implicit Modeling

Inspire’s implicit modeling approach uses a fundamentally different means of describing geometry to offer a suite of tools that enable you to create vastly more complex lattice structures or other high surface-area-to-volume ratio shapes.

Implicit modeling makes use of implicit surfaces. Implicit surfaces are perhaps best thought of as a field rather than a surface—at every point in space the field defines a scalar value, often some notional or actual distance to the nearest point on the surface. So, if we define the implicit surface as passing through all points in the field where the scalar values equal, say, zero, we call this surface the zero level-set of the field. The zero level-set can be computed and rendered as a single isosurface, which completely removes the need to compute and manage all of the watertight intersections that were present when stitching NURBS patches together. Another key point is that points on one side of the isosurface will have a positive scalar value, and points on the other will have negative scalar values. As such, we can run instant inside-outside checks for points in space, and we know how far away the surface is. This makes implicit modeling ideal for hardware acceleration on the GPU for both computation and rendering purposes.

Figure 4. Heat Map of a Field Slice. For every point in space, define a scalar value that represents the (notional) distance to the surface.
Figure 5. Implicit Isosurface. Construct a single implicit isosurface that passes through every point in space where the (notional) distance equals a defined constant.

In addition to significantly faster compute times, creating lattices using implicit modeling comes with some other very important benefits.

  1. In addition to strut lattices, which comprise nodes and struts between them, implicit modeling can also produce Surface Lattices, which are typically Triply Periodic Minimal Surfaces (TPMS), like a Gyroid. It is very difficult to accurately reproduce these using parametric surfaces, like NURBS.
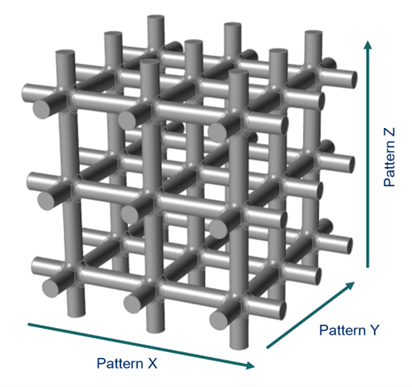
  2. Previously, regular lattices were created by copying and translating a unit cell of geometry in, say, the x-, y-, and z-directions (see image above). This means that there is no facility to smoothly increase the number of unit cells across the lattice. No such restriction applies in implicit modeling, where the number of unit cells can vary smoothly across the lattice structure, as below.

  3. It is possible to layer gradient effects using field-driven design. In the image below, the lattice experiences an decrease in relative density and unit cell size from left to right.

  4. It is even possible to combine lattice design with morph operations to smoothly transition from one lattice unit cell into another. The image below shows a Gyroid morphing into a Schwarz D lattice, moving from left to right.