/MAT/LAW2 (PLAS_JOHNS)

This model expresses material stress as a function of strain, strain rate and temperature. A built-in failure criterion based on the maximum plastic strain is available. For Solid and SPH elements, this material may account for the nonlinear dependence between pressure and density when corresponding Equation of State is prescribed.

Format

Definition

Comments

1. This is an elasto-plastic material model that includes strain rate and temperature effects with true stress and strain output.
2. In this model the material behaves as a linear-elastic material when the equivalent stress is lower than the plastic yield stress. For higher stress values, the material behavior is plastic, and the true stress is calculated as:
   $$\sigma =\left(a+b{{\epsilon }_p}^n\right)\left(1+c\ln \frac{\dot{\epsilon }}{{\dot{\epsilon }}_0}\right)\left(1-{(T^{\ast })}^m\right)$$
   Where,

   $T^{*}=\frac{T-T_r}{T_{melt}-T_r}$

   ${\epsilon }_p$

   Plastic strain

   $\dot{\epsilon }$

   Strain rate

   $T$

   Temperature

   T_r

   Ambient temperature

   T_melt

   Melting temperature

3. If I_flag=0, the Johnson-Cook equation parameters a, b, and n values are entered.

   If I_flag=1, experimental engineering stress and stain data can be entered for ${\sigma }_y$ , UTS and ${\epsilon }_{UTS}$ and the parameters a, b and n are calculated and printed in the Starter output file. If the a, b and n parameters cannot be automatically fit, then a Starter warning message will contain important information about changes to the material input.

4. The plastic yield stress should always be greater than zero. To model pure elastic behavior, the plastic yield stress should be set to 10²⁰.
5. When ${\epsilon }_p$ reaches the value of ${\epsilon }_p^{max}$ in one integration point, then based on the element type:
   • Shell elements: The corresponding shell element is deleted.
   • Solid elements: The deviatoric stress of the corresponding integral point is permanently set to 0; however, the solid element is not deleted.
6. The plastic hardening exponent, n must be less than or equal to 1.
7. The strain rate has no effect on truss elements.
8. To eliminate the effect of the strain rate, you can either set the value of c equal to 0 or the reference strain rate ( ${\dot{\epsilon }}_0$ ) can be set equal to 10²⁰. There is no effect of strain rate when $\dot{\epsilon }$ is less than ${\dot{\epsilon }}_0$ .
9. The ICC flag defines the effect of strain rate on the maximum material stress ${\sigma }_{\max }$ . Figure 1 shows the value of for ${\sigma }_{\max }$ the corresponding ICC flag.

   

   $\sigma =\left(a+b{{\epsilon }_p}^n\right)\left(1+c\ln \left(\frac{\dot{\epsilon }}{{\dot{\epsilon }}_o}\right)\right)$	$\sigma =\left(a+b{{\epsilon }_p}^n\right)\left(1+c\ln \left(\frac{\dot{\epsilon }}{{\dot{\epsilon }}_o}\right)\right)$
   ${\sigma }_{\max }={\sigma }_{\max 0}\left(1+c\ln \left(\frac{\dot{\epsilon }}{{\dot{\epsilon }}_o}\right)\right)$	${\sigma }_{\max }={\sigma }_{\max 0}$

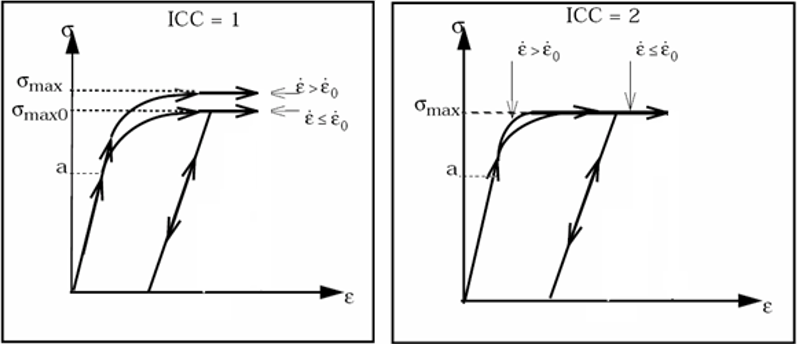
10. There is no effect of temperature on trusses. Beam element (with /PROP/TYPE3 or /PROP/TYPE18) together with /HEAT/MAT or /THERM_STRESS/MAT could consider thermal effect.
11. The temperature is constant ( $T=T_r$ ), if $\rho C_p=0$ .
12. Adiabatic conditions are assumed for thermal simulations with initial temperature equal to reference temperature (T_r) and:
    $$T=T_r+\frac{Q}{\rho C_p\left(Volume\right)}$$

    Where, $Q=\Sigma \text{Δ}E$ is the plastic energy increment with $\text{Δ}E=\sigma ·\delta {\epsilon }_p$ .

13. The strain rate coefficient, c and reference strain rate ${\dot{\epsilon }}_0$ must be defined to include thermal effects.
14. When /HEAT/MAT (with I_form=1) references this material model, the values of T_r, T_melt and $\rho C_p$ defined in this card will be overwritten by the corresponding $T_0$ , $T_1$ and $\rho {}_0{C}_p$ defined in /HEAT/MAT.
15. When the temperature is not initialized using /HEAT/MAT or /INITEMP, the reference temperature (T_r) is also the initial temperature.
16. The hardening coefficient is used to describe the hardening model (during unloading). The values of the hardening coefficient should be between 0 and 1.
17. By default, the hydrostatic pressure is linearly proportional to the density:
    $$P=K\mu$$
    Where,

    $K=\frac{E}{3\left(1-2v\right)}$

    Bulk modulus

    $\mu =\frac{V_0}{V}-1=\frac{\rho }{{\rho }_0}-1$

    An additional Equation of State (/EOS) card can refer to this material in order to define a nonlinear dependency between hydrostatic pressure and volumetric strain.

    This behavior is only available for solid and SPH elements.