/MAT/LAW104 (JOHNS_VOCE_DRUCKER)

Block Format Keyword An elasto-plastic constitutive material law using the 6^th order Drucker model with a mixed Voce and linear hardening.

Dependence on the Johnson-Cook strain rate and thermal softening effects due to self-heating can also be modeled. The law is available for isotropic shell and solid elements.

Format


(1)	(3)	(5)	(7)	(9)
/MAT/LAW104/`mat_ID`/`unit_ID` or /MAT/JOHNS_VOCE_DRUCKER/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$
`E`	$v$	`I`_res
$σ_{y l d}^{0}$	`H`	`Q`	`B`	`C`_DR
`C`_JC	${\dot{ε}}_{0}$	`Fcut`
$μ$	`T`_ref	`T`_ini
$η$	`C`_p	${\dot{ε}}_{i s o}$	${\dot{ε}}_{a d}$

Definition


Field	Contents	SI Unit Example
`mat_ID`	Material identifier. (Integer, maximum 10 digits)
`unit_ID`	(Optional) Unit identifier. (Integer, maximum 10 digits)
`mat_title`	Material title. (Character, maximum 100 characters)
$ρ_{i}$	Initial density. (Real)	$[\frac{kg}{m^{3}}]$
`E`	Young‘s modulus. (Real)	$[Pa]$
$v$	Poisson’s ratio. (Real)
`I`_res	Resolution method for plasticity. = 0 Set to 1. = 1 (Default) NICE (Next Increment Correct Error) explicit method. = 2 Newton iterative implicit method. (Integer)
$σ_{y l d}^{0}$	Initial yield stress. (Real)	$[Pa]$
`H`	Linear hardening module. (Real)	$[Pa]$
`Q`	Voce hardening coefficient. (Real)	$[Pa]$
`B`	Voce hardening exponent. (Real)
`C`_DR	Drucker coefficient. (Real)
`C`_JC	Johnson-Cook strain rate coefficient. (Real)
${\dot{ε}}_{0}$	Inviscid limit for the plastic strain rate. (Real)	$[\frac{1}{s}]$
`Fcut`	Plastic strain rate filtering frequency. Default = 10 kHz (Real)	$[\frac{1}{s}]$
$μ$	Temperature softening slope. (Real)	$[\frac{1}{K}]$
`T`_ref	Reference temperature at which the hardening law was identified in experiment. (Real)	$[K]$
`T`_ini	Initial temperature of material in simulation. (Real)	$[K]$
$η$	Taylor-Quinney coefficient. (Real)
`C`_p	Specific heat. (Real)	$[\frac{J}{kg \cdot K}]$ .
${\dot{ε}}_{i s o}$	Plastic strain rate at isothermic conditions. (Real)	$[\frac{1}{s}]$
${\dot{ε}}_{a d}$	Plastic strain rate at adiabatic conditions. (Real)	$[\frac{1}{s}]$

Comments

The law uses 6^th order Drucker equivalent stress definition:
$σ_{e q} = k {(J_{2}^{3} - C_{D R} J_{3}^{2})}^{\frac{1}{6}}$
Where, $J_{2}$ , $J_{3}$ are respectively the second and third invariant of the deviatoric stress tensor $k = {(\frac{1}{27} - C_{D R} \frac{4}{27^{2}})}^{- \frac{1}{6}}$ .
The parameter is user-defined and allows to define several yield surfaces (Figure 1). To respect the convexity, its value must respect -27/8 ≤ C_DR ≤ 2.25.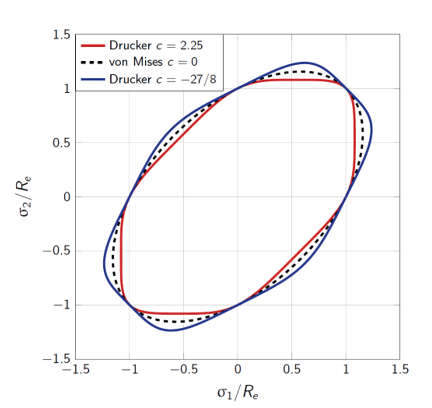
Figure 1. Drucker yield surfaces
The yield function is defined as:
$ϕ = \frac{σ_{e q}^{2}}{σ_{y l d}^{2}} - 1 = 0$
and
$σ_{y l d} = (σ_{y l d}^{0} + H ε_{p} + Q (1 - e^{- B ε_{p}})) (1 + C_{J C} ln (\frac{{\dot{ε}}_{f}}{{\dot{ε}}_{0}})) (1 - μ (T - T_{r e f}))$
Where,

$σ_{y l d}^{0}$

Initial yield stress.

H

Linear hardening.

$Q, B$

Voce hardening parameters.

$C_{J C}$

Johnson-Cook strain rate coefficient.

${\dot{ε}}_{f}$

Filtered plastic strain-rate.

Refer to Filtering in the User Guide.

${\dot{ε}}_{0}$

Inviscid limit plastic strain rate.

$μ$

Thermal softening slope.

The evolution of this flow stress equation with plasticity.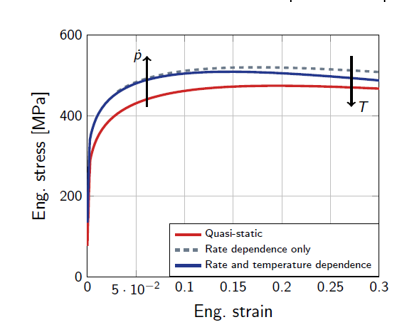
Figure 2. Flow stress evolution with plasticity
If /HEAT/MAT is not used for this material, the temperature is calculated internally using the incremental formula:
$d T = ω ({\dot{ε}}_{p}) \frac{η}{C_{p}} d W_{p}$
Where,

$d W_{p}$

Plastic work increment.

$η$

Taylor-Quinney coefficient that must respect $0 \leq η \leq 1$ .

$ω ({\dot{ε}}_{p})$

Coefficient that defines the transition between isothermal and adiabatic conditions (Figure 3).

$ω (\dot{ε_{p}}) = \frac{{({\dot{ε}}_{p} - {\dot{ε}}_{i s o})}^{2} (3 {\dot{ε}}_{a d} - 2 {\dot{ε}}_{p} - {\dot{ε}}_{i s o})}{{({\dot{ε}}_{a d} - {\dot{ε}}_{i s o})}^{3}}$
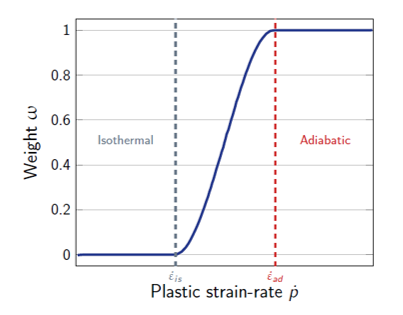
Figure 3. Evolution of the temperature weight with the plastic strain rate