/MAT/LAW76 (SAMP)
Block Format Keyword This law describes a semi-analytical elasto-plastic material using user-defined functions for the work-hardening portion for tension, compression and shear (stress as function of strain).
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /MAT/LAW76/mat_ID/unit_ID or /MAT/SAMP/mat_ID/unit_ID | |||||||||
| mat_title | |||||||||
| E | |||||||||
| tab_IDt | tab_IDc | tab_IDs | |||||||
| Fscalet | Fscalec | Fscales | XFAC | ||||||
| fct_IDpr | Fscalepr | Fsmooth | Fcut | ||||||
| fct_ID1 | Fscale1 | ||||||||
| Iform | IQUAD | ICONV | |||||||
Definition
| Field | Contents | SI Unit Example |
|---|---|---|
| mat_ID | Material
identifier. (Integer, maximum 10 digits) |
|
| unit_ID | Unit Identifier. (Integer, maximum 10 digits) |
|
| mat_title | Material
title. (Character, maximum 100 characters) |
|
| Initial
density. (Real) |
||
| E | Initial Young's
modulus. (Real) |
|
| Poisson's
ratio. (Real) |
||
| tab_IDt | Tension yield stress table
identifier (stress versus plastic tension strain with the
possibility of strain rate dependency). (Integer) |
|
| tab_IDc | Compression yield stress
table identifier (stress versus plastic compression strain with the
possibility of strain rate dependency). (Integer) |
|
| tab_IDs | Shear yield stress table
identifier (stress vs. plastic shear strain with the possibility of
strain rate dependency). (Integer) |
|
| Fscalet | Scale factor for ordinate
(stress) for
tab_IDt. Default = 1.0 (Real) |
|
| Fscalec | Scale factor for ordinate
(stress) for
tab_IDc. Default = 1.0 (Real) |
|
| Fscales | Scale factor for ordinate
(stress) for
tab_IDs. Default = 1.0 (Real) |
|
| XFAC | Scale factor for the
second entry (strain rate) of the three tables
(tab_IDt,
tab_IDc, and
tab_IDs). 6 Default = 1.0 (Real) |
|
| Plastic Poisson's
ratio. (Real) |
||
| fct_IDpr | Plastic Poisson's ratio
function identifier (
versus plastic
strain). (Real) |
|
| Fscalepr | Scale factor for ordinate (
) in
fct_IDpr. Default = 1.0 (Real) |
|
| Fsmooth | Smooth strain rate option flag.
(Integer) |
|
| Fcut | Cutoff frequency for
strain rate filtering. Default = 1030 (Real) |
|
| Failure plastic strain
(start of element damage). Default = 2e30 (Real) |
||
| Maximum plastic strain
(element deleted). Default = 2e30 (Real) |
||
| fct_ID1 | Damage function identifier
(damage versus plastic strain). 2 (Integer) |
|
| Fscale1 | Scale factor for ordinate
for fct_ID1. 2 Default = 1.0 (Real) |
|
| Iform | Formulation flag. 4
(Integer) |
|
| IQUAD | Yield surface flag. 3
(Integer) |
|
| ICONV | Convexity condition flag.
(Integer) |
Example (Material)
#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
kg mm ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW76/1/1
LAW76_Material
# RHO_I
1E-6
# E nu
100.0 .3
# TAB_IDt TAB_IDc TAB_IDs
1000 1001 1003
# Fscale_t Fscale_c Fscale_s XFAC
1.000 1.000 1.000 1.000
# Nu_p fct_IDpr Fscale_pr Fsmooth Fcut
0.5 0 0 1 1e30
# EPS_f_p EPS_r_p
0 0
#funct_ID1 Fscale_1
0
# IFORM IQUAD ICONV
0 0 1
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/TABLE/1/1000
curve_list TENSION strain rates
2
10010 1.0e-4
10020 1.0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/10010
eps_vs_sigma funct dt=1.0e-4
0.0000 .100000
1.0000 .200000
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/10020
eps_vs_sigma funct dt=1.0e-4
0.0000 .100000
1.0000 .200000
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/TABLE/1/1001
curve_list COMPRESSION strain rates
2
10030 1.0e-4
10040 1.0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/10030
eps_vs_sigma funct dt=1.0e-4
0.0000 .200000
1.0000 .400000
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/10040
eps_vs_sigma funct dt=1.0e-4
0.0000 .200000
1.0000 .400000
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/TABLE/1/1003
curve_list SHEAR strain rates
2
10050 1.0e-4
10060 1.0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/10050
eps_vs_sigma funct dt=1.0e-4
0.0000 .050000
0.5000 .060000
1.0000 .065000
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/10060
eps_vs_sigma funct dt=1.0e-4
0.0000 .050000
0.5000 .060000
1.0000 .065000
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/ENDComments
- This material is compatible with shell, thick shell and solid elements.
- The material damage can be
modeled two ways:
- (start to damage) and (element delete)
- Damage function fct_ID1
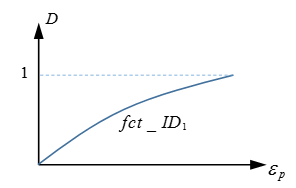
If damage function fct_ID1 is used, then and will be ignored.
- Choice of yield surface:
(1) Where,(2) (3) , and coefficients are computed from the hardening curve given for tension, compression and shear.
For von Mises and Drucker-Prager yield surface, IQUAD=0 can be used. However, in some situations, it can be difficult for Radioss to fit the , and coefficients when using IQUAD=0 and an easier fit is obtained by using IQUAD=1.
- Choice of plasticity
formulation:
- For the no associated plasticity formulation, Iform=0:
The plastic flow rule function, , is used to describe plastic strain increment . In this case is not normal to the yield surface and is not associated with the yield surface .
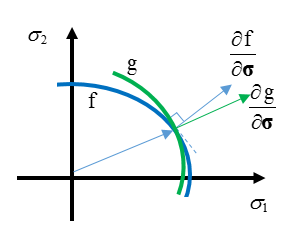
Figure 1.The plastic flow rule, , is given by:(4) Materials like soil or rock usually use the no associated plasticity formulation, Iform=0.
- For the associated plasticity: Iform= 1,
In this case, the plastic strain rate is a function of the normal vector of the yield surface . Materials like metal usually use the associated plasticity formulation.
(5) 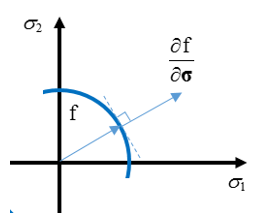
Figure 2.
- For the no associated plasticity formulation, Iform=0:
- The convexity condition flag ICONV=1 is used to ensure stability in the material law by making sure the yield surface is convex. The yield surface may be hyperbolic for low shear yield values in tension and compression. In this case there is no unique solution and Radioss will update (increase) the shear yield stress to ensure convexity of the yield surface. Therefore, the shear yield stress may be different from input curve.
- The tables should have a maximum dimension equal to 2. The first entry is the plastic strain and the second entry is the strain rate.
- User variables USR2, USR3, USR4 are used to output plastic strain components in tension, compression and shear. The output is available both for shells and solids in time history and in animation file.