/MAT/LAW115 (DESHFLECK)
Block Format Keyword An elasto-plastic constitutive law using von Mises criterion with pressure dependence. The hardening law is linear – nonlinear with an increasing exponential hardening.
Parameters can either be constant over all element of the part or can be statistically distributed over the elements. This introduces a probabilistic approach in the results of the simulation.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /MAT/LAW115/mat_ID/unit_ID or /MAT/DESHFLACK/mat_ID/unit_ID | |||||||||
| mat_title | |||||||||
| E | Ires | Istat | |||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
Definition
| Field | Contents | SI Unit Example |
|---|---|---|
| mat_ID | Material identifier. (Integer, maximum 10 digits) |
|
| unit_ID | Optional: Unit
identifier. (Integer, maximum 10 digits) |
|
| mat_title | Material title. (Character, maximum 100 characters) |
|
| Initial
density. (Real) |
||
| E | Young‘s
modulus. (Real) |
|
| Poisson's
ratio. (Real) |
||
| Ires | Resolution method for plasticity.
(Integer) |
|
| Istat | Activate statistical variation
flag.
(Integer) |
|
| Yield surface shape
parameter. Default = 0.0 (Real) |
||
| Linear hardening modulus. Default = 0.0 (Real) |
||
| Densification strain. Default = 1.0E20 (Real) |
||
| Nonlinear hardening
modulus. Default = 0.0 (Real) |
||
| Nonlinear hardening
parameter. Default = 1.0 (Real) |
||
| Initial flow stress. Default = 1.0E20 (Real) |
||
| Tensile volumic plastic strain at
failure. Default = 0.0 (Real) |
||
| Maximum principal stress at
failure. Default = 0.0 (Real) |
||
| Density of base material (matrix
material of the foam). Default = 1.0E20 (Real) |
||
| , | Statistical law parameters for
initial flow stress. (Real) |
|
| , | Statistical law parameters for
nonlinear hardening modulus. (Real) |
|
| , | Statistical law parameters for
linear hardening modulus. (Real) |
|
| , | Statistical law parameters for
nonlinear hardening exponent inverse. (Real) |
|
| Statistical law exponent of the
parameter. (Real) |
Example (Aluminum)
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/25
Local unit system
Mg mm s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW115/1/25
Aluminum foam constant
# Init. dens.
5.1E-10
# E Nu Ires Istat
5562.0 0.3 2 0
# ALPHA EPSVP_F SIGP_F
2.12 0.11 32.1
# SIGP GAMMA EPSD ALPHA2 BETA
14.82 5.37 1.67 66.9 2.99
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#enddataExample (Random Noise/Distribution)
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/25
Local unit system
Mg mm s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/DESHFLECK/1/25
Aluminum foam statistical
# Init. dens.
5.1E-10
# E Nu Ires Istat
5562.0 0.3 1 1
# ALPHA EPSVP_F SIGP_F RHOF0
2.12 0.11 30.0 2.7E-9
# SIGP_C0 SIGP_C1 SIGP_N
0 590.0 2.21
# ALPHA2_C0 ALPHA2_C1 ALPHA2_N
0 140.0 0.45
# GAMMA_C0 GAMMA_C1 GAMMA_N
0 40.0 1.4
# INV_BETA_C0 INV_BETA_C1 INV_BETA_N
0.22 320.0 4.66
/PERTURB/PART/SOLID/1
set Random Noise with random distribution on Solid density
# Mean_value Deviation Min_cut Max_cut Seed Idistri
1.0 0.02471 0.6 1.4 1000 2
#grpart_ID parameter
46 DENS
/GRPART/PART/46
part
1
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#enddataComments
- The material is supposed to be isotropic linear elastic.
- The law uses the
Deshpande-Fleck equivalent stress definition:
(1) Where,- The von Mises equivalent stress.
- The mean stress defined by:
(2)
The parameter controls the effect of pressure dependence in the computation of equivalent stress. This parameter must respect the following inequality:(3) - The yield
function is denoted
, compared to the Deshpande-Fleck equivalent
stress to the flow stress,
:
(4) With the flow stress defined by (Figure 1):(5) Where,- Initial flow stress.
- Linear hardening modulus.
- Densification strain.
- Nonlinear hardening modulus.
- Nonlinear hardening exponent.
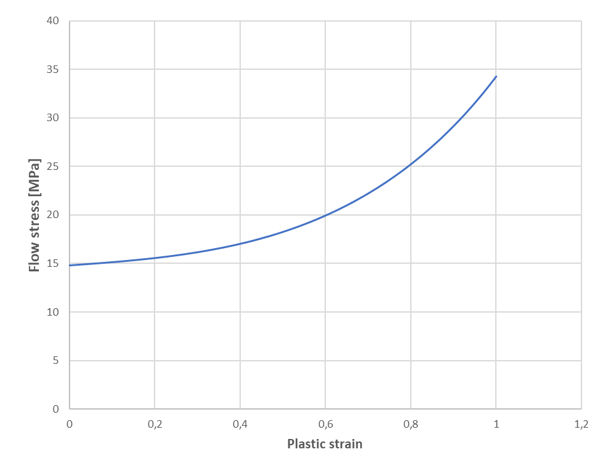
Figure 1. Flow stress evolution with plastic strain - Two versions of
the same material are available, depending on the value of the flag
Istat:
- If Istat = 0: parameters , , , and are the same for all solid elements of the part.
- If
Istat =
1: parameters
,
,
,
and
are not the same for all solid elements of
the part.They are computed from the foam density that is statistically distributed (using /PERTURB/PART/SOLID).
(6) Where,- , , and
- Statistical law parameters.
- Base material density (for instance, if the material law represents aluminum foam, will be aluminum density).
- When using
Istat =
1, the card /PERTURB/PART/SOLID must
be set to create the initial foam density
distribution over all elements of the part (Figure 2).

Figure 2. Example: foam density distribution in a foam block for an impact simulation - Most failure criteria are compatible with /MAT/LAW115; however, element deletion can be onset by you, if and/or are different from 0. The element deletion will be onset if the tensile volumetric strain is higher than and/or, if the first principal stress is higher than .