/MAT/PLAS_ZERIL
Block Format Keyword This law defines an isotropic elasto-plastic material using the Zerilli-Armstrong plasticity model.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /MAT/PLAS_ZERIL/mat_ID/unit_ID | |||||||||
| mat_title | |||||||||
| E | v | VP | |||||||
| C0 | C5 | n | |||||||
| C1 | ICC | Fsmooth | Fcut | ||||||
| C3 | C4 | Tr | |||||||
Definition
| Field | Contents | SI Unit Example |
|---|---|---|
| mat_ID | Material
identifier. (Integer, maximum 10 digits) |
|
| unit_ID | Unit Identifier. (Integer, maximum 10 digits) |
|
| mat_title | Material
title. (Character, maximum 100 characters) |
|
| Initial
density. (Real) |
||
| E | Young's
modulus. (Real) |
|
| v | Poisson's
ratio. (Real) |
|
| VP | Formulation for rate effects.
(Integer) |
|
| C0 | Plasticity yield
stress. (Real) |
|
| C5 | Plasticity hardening
parameter. (Real) |
|
| n | Plasticity hardening
exponent. 5 Default = 1.0 (Real) |
|
| Failure plastic
strain. Default = 1030 (Real) |
||
| Plasticity maximum
stress. Default = 1030 (Real) |
||
| C1 | Strain rate formulation
coefficient. (Real) |
|
| Reference strain rate
(must be 1 s-1 converted into user's
units). (Real) |
||
| ICC | Strain rate computation
flag. 7
(Integer) |
|
| Fsmooth | Smooth strain rate option flag.
(Integer) |
|
| Fcut | Cutoff frequency for
strain rate filtering. 8 Default = 1030 (Real) |
|
| C3 | Temperature effect
coefficient. (Real) |
|
| C4 | Temperature effect coefficient.
(Real) |
|
Specific heat per unit of volume.
(Real) |
||
| Tr | Reference
temperature. Default = 298 K (Real) |
Comments
- The Zerilli-Armstrong law is applicable only to shells and solids.
- The equation that describes
stress during plastic deformation is:
(1) Where,- Plastic strain
- Strain rate
- Temperature
- Yield stress should be strictly positive.
- When
reaches
in one integration point, then based on the element
type:
- Shell elements:
The corresponding shell element is deleted.
- Solid elements:
The deviatoric stress of the corresponding integral point is permanently set to 0; however, the solid element is not deleted.
- Shell elements:
- n must be less than 1.
- If is 0, there is no strain rate effect.
- ICC is a flag of the strain rate
effect on material maximum stress
:
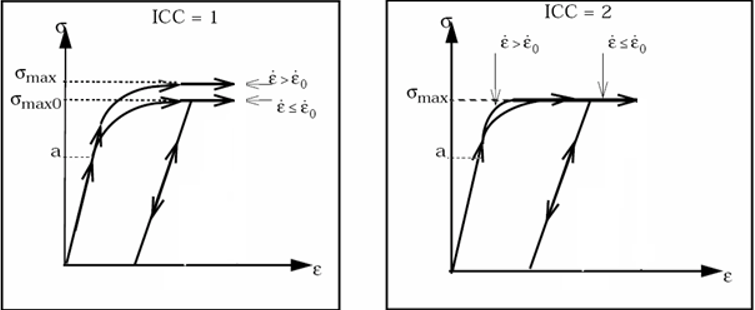
Figure 1. - Strain rate filtering input (Fcut) is only available for shell and solid elements.
- The strain rate filtering is used to smooth strain rates.
- Temperature is computed
assuming adiabatic conditions:
(2) Where, Eint is the internal energy computed by Radioss.
- When the temperature is not initialized using /HEAT/MAT or /INITEMP, the reference temperature (Tr) is also the initial temperature.