/MAT/LAW4 (HYD_JCOOK)

Block Format Keyword This law represents an isotropic elasto-plastic material using the Johnson-Cook material model. This model expresses material stress as a function of strain, strain rate and temperature.

This material may account for the nonlinear dependence between pressure and volumetric strain when corresponding equation of state is specified. A built-in failure criterion based on the maximum plastic strain is available. This material law is compatible with solid elements only.

Format


(1)	(3)	(5)	(7)	(9)
/MAT/LAW4/`mat_ID`/`unit_ID` or /MAT/HYD_JCOOK/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$ $ρ_{i}$	$ρ_{0}$ $ρ_{0}$
`E`	$ν$ $ν$
`a`	`b`	`n`	$ε_{p}^{m a x}$ $ε_{p}^{m a x}$	$σ_{\max}$ $σ_{\max}$
`P`_min
`c`	${\dot{ε}}_{0}$ ${\dot{ε}}_{0}$	`m`	`T`_melt	`T`_max
$ρ_{0} C_{p}$ $ρ_{0} C_{p}$			`T`_r

Definition


Field	Contents	SI Unit Example
`mat_ID`	Material identifier. (Integer, maximum 10 digits)
`unit_ID`	Unit identifier. (Integer, maximum 10 digits)
`mat_title`	Material title. (Character, maximum 100 characters)
$ρ_{i}$ $ρ_{i}$	Initial density. (Real)	$[\frac{kg}{m^{3}}]$ $[\frac{kg}{m^{3}}]$
$ρ_{0}$ $ρ_{0}$	Reference density used in E.O.S (equation of state). Default = $ρ_{0} = ρ_{i}$ $ρ_{0} = ρ_{i}$ (Real)	$[\frac{kg}{m^{3}}]$ $[\frac{kg}{m^{3}}]$
`E`	Young's modulus. (Real)	$[Pa]$ $[Pa]$
$ν$ $ν$	Poisson's ratio. (Real)
`a`	Yield stress. (Real)	$[Pa]$ $[Pa]$
`b`	Plastic hardening parameter. (Real)	$[Pa]$ $[Pa]$
`n`	Plastic hardening exponent. Default = 1.0 (Real)
$ε_{p}^{m a x}$ $ε_{p}^{m a x}$	Failure plastic strain. Default = 10³⁰ (Real)
$σ_{\max}$ $σ_{\max}$	Maximum stress. Default = 10³⁰ (Real)	$[Pa]$ $[Pa]$
`P`_min	Pressure cutoff ( < 0 ). Default = -10³⁰ (Real)	$[Pa]$ $[Pa]$
`c`	Strain rate coefficient. = 0 No strain rate effect. Default = 0.00 (Real)
${\dot{ε}}_{0}$ ${\dot{ε}}_{0}$	Reference strain rate. If $\dot{ε} \leq {\dot{ε}}_{0}$ $\dot{ε} \leq {\dot{ε}}_{0}$ , no strain rate effect. (Real)	$[\frac{1}{s}]$ $[\frac{1}{s}]$
`m`	Temperature exponent. Default = 1.00 (Real)
`T`_melt	Melting temperature. = 0 No temperature affect. Default = 10³⁰ (Real)	$[K]$ $[K]$
`T`_max	For `T` > `T`_max: `m` = 1 is used. Default = 10³⁰ (Real)	$[K]$ $[K]$
$ρ_{0} C_{p}$ $ρ_{0} C_{p}$	Specific heat per unit volume. (Real)	$[\frac{J}{m^{3} \cdot K}]$ $[\frac{J}{m^{3} \cdot K}]$
`T`_r	Reference temperature. Default = 300K (Real)	$[K]$ $[K]$

▸Example (Aluminum)

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
                   g                  cm                 mus
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/HYD_JCOOK/1/1
Aluminum
#              RHO_I               RHO_0              
                 2.8                   0                   
#                 E                   nu
                .734                 .33
#                  A                   B                   n              epsmax              sigmax
               .0024               .0042                  .8                   0               .0068
#               Pmin
              -.0223
#                  C           EPS_DOT_0                   M               Tmelt               Tmax
                .062                1E-6                   1                1220                   0
#              RHOCP                                                         T_r
             2.59E-5                                                           0
/EOS/TILLOTSON/1/1
Aluminum
#                 C1                  C2                   A                   B
                .752                 .65                  .5                1.63
#                 ER                  ES                  VS                  E0               RHO_0
                .135                .081                 1.1                   0                   0
#              ALPHA                BETA
                   5                   5
/FAIL/JOHNSON/3
#                 D1                  D2                  D3                  D4                  D5
                .112                .123                -1.5                .007                   0
#              EPS_0  Ifail_sh  Ifail_so                                    Dadv               Ixfem
                1E-6         0         1                                       0                   0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

Comments

In this model, the material behaves as a linear-elastic material when the equivalent stress is lower than the plastic yield stress. For higher stress values, the material behavior is plastic and the stress is calculated as:
$σ = (a + b {ε_{p}}^{n}) (1 + c \ln \frac{\dot{ε}}{{\dot{ε}}_{0}}) (1 - {(T^{*})}^{m})$ $σ = (a + b {ε_{p}}^{n}) (1 + c \ln \frac{\dot{ε}}{{\dot{ε}}_{0}}) (1 - {(T^{*})}^{m})$
Where,
$T^{*} = \frac{T - T_{r}}{T_{m e l t} - T_{r}}$ $T^{*} = \frac{T - T_{r}}{T_{m e l t} - T_{r}}$
Where,

$ε_{p}$ $ε_{p}$

Plastic strain

$\dot{ε}$ $\dot{ε}$

Strain rate

$T$ $T$

Temperature

T_r

Reference temperature

T_melt

Melting temperature

When /HEAT/MAT (with I_form = 1) references this material model, the values of T_r and T_melt defined in this card will be overwritten by the corresponding T₀ and T_melt defined in /HEAT/MAT.
When the temperature is not initialized using /HEAT/MAT or /INITEMP, the reference temperature (T_r) is also the initial temperature.

Figure 1.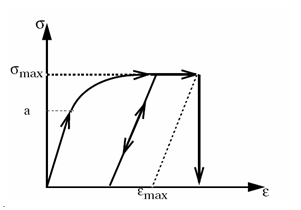
The plastic yield stress should always be greater than zero. To model pure elastic behavior, the plastic yield stress will be set to 10³⁰.
When $ε_{p}$ $ε_{p}$ reaches the value of $ε_{p}^{m a x}$ $ε_{p}^{m a x}$ (for tension, compression or shear), in one integration point, the deviatoric stress of the corresponding integration point is permanently set to 0, however, the solid element is not deleted.
The plastic hardening exponent, n, must be less than or equal to 1.
To eliminate the effect of the strain rate, either set the value of c equal to 0 or set the reference strain rate ( ${\dot{ε}}_{0}$ ${\dot{ε}}_{0}$ ) equal to 10³⁰. There is no effect of strain rate when $\dot{ε}$ $\dot{ε}$ is less than ${\dot{ε}}_{0}$ ${\dot{ε}}_{0}$ .
By default, the hydrostatic pressure is linearly proportional to volumetric strain:
$P = K μ$ $P = K μ$
Where, $K = \frac{E}{3 (1 - 2 ν)}$ $K = \frac{E}{3 (1 - 2 ν)}$ is the bulk modulus and $μ = \frac{ρ}{ρ_{0}} - 1$ $μ = \frac{ρ}{ρ_{0}} - 1$ is the volumetric strain.
An additional Equation of State (/EOS) card can refer to this material in order to incorporate a nonlinear dependency between hydrostatic pressure and volumetric strain.