RD-E: 2000 Ice Cube
Ice cube dropping on two sliding channels.
Figure 1.
The subject in this example demonstrates the falling and sliding of an ice cube on to sloped beams using an explicit transient dynamic analysis for deformable, free-flying objects. The impact and rebound are modeled using penalty contact algorithms.
The Contact between the ice cube, the beams, and the cup are modeled using different penalty contact interfaces (/INTER/TYPE7, /INTER/TYPE24 and /INTER/TYPE25). The ice cube and the beams are modeled using hexahedron elements. The cup is modeled with standard shell elements.
Options and Keywords Used
- Boundary conditions on node groups for translational and rotational motion
(/BCS):
- The ice cube nodes are constrained in the Y translation.
- The bottom nodes of the beams are constrained in all directions.
- The cup is constrained in all directions
- Gravity (/GRAV):
- A gravity load (g = 9.81 m/s2) in the Z-direction is applied on the ice cube’s nodes
- Interfaces: Three different node to surface penalty contact interfaces are
compared with each other. For each model, the ice cube is the secondary and
the main is the beams and cup.
- /INTER/TYPE7 interface uses the penalty method with an initial gap of 0.1. Ice cube nodes are the secondary and the main surface is defined using the upper surface of the beams and the cup. To replicate surface to surface contact, a second TYPE7 contact is created with the ice cube as main surface and the beams and cup as secondary nodes. The interface stiffness is the minimum value of the main and secondary stiffness (Istf = 4). The TYPE7 interface is a general impact interface with a nonlinear stiffness. In case of high impact speed or contacts with a small gap, the time step can be reduced because the contact stiffness will increase if the secondary node penetrates closer to the main surface.
- /INTER/TYPE24 interface uses the penalty method without any contact gap between the solid elements. A surface to surface contact is defined where the ice cube is defined as a secondary surface and the main surface is defined using the upper surface of the beams and the cup. The interface stiffness is the minimum value of the main and secondary stiffness (Istf = 4). The TYPE24 interface is a general nodes-to-surface contact interface using the penalty method with a constant interface stiffness which means there is no reduction in time step due to secondary node penetration. Three different input types can be used: single surface, surface to surface, or nodes to surface. This contact is typically used for drop test simulations.
- /INTER/TYPE25 is very similar to TYPE24 in its definition and algorithm. However, it is being developed for crash impact simulations and; therefore, has a few different options and algorithms.
- /PROP/TYPE1 (SHELL)
- /PROP/TYPE14 (SOLID)
Input Files
Model Description
This problem provides a comparison of different contact interfaces that allow sliding contact between an ice cube and steel beams.
The cube is submitted to gravity and slides on declined fixed beams. Finally, it is collected in a cup. The width of the cube is 30 mm and the dimensions of the beams are 40 x 30 x 500 mm.
- Material Properties
- Value
- Initial density
- 9.16e-10
- Young's modulus
- 8996
- Poisson's ratio
- 0.3
- Yield Stress, SIGY
- 1.0
- Hardening parameter, b
- 4.0
- Hardening exponent, n
- 0.5
- Material Properties
- Value
- Initial density
- 7.8e-09
- Young's modulus
- 210000
- Poisson's ratio
- 0.3
- Yield stress, SIGY
- 200
- Hardening parameter, b
- 400
- Hardening exponent, n
- 0.5
Units: mm, s, Mg, N, MPa
Results
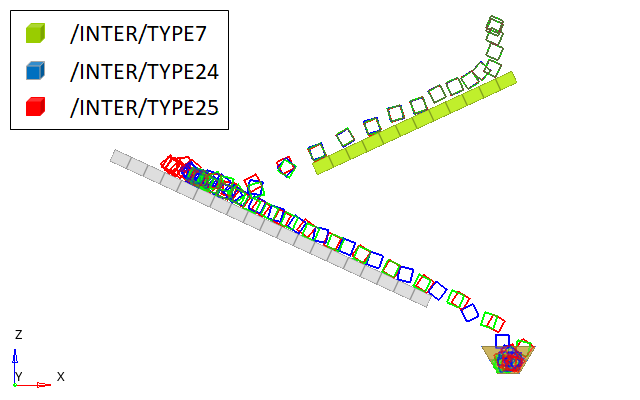
Figure 2. Trajectory of the Ice Cube using Interface TYPE7, TYPE24 and TYPE25
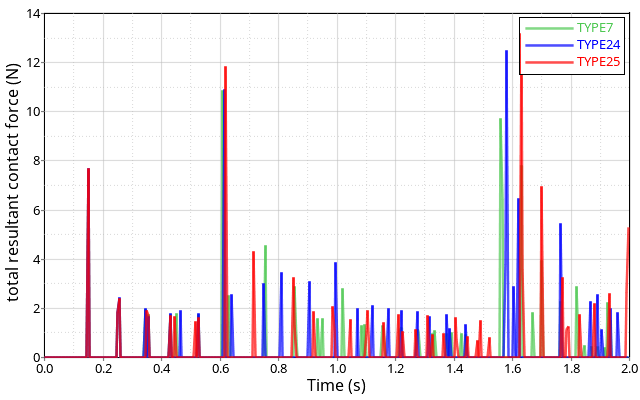
Figure 3. Comparison of the Reaction Forces of the Ice Cube on the Beams