RD-E: 0700 Pendulums
The purpose of this example is to study the energy propagation and the momentum transfer through several bodies, initially in contact with each other, subjected to multiple impact. The process of collision and the energetic behavior upon impact are described using a 3-dimensional mode.
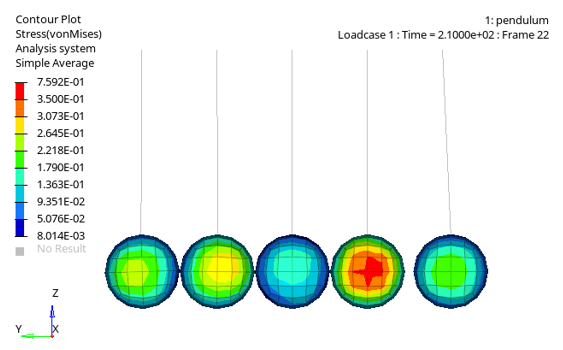
Figure 1.
This example simulates the oscillation and wave propagation of a group of pendulums in a line when impacted at one end. The material is elastic. The quality of the model first depends on how the contact is managed. For this model a TYPE24 contact interface using penalty method is used.
Options and Keywords Used
- 3-dimensional analysis, truss (thread), brick and brick (hexahedron elements)
- /INTER/TYPE2
- /INTER/TYPE14
- General nodes-to-surface contact interface using the penalty method (/INTER/TYPE24)
- Elasticity, momentum transmission, shock wave propagation, multiple impacts.
- Gravity (/GRAV)
- Boundary conditions on node groups for translational and rotational motion (/BCS)
Input Files
Model Description
Five pendulums in line, initially in contact with each other, are struck by a sixth one. The shock wave and oscillating motion are observed.
Units: g, ms, mm, MPa
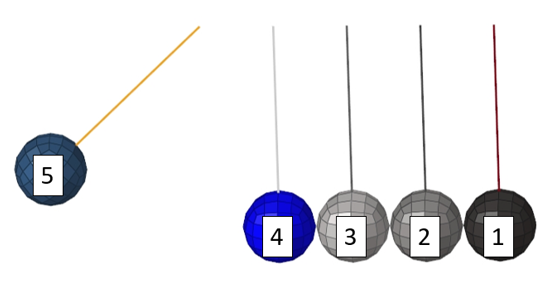
Figure 2. 3-dimensional Mesh in Initial State
- Properties
- Value
- Young's modulus
- 70000
- Poisson's ratio
- 0.33
- Density
- 0.0027
- Truss
- Length
- 124.6 mm
- Ball
- Radius
- 25.4 mm
- Mass
- 169.7 g
A TYPE24 contact interface uses a penalty method with a linear contact stiffness to model the contact between the balls. A self-contact definition between all the balls is used to model the contact between the nodes and the element surface. Interfaces using the penalty method are based on main/secondary treatment.
Brick elements are used to model the balls. No contact gap is required for the TYPE24 interface.
Gravity is applied to all nodes. A gravity versus time function is applied to define the gravity acceleration in the Z direction. Gravity is activated by the /GRAV option.
The top of the trusses are fixed in X, Y and Z translations and in Y and Z rotations (free in X rotation).
Results
When considering the kinetic energy variation of the model, the system behaves as a simple pendulum (Figure 3).
- Vertical displacement of the ball’s center
- Velocity
- Mass
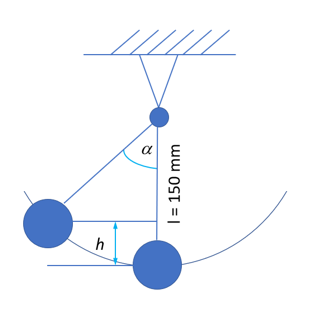
Figure 3. Pendulum Motion
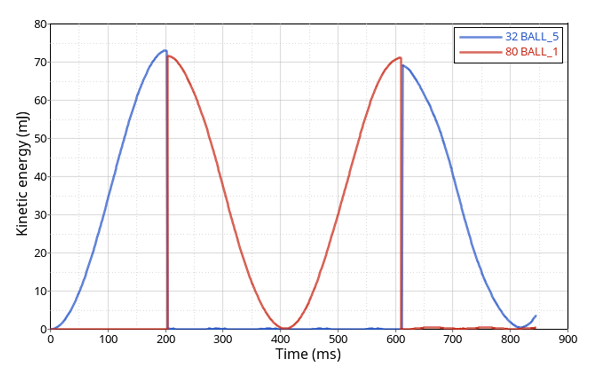
Figure 4. Kinetic Energy Transfer between Ball 5 and Ball 1
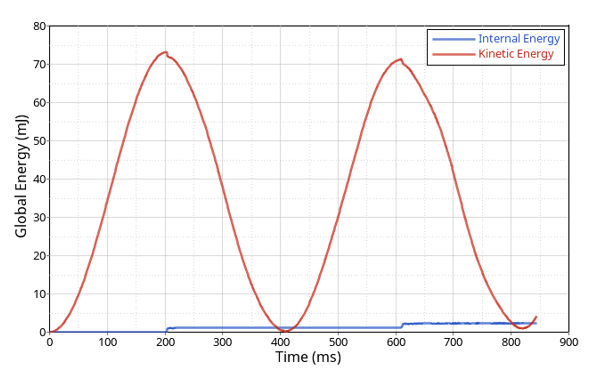
Figure 5. Global Internal and Kinetic Energy
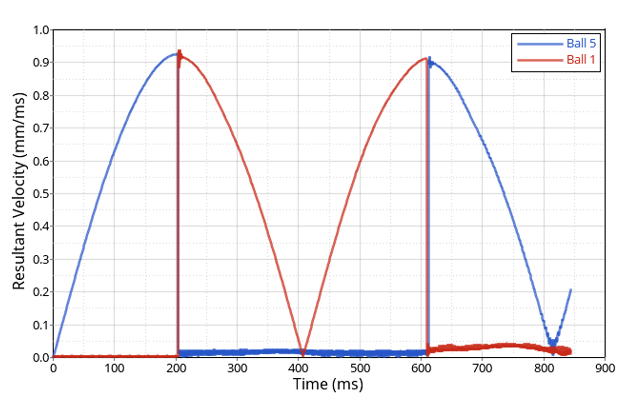
Figure 6. Velocity Curve of Ball 5 and Ball 1
Conclusion
The oscillation and wave propagation of a group of pendulums, arranged in a line was studied using Radioss. The model has a coarse mesh with 3D elements to reduce the computation time. The contact was modeled with /INTER/TYPE24 using penalty method. Results were compared to an analytical solution where the pendulum system is assimilated to a simple pendulum. The results obtained by simulation and theory demonstrate the validity of the numerical results obtained by Radioss.