RD-E: 0602 Fluid Flow
Fuel tank overturning with simulation of the fluid flow. The reversing tank is modeled using horizontally-applied gravity. The tank container is presumed without deformation and only the water and air inside the tank are taken into consideration using the ALE property formulation, Iale=1.
The fluid flow is studied during the fuel tank overturning. This example uses the ALE (Arbitrary Lagrangian Eulerian) formulation and the hydrodynamic bi-material law (/MAT/LAW37) to simulate interaction between water and air. The tank container is presumed to be without deformation and it will not be modeled.
Options and Keywords Used
- Fluid flow simulation and ALE formulation
- Brick elements
- Hydrodynamic and bi-phase liquid gas (/MAT/LAW37 (BIPHAS))
- ALE boundary conditions (/ALE/BCS)
- Gravity (/GRAV)
- ALE property formulation with Iale=1
- Material velocity
- Grid velocity
All nodes inside the border have grid and material velocities fixed in the Z direction; the nodes on the left and right sides have a material velocity fixed in the X and Z directions, while the nodes on the high and low sides have a material velocity fixed in the Y and Z directions. The grid velocity is fully fixed on the border, just as the material velocity is fixed on the corners.
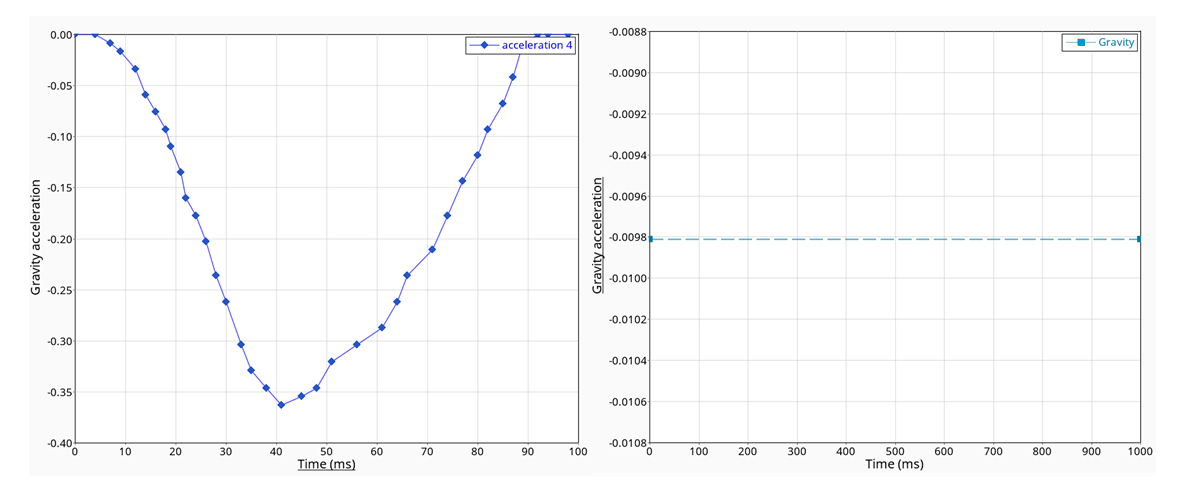
Figure 1. Left: Variable Acceleration; Right: Gravity
Input Files
Model Description
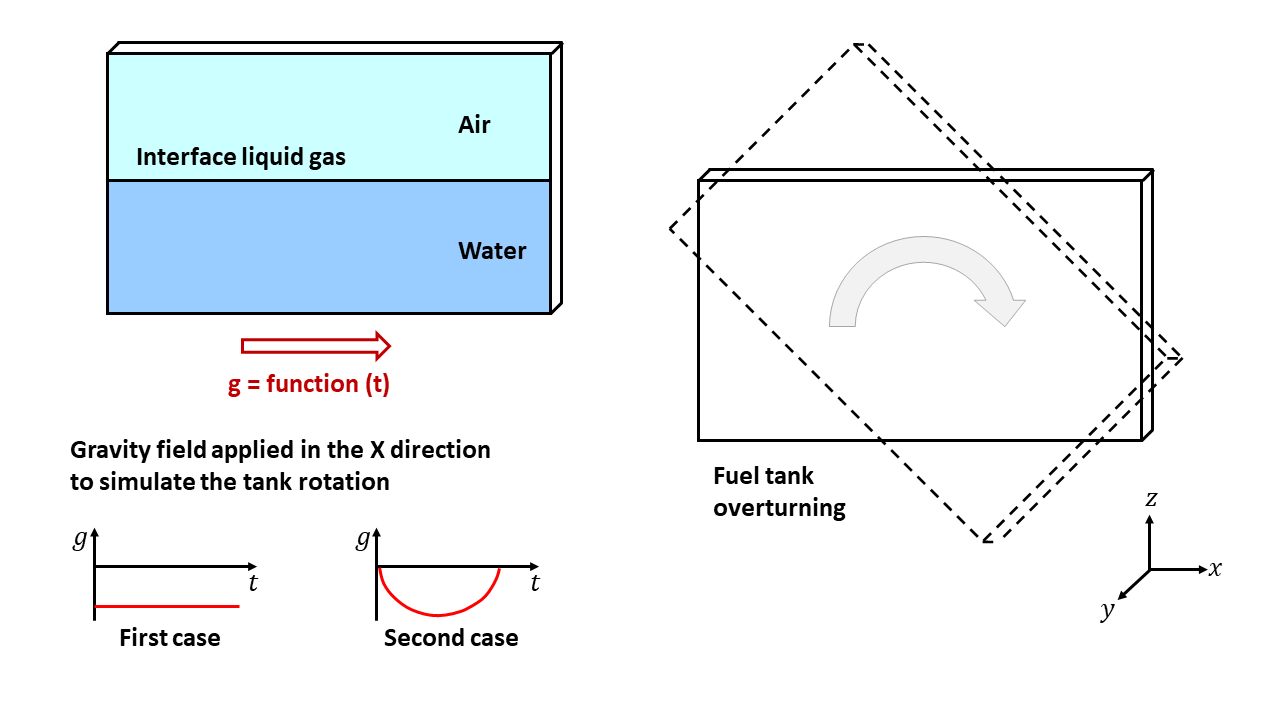
Figure 2. Problem Description
The example deals with two loading cases: an instantaneous rotation of the fuel tank by 90 degrees (gravity function 1) and a progressive rotation (gravity function 2).
- Material Properties
- Values
- Air density
- 1.22x10-6
- Water density
- 0.001
- Gas initial pressure
- 0.1
Model Method
The bi-material air-water is described in the hydrodynamic material law (/MAT/LAW37). See previous section for information about this law, including full input data.
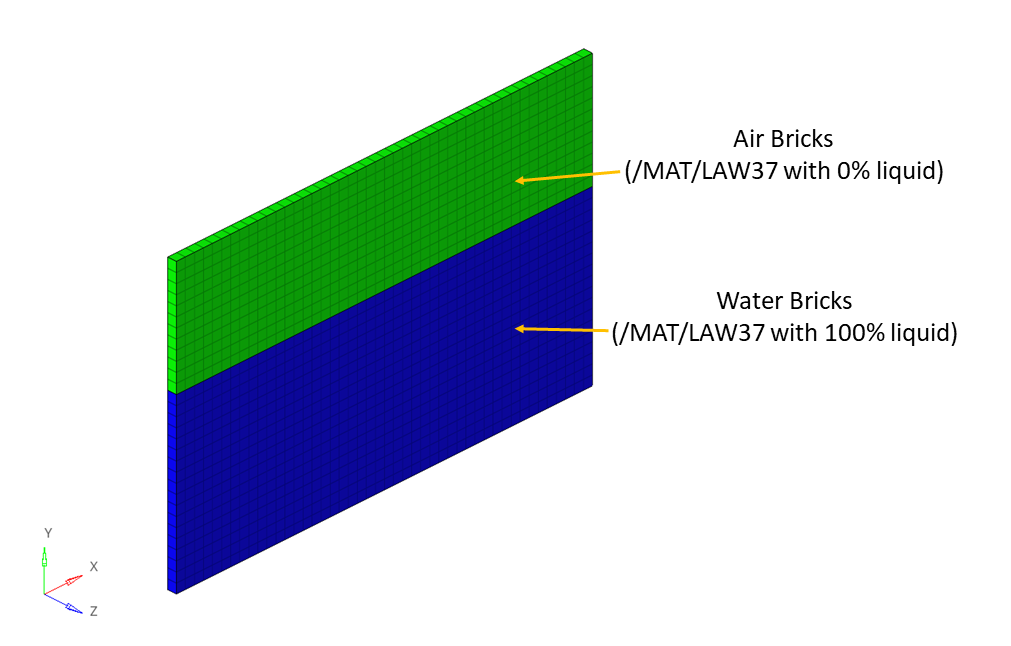
Figure 3. Air and Water Mesh (ALE bricks)
Using the ALE formulation, brick mesh is only deformed by the tank deformation, the water flowing through the mesh. The Lagrangian shell nodes still coincide with the material points, while the elements are deformed with the material: this is the Lagrangian mesh. For the ALE mesh, nodes on boundaries are fixed to remain on the border, while the interior nodes are moved.
Results
Curves and Animations
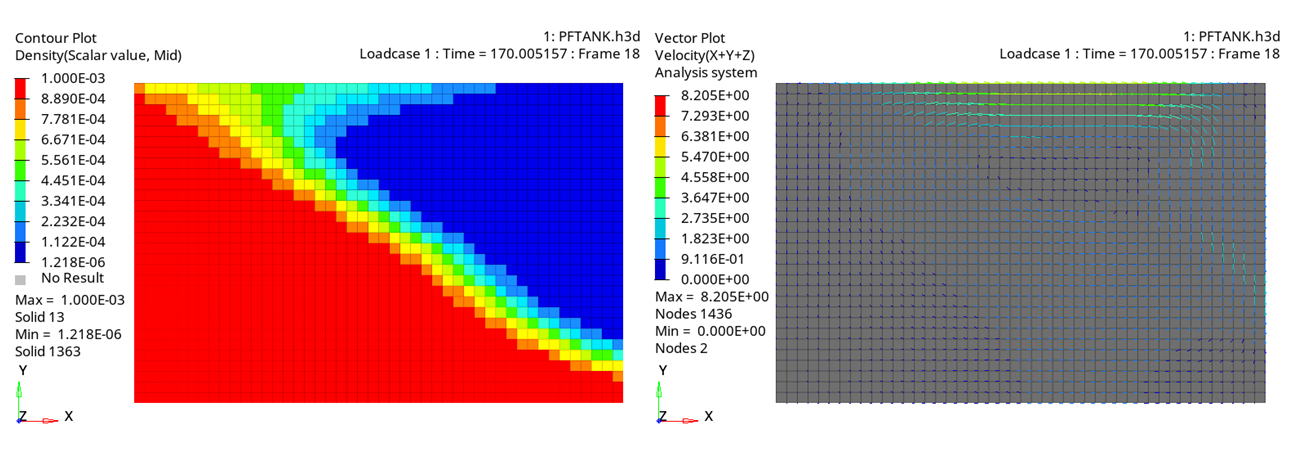 Figure 4. Model with Constant Acceleration (Gravity function 1) - Time = 170 ms
Figure 4. Model with Constant Acceleration (Gravity function 1) - Time = 170 ms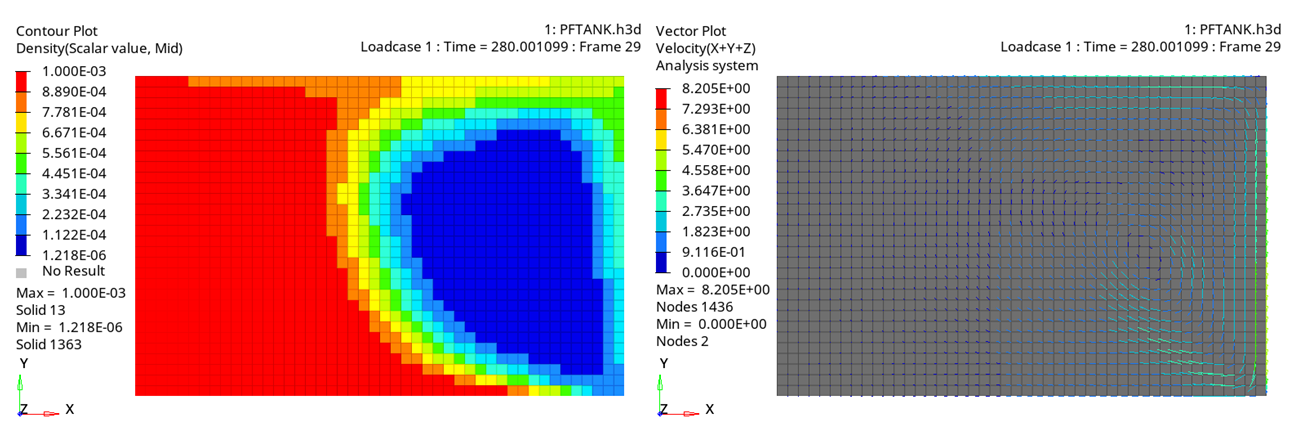 Figure 5. Model with Constant Acceleration (Gravity function 1) - Time = 280 ms
Figure 5. Model with Constant Acceleration (Gravity function 1) - Time = 280 ms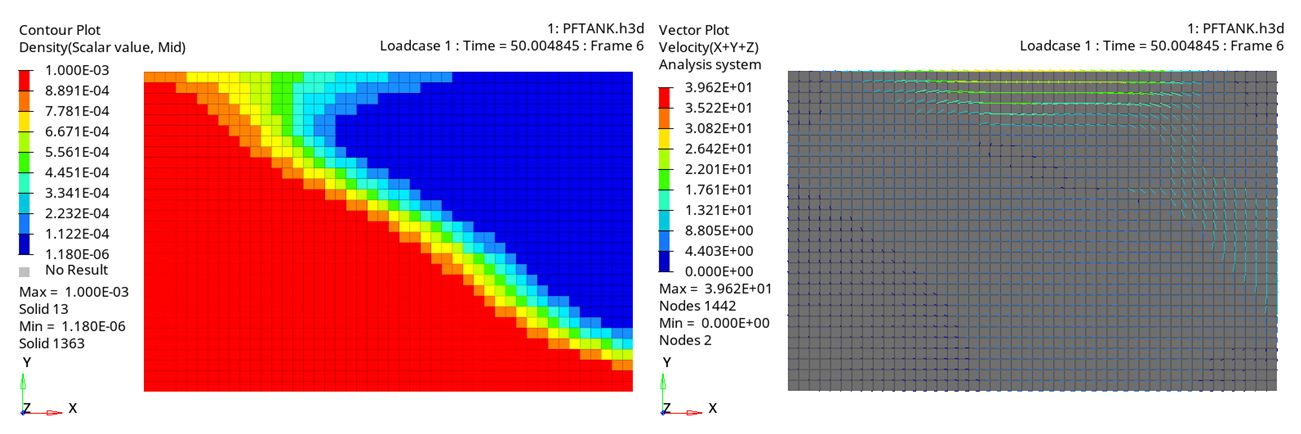 Figure 6. Model with Variable Acceleration(Gravity function 2) - Time = 50 ms
Figure 6. Model with Variable Acceleration(Gravity function 2) - Time = 50 ms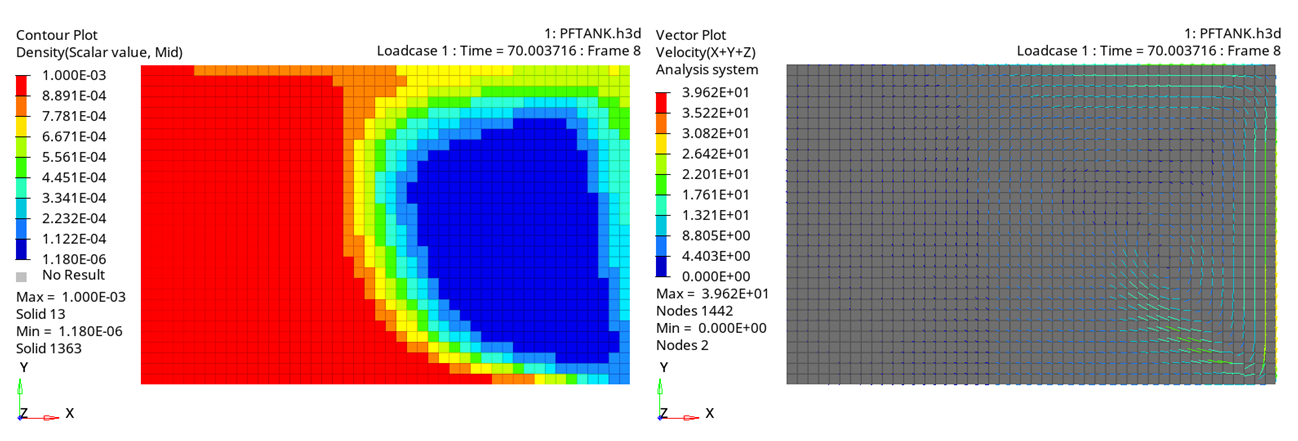 Figure 7. Model with Variable Acceleration (Gravity function 2) - Time = 70 ms
Figure 7. Model with Variable Acceleration (Gravity function 2) - Time = 70 msConclusion
This example studied hydrodynamic bi-material using LAW37 in Radioss, using ALE formulation is used. The application of boundary conditions in ALE formations and handling the fluid-structure interaction were discussed. Furthermore, the results obtained correctly represent the physical problem.