RD-E: 4300 Perfect Gas Modeling with Polynomial EOS
The purpose of this example is to plot numerical pressure, internal energy, and sound speed for a perfect gas material law.
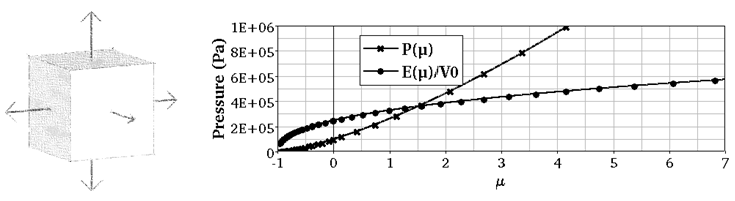
Figure 1.
A simple test of compression/expansion is made to compare these formulation outputs with theoretical results.
Options and Keywords Used
- Perfect gas
- Polynomial EOS (/EOS/POLYNOMIAL)
- Absolute / Relative formulations
- Pressure shift
- Hydrodynamic fluid material (/MAT/LAW6 (HYDRO or HYD_VISC))
- Imposed displacement (/IMPDISP)
- Lagrangian boundary conditions (/ALE/BCS)
- Nodes on each of the faces are moved with imposed displacement (/IMPDISP)
- Element pressure, density and internal energy density are saved in the Time Histories file
Input Files
Model Description
Figure 2.
The fluid will be assumed to be a perfect gas. Volume is changed in the three directions to consider a pure compression followed by an expansion of matter (Figure 3).
This test will be modeled with a single ALE element (8 node brick) and polynomial EOS.
Evolutions of pressure, internal energy and sound speed will be compared between numerical output and theoretical results.
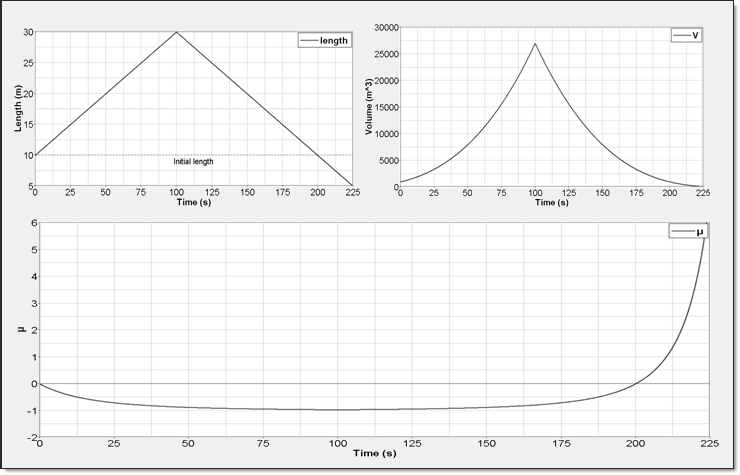
Figure 3. Elementary volume change
Simulation Iterations
A single ALE brick element is used. Material is confined inside the element by defining brick nodes as Lagrangian. For each face, displacement is imposed on the four nodes along the normal.
Polynomial EOS
- Incompressible gas
- Linear elastic material
- Perfect gas
This example is focused only on Perfect Gas modeling.
Results
Theoretical Results
- Pressure:Perfect gas pressure is given by:
(5) Then,(6) Radioss assumes the hypothesis of an isentropic process to compute the change in internal energy:(7) This theory gives the following differential equation:(8) This has the form and the general solution is:(9) Pressure is also polytropic:(10) (11) Here, is the material constant (ratio of heat capacity). For diatomic gas =1.4. Air is made mainly of diatomic gas, so set gamma to 1.4 for air.
- Internal Energy:
- Sound Speed:Perfect gas sound speed is:
(13) Equation 11 gives its expression in term of volume:(14)
| Pressure (Pa) | Internal Energy Density (J) | Sound Speed (m/s) | |||
|---|---|---|---|---|---|
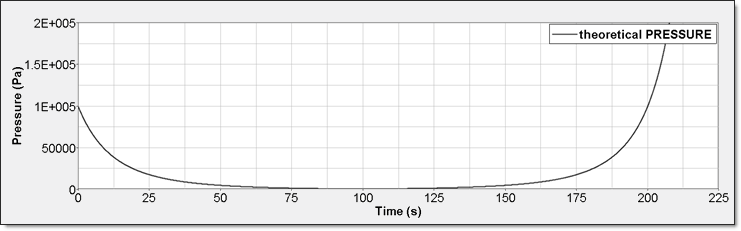
Figure 4. Perfect Gas Pressure
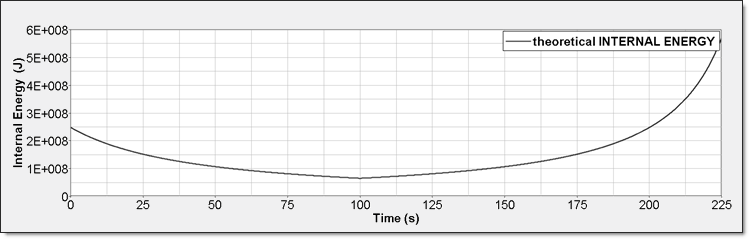
Figure 5. Perfect Gas Internal Energy
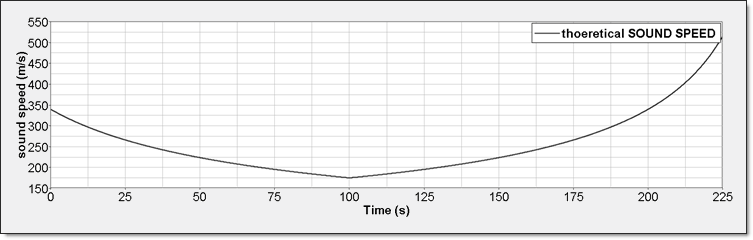
Figure 6. Perfect Gas Sound Speed
Material Control Cards
| Case | Mathematical Model | Pressure | Energy |
|---|---|---|---|
| 1 | absolute | absolute | |
| 2 | relative | absolute | |
| 3 | relative | relative | |
| 4 | absolute | relative |
Sound Speed and Time Step
| Case | C0 | C1 | C4 | C5 | c2
From Equation 25 |
Comparison with Theoretical Value |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | ||||
| 2 | 0 | 0 | ||||
| 3 | ||||||
| 4 |
For each of the four formulations, the computed sound speed by Radioss is the same as the theoretical one. Time step and cycle number are also not affected.
Case 1: Both Pressure and Energy are Absolute Values
- Pressure:Equation of State:
(30) Where,
Identifying the polynomial coefficients leads to:(31) Where,
- Corresponding
Input:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----| /MAT/HYD_VISC/1 Polynomial EOS-Absolute Pressure-Absolute Energy # RHO_I RHO_0 1.204 0 # Knu Pmin 0 0 /EOS/POLYNOMIAL/1 Polynomial EOS-Absolute Pressure-Absolute Energy # C0 C1 C2 C3 0 0 0 0 # C4 C5 E0 Psh RHO_0 .4 .4 250000 0 1.204 #---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----| - Output Results:
Table 4. Time History Measure Initial Value Unit /TH/BRICK () Pressure /TH (IE) Energy /TH/BRICK (IE) Pressure - Comparison with Theoretical Result:Numerical result for perfect gas pressure is given by time history. Element time history (/TH/BRICK) allows displaying it. This result is compared to a theoretical one. Curves are superimposed.
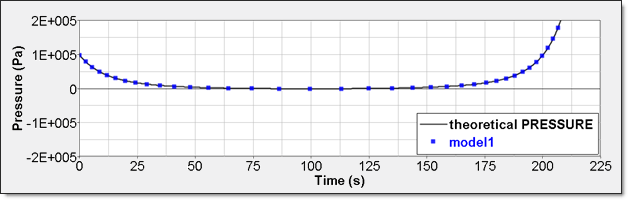
Figure 7. Numerical Pressure, Model 1Internal energy can be obtained through two different ways. The first one is internal energy density () recorded by element time history (/TH/BRICK). The second one is the internal energy from the global time history because the model is composed of a single element.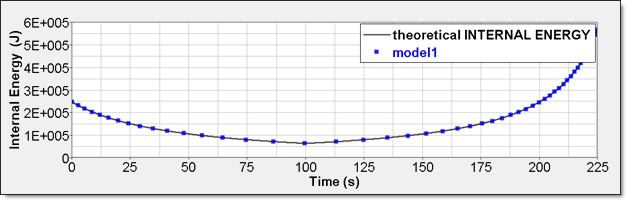
Figure 8. Numerical Internal Energy, Model 1
Case 2: Pressure is Relative and Energy is Absolute
- Pressure:Equation of State:
(32) Relative Pressure:(33) Identifying with polynomial coefficients leads to:(34) Where,
Minimum Pressure:(35) Due to , the minimum pressure must be set to a non-zero value.
- Corresponding
Input:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----| /MAT/HYD_VISC/1 Polynomial EOS-Relative Pressure-Absolute Energy # RHO_I RHO_0 1.204 0 # Knu Pmin 1.5256E-5 -100000 /EOS/POLYNOMIAL/1 Polynomial EOS-Relative Pressure-Absolute Energy # C0 C1 C2 C3 0 0 0 0 # C4 C5 E0 Psh RHO_0 .4 .4 250000 100000 1.204 #---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----| - Output Result:
Time History Measure Initial Value Unit /TH/BRICK () 0 Pressure /TH (IE) Energy /TH/BRICK (IE) Pressure - Comparison with Theoretical Result:
Numerical result for perfect gas pressure is given by time history. Element time history (/TH/BRICK) allows displaying it. This result is compared to a theoretical one. Curves are superimposed.
Element time history (/TH/BRICK) is the pressure relative to Psh. The resulting curve is then shifted with Psh value and starts from 0.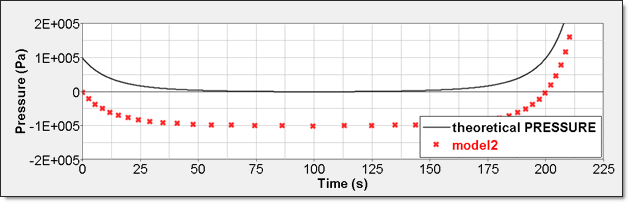
Figure 9. Numerical Pressure, Model 2Internal energy can be obtained through two different ways. The first one is internal energy density () recorded by element time history (/TH/BRICK). The second one is the internal energy from the global time history because the model is composed of a single element.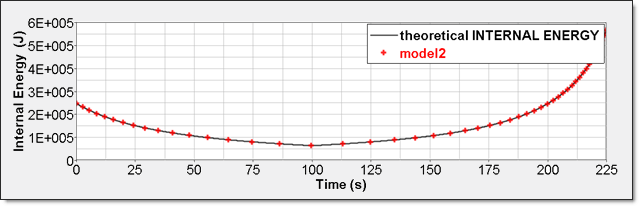
Figure 10. Numerical Internal Energy, Model 2
Case 3: Both Pressure and Energy are Relative
- Pressure:Equation of State:
(36) Initial internal energy can be introduced:(37) Pressure from a reference one provides:(38) Where, .
Identifying with polynomial coefficients leads to:(39) Where, , , and .
Minimum Pressure:(40) Due to , the minimum pressure must be set to a non-zero value.
- Corresponding
Input:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----| /MAT/HYD_VISC/1 Polynomial EOS-Relative Pressure-Absolute Energy # RHO_I RHO_0 1.204 0 # Knu Pmin 1.5256E-5 -100000 /EOS/POLYNOMIAL/1 Polynomial EOS-Relative Pressure-Absolute Energy # C0 C1 C2 C3 100000 100000 0 0 # C4 C5 E0 Psh RHO_0 .4 .4 0 100000 1.204 #---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----| - Output Results:
Time History Measure Initial Value Unit /TH/BRICK () 0 Pressure /TH (IE) 0 Energy /TH/BRICK (IE) 0 Pressure - Comparison with Theoretical Result:
Numerical result for perfect gas pressure is given by time history. Element time history (/TH/BRICK) allows displaying it. This result is compared to a theoretical one. Curves are superimposed.
Element time history (/TH/BRICK) is the pressure relative to Psh. The resulting curve is then shifted with Psh value and starts also from 0.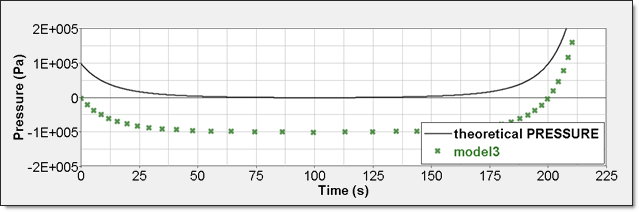
Figure 11. Numerical Pressure, Model 3Internal energy can be obtained through two different ways. The first one is internal energy density () recorded by element time history (/TH/BRICK). The second one is the internal energy from the global time history because the model is composed of a single element. This numerical internal energy is relative to its initial value; it is shifted with the value from the absolute theoretical one and also starts from 0.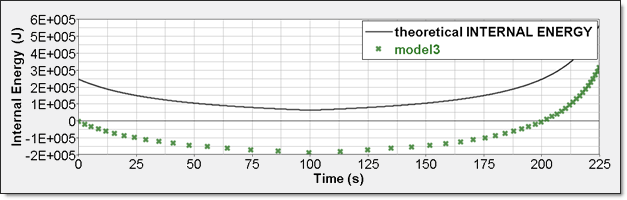
Figure 12. Numerical Internal Energy, Model 3
Case 4: Pressure is Absolute and Energy is Relative
- Pressure:Equation of State:
(41) Initial internal energy can be introduced:(42) Pressure from a reference provided:(43) Identifying with polynomial coefficients leads to:(44) Where, ;
- Corresponding
Input:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----| /MAT/HYD_VISC/1 Polynomial EOS-Relative Pressure-Absolute Energy # RHO_I RHO_0 1.204 0 # Knu Pmin 1.5256E-5 0 /EOS/POLYNOMIAL/1 Polynomial EOS-Relative Pressure-Absolute Energy # C0 C1 C2 C3 100000 100000 0 0 # C4 C5 E0 Psh RHO_0 .4 .4 0 0 1.204 #---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----| - Output Results:
Time History Measure Initial Value Unit /TH/BRICK () Pressure /TH (IE) 0 Energy /TH/BRICK (IE) 0 Pressure - Comparison with Theoretical Result:Element time history (/TH/BRICK) gives absolute pressure. This result is compared to a theoretical one. Curves are superimposed.
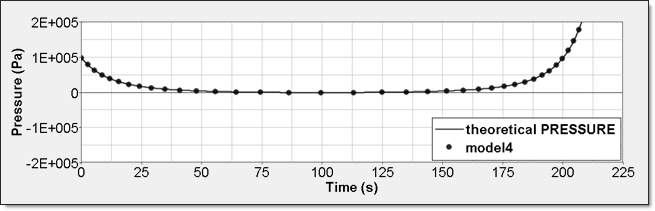
Figure 13. Numerical Pressure, Model 4Internal energy can be obtained through two different ways. The first one is internal energy density () recorded by element time history (/TH/BRICK). The second one is the internal energy from the global time history because the model is composed of a single element. This numerical internal energy is relative to its initial value; it is shifted with the value from the absolute theoretical one and also starts from 0.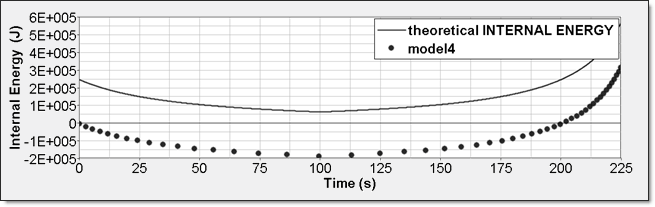
Figure 14. Numerical Internal Energy, Model 4