RD-E: 1000 Bending
Pure bending test with different 3- and 4-nodes shell formulations.

Figure 1.
Options and Keywords Used
At one extremity of the beam, all DOF are blocked. A rotational velocity is imposed on the main node of the rigid body placed on the other side.
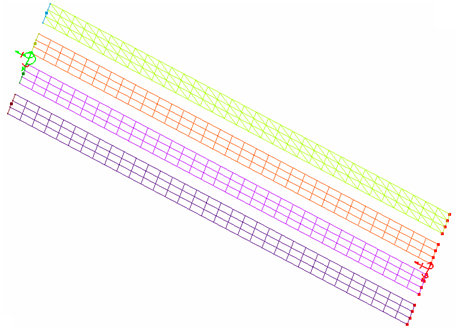
Figure 2. Beam Meshes
Input Files
Model Description
The purpose of this example is to study a pure bending problem. A cantilever beam with an end moment is studied. The moment variation is modeled by introducing a constant imposed velocity on the free end.
The following system is used: mm, ms, g, N, MPa
Several kinds of element formulation are used.
- Material Properties
- Value
- Initial density
- 0.01
- Reference density
- .01
- Young's modulus
- 1000
- Poisson ratio
- 0
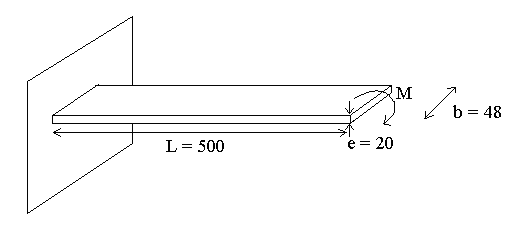
Figure 3. Geometry of the Problem
Model Method
- Q4 mesh with the Belytshcko & Tsay formulation (Ishell =1, hourglass control TYPE1, TYPE2, and TYPE3)
- Q4 mesh with the QEPH formulation (Ishell =24)
- Q4 mesh with the QBAT formulation (Ishell =12)
- T3 mesh with the DKT18 formulation (Ishell =12)
Results
Numerical Results and Analytical Solution Comparison
As shown in Figure 3, rotation around X and displacement with regard to Y of the free end are studied.
The following tables summarize the results obtained for the different formulations. From an analytical point of view, the beam deformed under pure bending must satisfy the conditions of the constant curvature which implies that for = , the beam should form a closed ring. However, depending on the finite element used, a small error can be observed, as shown in the following tables. This is mainly due to beam vibration during deformation as it is highly flexible. Good results are obtained by the QBAT, QEPH and DKT18 elements, respectively. This is mainly due to the good estimation of the curvature in the formulation of these elements. The BT family of under-integrated shell elements is less accurate. With the TYE3 hourglass formulation, the model remains stable until = 6rad. However, the moment-rotation curves do not correspond to the expected response.
To reduce the overall computation error, smaller explicit time steps are used by reducing the scale factor in /DT. The results reported in the end table show that a reduction in the time step enables to reduce the error accumulation, even though the divergence problems for BT elements cannot be avoided.
| BATOZ | QEPH | BT | DKT | |
|---|---|---|---|---|
| Scale factor | 0.6 | 0.9 | 0.9 | 0.2 |
| Imposed velocity rot. | 0.005 rad/ms | 0.005 rad/ms | 0.005 rad/ms | 0.005 rad/ms |
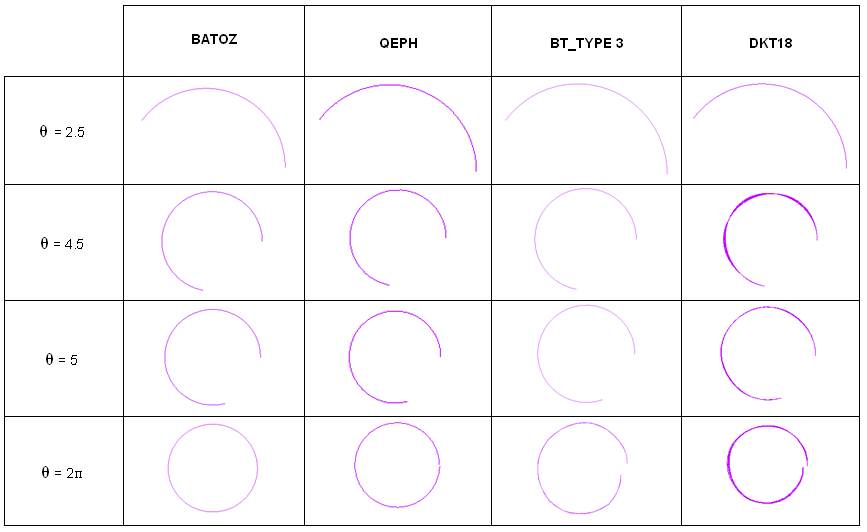
Figure 4.

Figure 5. Moment versus Rotation Around X
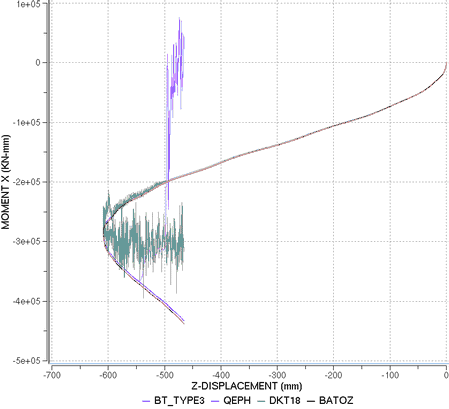
Figure 6. Moment versus Displacement Along Z
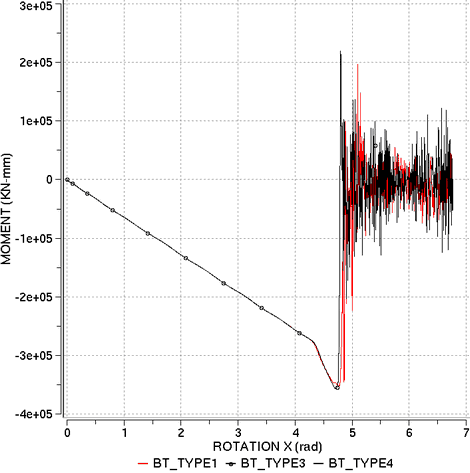
Figure 7. Moment versus Rotation Around X
| BATOZ | QEPH | BT | DKT | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sf=0.9 | Sf =0.8 | Sf =0.6 | Sf =0.9 | Sf =0.8 | TYPE1 | TYPE3 | TYPE4 | Sf =0.3 | Sf =0.2 | Sf =0.1 | ||||
| Sf =0.9 | Sf =0.1 | Sf =0.9 | Sf =0.1 | Sf =0.9 | Sf =0.1 | |||||||||
| CPU (normalized) # cycles |
2.18 97600 |
2.43 109800 |
3.14 146400 |
1.23 95800 |
1.34 107800 |
42.64 59100 |
7.07 552600 |
2.62 182300 |
108.60 -- |
1.03 59100 |
7.17 552600 |
5.44 364100 |
8.21 621600 |
16.21 1243200 |
| Error = 2 (%) |
0% | 0% | 0% | 0% | 0% | 55.3% | 99% | 0% | 0% | 55.9% | 99.9% | 3.4% | 28.88% | 3.7% |
| err
=20% (rad) degree |
6.91 396° |
6.89 395° |
-- | -- | -- | 4.36 250° |
4.53 260° |
6.06 347° |
5.98 343° |
4.38 251° |
4.51 258° |
6.37 365° |
-- | -- |
| Dz
= 2 (mm) |
-500.5 | -500.5 | -500.5 | -500.5 | -500.5 | -491.2 | -525.8 | -518.333 | -506.0 | -529.8 | -433.8 | -476.5 | -496.5 | -499.4 |
| Mx
= 2 (x10+5kN-mm) |
-4.04 | -4.05 | -4.06 | -4.01 | -4.01 | -0.21 | -0.11 | -3.13 | -2.38 | -0.07 | -0.02 | -3.09 | -3.02 |
-3.08 |
Conclusion
- QBAT element
- This formulation gives a -revolution of the beam with no energy error. However, a 20% error is attained for = 384 degrees.
- QEPH element
- This formulation seems to be the best one to treat the problem. It enables a -revolution of the beam to be obtained. The error remains null until = 400 degrees.
- BT formulation
- This formulation does not provide satisfactory results and is not adapted to this simulation, whatever the anti-hourglass formulation. This is mainly due to using a flat plate formulation and the fact that the element is under-integrated. The TYPE3 hourglass formulation seems to be better than others.
- DKT formulation
- The bending is simulated correctly. However, the element is costly and the CPU time is much longer.