CG Card
The CG card defines the method to solve the matrix equation.
On the Solve/Run tab, in the Solution
settings group, click the ![]() Preconditioner icon.
Preconditioner icon.
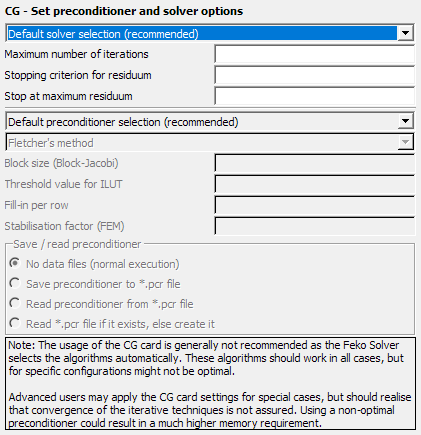
Normally the CG card should not be used. Feko automatically selects optimal solution techniques, preconditioners and other options depending on the problem type. These algorithms should be sufficient in all cases, but they might not be optimal for specific MLFMM and FEM configurations that use iterative solvers.
For these specific solutions, advanced users could apply the CG card after consultation
with Feko technical support. Nevertheless convergence of the
iterative techniques cannot be guaranteed. In addition the memory requirements could be
higher than what is desired.
Warning: Any models derived from models containing a
CG card should also be re-considered if they contain a CG card.
Parameters:
Matrix solution method:
- Default solver selection (recommended). When this option is selected, then Feko will automatically select a suitable solver along with all its required parameters. The choice depends on whether Feko is executed sequentially or in parallel, but also which solution method is employed (for example direct LU decomposition solver for the MoM while an iterative solver is used for MLFMM or FEM). This option has, regarding the solver type, the same effect as not using a CG card, but still allows the user to change the default termination criteria for the iterative solver types, or to change the preconditioner.
- Gauss elimination (LINPACK routines) Use Gauss elimination from the LINPACK routines.
- Conjugate Gradient Method (CGM)
- Biconjugate gradient method (BCG)
- Iterative solution with band matrix decomposition
- Gauss elimination (LAPACK routines) Use Gauss elimination from the LAPACK routines.
- Block Gauss algorithm (matrix saved to disk) The block Gauss algorithm is used (in case the matrix has to be saved on the hard disk, for example when a sequential out-of-core solution is performed).
- CGM (Parallel Iterative Method)
- BCG (Parallel Iterative Method)
- CGS (Parallel Iterative Method)
- Bi-CGSTAB (Parallel Iterative Method)
- RBi-CGSTAB (Parallel Iterative Method)
- RGMRES (Parallel Iterative Method)
- RGMRESEV (Parallel Iterative Method)
- RCGR (Parallel Iterative Method)
- CGNR (Parallel Iterative Method)
- CGNE (Parallel Iterative Method)
- QMR (Parallel Iterative Method)
- TFQMR (Parallel Iterative Method)
- Parallel LU-decomposition (with ScaLAPACK routines). The parallel LU decomposition with ScaLAPACK (solution in main memory) or with out-of-core ScaLAPACK (solution with the matrix stored to hard disk). This is the default option for parallel solutions and normally the user need not change it.
- QMR (QMRPACK routines)
- Direct sparse solver. Direct solution method for the ACA or FEM
(no preconditioning).
When using the parallel , the factorisation type, which slightly impacts runtime and memory, can be specified.
- Maximum number of iterations
- The maximum number of iterations for the iterative techniques.
- Stopping criterion for residuum
- Termination criterion for the normalised residue when using iterative methods. The iterative solver will stop when the normalised residue is smaller than this value.
- Stop at maximum residuum
- For the parallel iterative methods, the solution is terminated when the residuum becomes larger than this value. The iterative solution will stop with an error message indicating that the solution has diverged.
- Preconditioners
- Refer to Preconditioners for MLFMM and Preconditioners for FEM for more information.
- Save/read preconditioner
- For the incomplete LU preconditioners used with the FEM the preconditioner can be computed only once and written to a .pcr file. Then for a subsequent solution it can be read from this file saving runtime. Since the FEM preconditioners depend only on the FEM part of the matrix, this method is useful when only the MoM part of a FEM/MoM problem has changed.