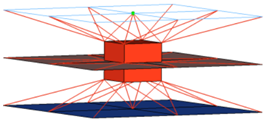
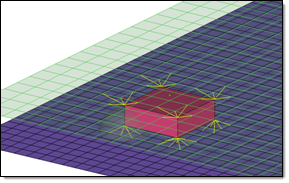
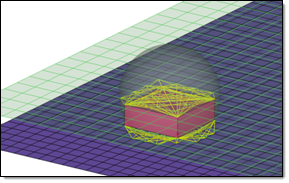
Hexa (Rigid)

Restriction: Available in Abaqus, Nastran, and OptiStruct.

Consolidates several ACM definitions into one general, flexible ACM definition. Besides mid thickness, constant thickness, and maintain gaps, the definition of several coats with different hexa patterns is available.

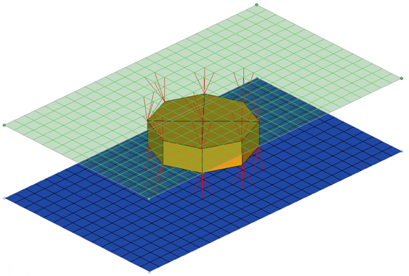
For Nastran and OptiStruct, this realization uses the prop_nastran_acm.tcl property script. For Abaqus, it uses prop_abaqus_acm.tcl.

ACM Realization Options


Option	Action
thickness	Select a thickness option used for dimensioning and positioning hexas. shell gap Project the hexa spot to touch the shell elements. The position is independent from any thickness. equival. (T1+T2)/2 Create hexa elements with RBE3 elements projecting and connecting to the surrounding shell elements. This realization uses the shell thickness to calculate the hexa offset from the shell elements. In the case where the model is a 3T connection, the acm (equivalenced-(T1+T2)/2) realization will join the hexa elements. Figure 2. detached (T1+T2)/2 Create hexa elements with RBE3 elements projecting and connecting to the surrounding shellstr elements. This realization uses the shell thickness to calculate the hexa offset from the shell elements. In the case where the model is a 3T connection, the acm (detached-(T1+T2)/2) realization will not join the hexa elements. Figure 3. mid thickness Calculate the hexa spot size (thickness) as the air gap between the two connected parts. If there is no gap, or even a penetration, the hexa spot size will always be modeled with 1.0. const thickness Specify the hexa spot size (thickness). maintain gaps Calculate the hexa spot size (thickness) as the gap distance reduced by two times the specified value for maintain gaps. The position is independent from any thickness.
num hexas	Create a hexa cluster with 1, 4, 8, 12, 16 or 32 hexas, which are arranged in a predefined pattern.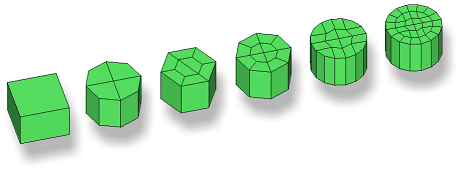 Figure 4. Note: Available for all ACM realization types.
coats	Define the number of hexa elements required along the thickness. Multiple solid coats are supported.
orthogonal faces	Force the creation of perfectly orthogonally-shaped hexas. Figure 5. . The two leftmost realizations were performed with the orthogonal faces option enabled. Note: Available for any kind of ACM weld, if num hexas is set to 1.
use rbe3 radius	RBE3 elements are typically created with three or four legs dependent on the element type (quadface, triaface) the projection of the appropriate hexa node is landing on. To be more accurate, especially regarding different mesh sizes, an rbe3 radius can be defined, so that more nodes nodes can be joined by each RBE3 element. In any case, at least one element face will be joined by each RBE3 element.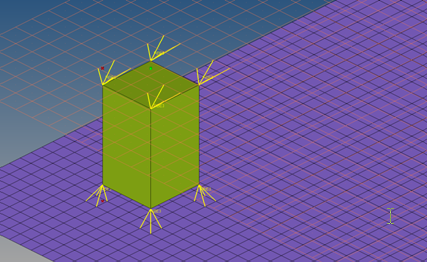 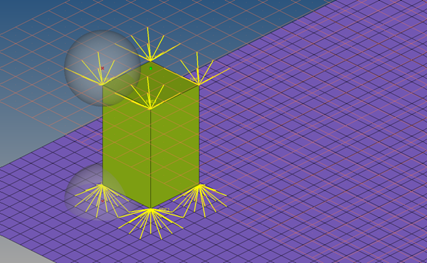Figure 6. Use Rbe3 Radius Disabled Figure 7. Use Rbe3 Radius Enabled All of the nodes of the appropriate link (outer nodes, if it is a solid link), which are positioned inside a sphere around the projection point, are considered to be joined to the RBE3 element. A feature angle is also considered. The nodes that are on a different side of the feature edge than the projection point will not be joined to the RBE3 element. When enabled you must define: rbe3 radius Define the search radius. feature center Define which projection point(s) are used as the radius center. Figure 8. Individual rbe3 Figure 9. Cluster Center weight factor Define which formula should be used for the calculation. Inverse Distribution $w_{i} = \frac{1}{r_{i}}$ Normal Distribution $w_{e i} = e^{- \frac{r_{i}^{2}}{{(0.5 \cdot r)}^{2}}}$ normalize rbe3 weights Enables the normalization of all the weights per a single rbe3. Normalized Inverse Distribution $w_{i} = \frac{\frac{1}{r_{i}}}{\sum_{i = 1}^{n} \frac{1}{r_{i}}}$ Normalized Normal Distribution $w_{e i} = \frac{e^{- \frac{r_{i}^{2}}{{(0.5 \cdot r)}^{2}}}}{\sum_{i = 1}^{n} e^{- \frac{r_{i}^{2}}{{(0.5 \cdot r)}^{2}}}}$ feature angle Define the feature angle to be considered. Note: Only available for the realization type acm (general).