Potential Material Failure Analysis

Failure Criterion

Different failure criteria can be calculated quickly and the results dynamically updated. The material failure condition is expressed by the following inequality:

Criterion Value < 1

If the inequality is met, the material is considered safe. Criterion Value depends on the stress state of the material at a given location. Safety Factor is the inverse to the Criterion Value. Dividing both sides of the inequality by the Criterion Value, one obtains the failure condition expressed through the Safety Factor:

Safety Factor = 1/Criterion Value

Note: Proper failure criterion is material and application specific. It also reflects the degree of conservatism considered appropriate for the particular design. While default criterion are provided for each SimSolid material, they should be considered as examples only. The ultimate decision of which criterion to use is the responsibility of the design engineer.

Safety Zone Contours in SimSolid

Safety zone contours are presented in 3 color bands (red, yellow and green). The threshold between bands are controlled by the Safety Factor Low and Safety Factor High values. The factors act as multipliers on the criterion value and reflect the degree of uncertainty that you are looking to tolerate. For example, a safety factor value of 1.25 indicates a 25% safety margin on the failure criterion value.

Failure Theories

Failure theories are material specific and their formulation is dependent on the type of material being considered.

Ductile Materials: In ductile materials, failure takes place by yielding. Ductile materials includes most metals and some plastics. The material tensile yield strength (TYS) is used to determine the working stress. Prior to yield, material response is assumed to be elastic.
Figure 1.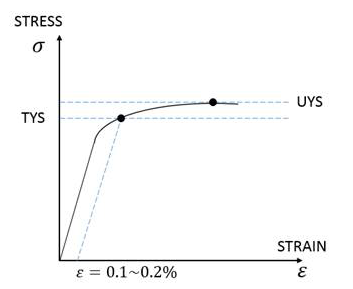

Many steels, especially heat-treated materials, do not have a well-defined elastic limit. In this case, the yield strength is usually defined at the point where the plastic strain is about 0.1% to 0.2%
CAUTION:
Steel is often thought of as a ductile material. However this is not always the case. At low temperatures on the order of 20°to 40° F (-7° to 5° C) many steels begin to lose their ductile properties. Below some transition temperature, you can no longer treat steel like a ductile material.

It is recommended that you contact the material supplier for best practices on how to determine material failure.
Brittle Materials: In brittle materials, failure takes place by fracture, therefore the criteria of failure is different from that for ductile materials. The fracture stress in compression is much larger than that in tension.
Figure 2.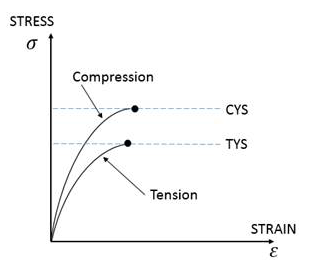

The failure theories available in SimSolid are as follows:

Max von Mises Stress: Most appropriate for ductile materials, this theory is also known as the maximum distortion energy criterion, octahedral shear stress theory or Maxwell-Huber-Hencky-von Mises theory. It is computed as the ratio of the material’s tensile yield strength to the von Mises stress and is usually considered to be the best fit with experiment results.
Max Shear Stress: Most appropriate for ductile materials, this theory is also known as Tresca's or Guest's criterion. It states that yielding begins whenever the maximum shear stress in the model becomes equal to the maximum shear stress in a tension test specimen that has begun to yield. As compared to the Max von Mises Stress theory, Max Shear Stress is a more conservative approach. In some cases, it can over-estimate stress by 15%.
Max Normal Stress: Most appropriate for brittle materials, this theory is also known as Coulomb’s criterion. It is computed by examining the ratio of the material’s tensile and compressive strength to the max principal stresses.
Christensen: This is a more recent theory that tries to bridge the gap between failure criteria for ductile and brittle materials. The Christensen failure criterion is composed of two separate subcriteria representing competitive failure mechanisms. One has a quadratic form similar to the von Mises criterion and the other is a Coordinated Fracture criterion similar to the Coulomb-Mohr criterion.

Failure Criterion Formulas

Table 1.
Criterion	Formula
Max von Mises Stress	$SF = \frac{σ_{tensile yield}}{σ_{von Mises}}$
Max Shear Stress	$SF = \frac{σ_{tensile yield}}{2 τ_{\max}}$ where: $τ_{max} = maximum (\|\frac{σ_{1} - σ_{2}}{2}\|, \|\frac{σ_{2} - σ_{3}}{2}\|, \|\frac{σ_{3} - σ_{1}}{2}\|)$
Max Normal Stress	${SF}_{i} = \frac{σ_{tensile yield}}{σ_{i}}$ if $σ_{i}$ > 0 and ${SF}_{i} = \frac{σ_{compressive yield}}{σ_{i}}$ if $σ_{i}$ < 0 for i = 1, 2, 3 $SF = minimum ({SF}_{1}, {SF}_{2}, {SF}_{3})$
Christensen	if $(\frac{σ_{tensile}}{σ_{compressive}} \leq \frac{1}{2})$ then ${SF}_{1} = \frac{σ_{tensile}}{σ_{1}}, {SF}_{2} = \frac{σ_{tensile}}{σ_{2}}, {SF}_{3} = \frac{σ_{tensile}}{σ_{3}}$ ${SF}_{4} = \frac{1}{\sqrt{E Q}}$ $SF = minimum ({SF}_{1}, {SF}_{2}, {SF}_{3}, {SF}_{4})$ where: $EQ = (\frac{1}{σ_{tensile}} - \frac{1}{σ_{compressive}}) (σ_{1} {+σ}_{2} {+σ}_{3}) + (\frac{1}{σ_{yield} σ_{compressive}}) (σ_{von Mises}^{2})$