Sheet Lamination

Analysis > Magnetostatic Loads > Sheet Lamination

Introduction

The Sheet Lamination allows to define stacked magnetic sheets and allows to compute iron losses in Transient and AC analysis (only Bertotti model at this time).

This Load enables the modeling of a laminated part: magnetic (permeability μr) non conducting, like stacked magnetic sheets simplified via the homogenization method.

It is defined by:
  • a stacking factor:

    The sheet lamination is said to be laminated because it automatically accounts for the effect of the insulation of the electrical steel and for the small air gaps between the sheets in a stack. This is achieved through a homogenization procedure implemented. The overall effect of this homogenization is that the effective cross-section of magnetic material available for the magnetic flux to traverse in the region is reduced. The reduction factor is known as the stacking factor of the region, and corresponds to the total cross section area occupied by magnetic material (steel) in the stack divided by the surface area of the geometrical cross section of the same stack (i.e., the total cross section area, including the insulation and air gaps between sheets). This definition is illustrated below:

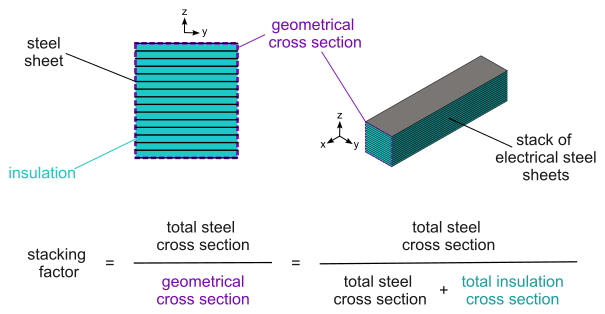
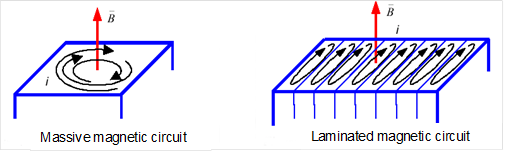
Sheet laminations are often used in magnetic circuits of transformers and of some electrical machines in order to reduce Eddy current losses. Here is an example of laminated transformer:

The eddy current distribution is shown on the following image for both Massive magnetic circuit and Laminated magnetic circuit:

In 2D, the sheet laminations are planar and each sheet is in the considered 2D plane.

Sheet Lamination Dialog Box for 2D Transient Magnetic, 2D AC Magnetic, and 2D Magnetostatic solutions

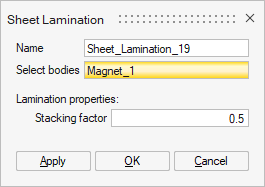
  • Select bodies: one or several bodies to define as sheet lamination.
  • Lamination properties:
    • Stacking factor

Steps

  1. Check the prerequisites:

    1. a Soft Magnetic Material should be assigned to the body. To compute the iron losses in transient and AC analysis, the Bertotti parameters should be defined.

  2. Click on the Sheet Lamination button in Analysis ribbon:

  3. Select bodies: Select one or several bodies to define as a sheet lamination.
  4. Choose the Stacking factor
  5. Validate by clicking on OK

    → The sheet lamination is created and appears in the Solution Browser in the Loads and Constraints node.