Current Density Computation Method
It is possible to set an environment variable in SimLab to change the method for the
computation of the current density 
Available methods for the current density computation
We want to compute the current density  in
solid conductors with the electric conduction model.
in
solid conductors with the electric conduction model.
 in
solid conductors with the electric conduction model.
in
solid conductors with the electric conduction model.- The first approach computes
from the result of the electric scalar potential formulation,
, with σ the electric conductivity. This formulation used nodal final elements to compute the electric scalar potential V. But this formulation does not strongly respect the conservation of the current.

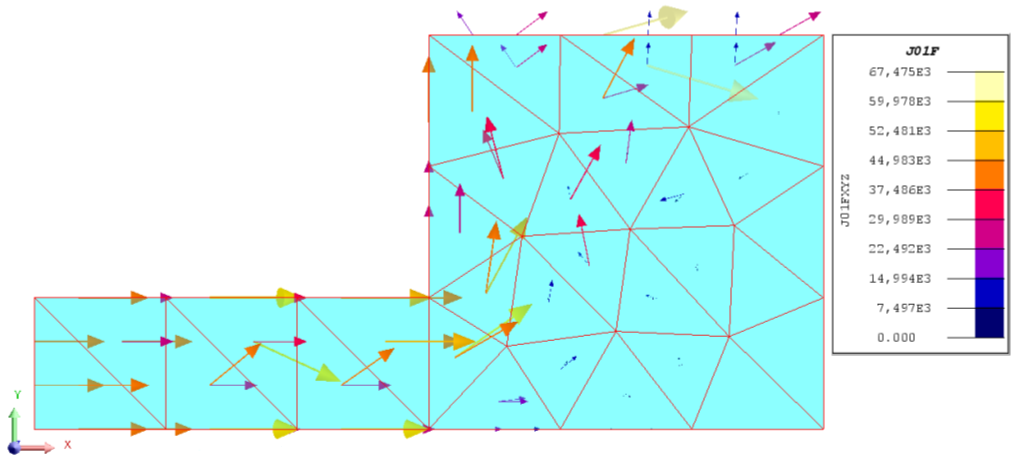
- The second approach computes the source current density
with the least square method. The source current density
uses facet finite element. This formulation respects the conservation of the current density. However, the source current density
is not unique with the least square method.
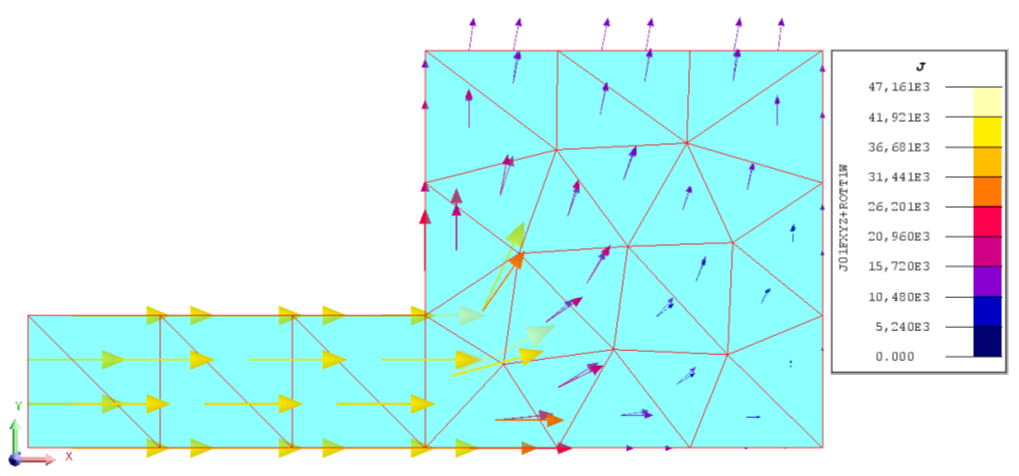
- In the third approach, the value of
is corrected by the curl of an arbitrary electric vector potential
to have a unique current density. The first step of this third approach is the same as the second approach, computing the source current density
with the least square method. The second step of finding an electric vector potential
, such that the current density is
. The electric vector potential
is computed with edge finite element. This formulation respects the conservation of the current density and has a unique solution for the current density
.
Environment variable setting
If the environment variable is not set, the current density is computed with the
first approach:
It is possible to change the computation method by defining the environment variable: SL_FLUX_J0_COMPUTATION.
There are 4 possible values:
- 0: Automatically specified method using the
first approach
- 1: Second approach computing
with the least square method using facet finite element
- 2: Third approach using the second approach at
a first step and then correcting the
by the curl of an arbitrary electric vector potential
to have a unique current density
- 3: First approach