HyperView Composite libraries expose different flavors of the
general criterion of PUCK failure theory for 2D plane stress.
Simple Puck
- Fiber Failure
-
- Where
or
if
or
- Matrix Failure
-
- Where
or
if
or
- The final failure is given as:
-
Modified Puck
- Fiber Failure
-
- Where
or
if
or
- Matrix Failure
-
- The final failure is given as:
-
Puck2D
- Fiber Failure
-
- Where
or
if
or
- Matrix Failure
- Three failures modes are developed:
- Mode A
- When
-
- Mode B
- When
and
-
- Mode C
- Otherwise
-
- Where, for all the above equations we define:
-
-
-
- Being
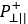 and
and 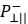 , in Puck’s theory, the inclination parameters respectively on
the tension and compression side.
, in Puck’s theory, the inclination parameters respectively on
the tension and compression side.
- The following values are used:
|
GFRP |
CFRP |
OTHERWISE |
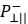 |
0.25 |
0.30 |
0.2 |
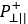 |
0.30 |
0.35 |
0.3 |
Syntax
PuckFT(tensor,xt,xc,yt,yc,s,criterion,output2d,sets,plies,elems,parts,props,pool_name,layer_index,opt_str)
Arguments
- tensor
- Stress table
- xt
- Allowable tensile stress in ply material direction 1
- xc
- Allowable compressive stress in ply material direction 1
- yt
- Allowable tensile stress in ply material direction 2
- yc
- Allowable compressive stress in ply material direction 2
- s
- Allowable in-plane shear stress
- criterion
- Puck Criterion: simple, modified, General2D, Glass2D, Carbon2D (D=simple)
- output2d
- Puck 2D output mode: value or mode (0=fiber failure, 1,2,3=matrix failure mode A,B,C)
(D=value)
- sets
- Set table (D=NULL)
- plies
- Ply table (D=NULL)
- elems
- Element table (D)
- parts
- Part table (D)
- props
- Property table (D)
- pool_name
- Pool name (D=@current_pool)
- layer_index
- Layer index (D=@current_slice_index)
- opt_str
- This is an optional argument, which can passed if needed (D=option).
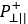 and
and 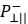 , in Puck’s theory, the inclination parameters respectively on
the tension and compression side.
, in Puck’s theory, the inclination parameters respectively on
the tension and compression side.