firls
Create a digital FIR multi-band filter with a least squares fitting.
Syntax
[b] = firls(n,f,a)
[b] = firls(n,f,a,w)
Inputs
- n
- The filter order.
- f
- A vector specifying the frequency band edges. The frequencies are normalized so that the Nyquist frequency is 1.
- a
- A vector specifying the amplitude at each frequency band edge.
- w
- A vector specifying weights, with one weight per band. The default is an unweighted fit.
Outputs
- b
- The polynomial coefficients of the filter.
Example
Plot the magnitude response for a 20th order FIR digital filter with a stop band from 200
to 250 Hz that is weighted twice as much as the pass bands, and a 1000 Hz sampling
frequency.
fs = 1000;
f = [0, 100, 200, 250, 350, 490];
a = [1,1,0,0,1,1];
w = [1,2,1];
b = firls(20, f/(fs/2), a, w);
[h,f] = freqz(b,1,[0:5:500],fs);
plot(f,abs(h));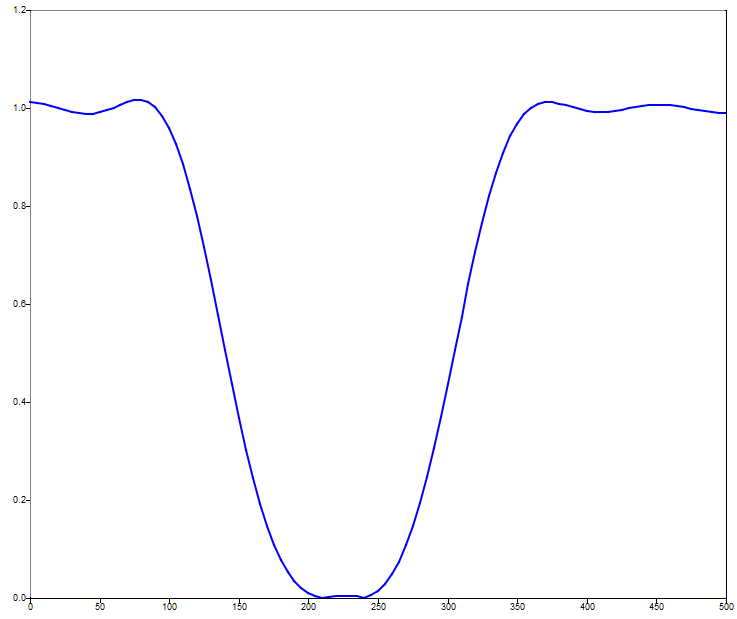
Comments
The function increments an odd order input automatically to an even number.