tfestimate
Estimates the transfer function from time domain signals.
Syntax
tfe=tfestimate(x,y)
tfe=tfestimate(x,y,window)
tfe=tfestimate(x,y,window,overlap)
tfe=tfestimate(x,y,window,overlap,nfft)
tfe=tfestimate(x,y,window,overlap,nfft,fs)
tfe=tfestimate(x,y,window,overlap,nfft,fs,range)
tfe=tfestimate(x,y,window,overlap,nfft,fs,range,'Estimator',est)
[tfe,freq]=tfestimate(...)
Inputs
- x
- The signal.
- window
- The window size, or the window vector.
- overlap
- The number of overlapping points in adjacent windows.
- nfft
- The size of the fft.
- fs
- The sampling frequency.
- range
- The spectrum type: 'onesided' or 'twosided'.
- est
- The estimator type, 'H1', 'H2' or 'H3'.
- 'est'
- The transfer function estimator.
Outputs
- tfe
- The transfer function estimate values.
- freq
- The vector of frequencies corresponding to the transfer function estimate values.
Example
Use filtered noise to estimate the magnitude response of a 4th order Butterworth filter.
fc = 100;
fs = 1000;
[b, a] = butter(4, fc/(fs/2));
rand('seed', 2019)
signal1 = randn(1, 4096);
signal2 = filter(b, a, signal1);
tfestimate(signal1, signal2, 1024, 512, [], fs);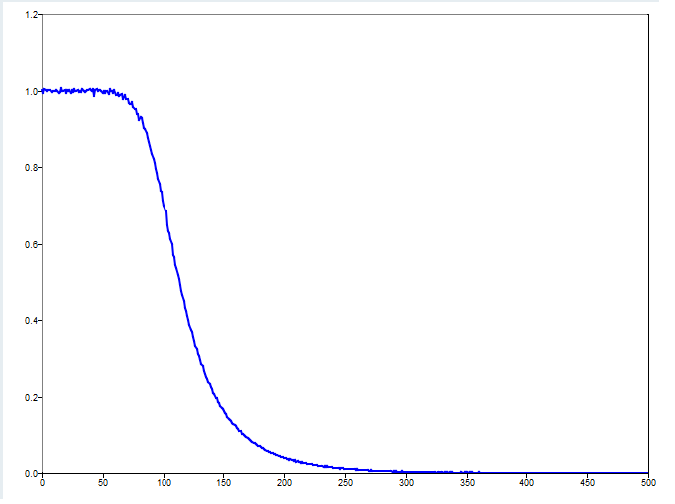
Comments
With no return arguments, the function will automatically plot the tfe magnitudes.
The 'onesided' output has a length of nfft/2+1 if nfft is even, or (nfft+1)/2 if nfft is odd.
It is often recommended to remove the signal means prior to calling tfestimate. The function does not remove the mean automatically.
- window
- A Hamming window with the largest length that produces eight data segments.
- overlap
- One half of the window length.
- nfft
- The window length. A larger value will pad zeros to each block of windowed data.
- fs
- 1.0 Hz.
- range
- 'onesided'.