trim
This command allows the user to trim a surface using a curve or set of curves.
Inline mode usage
- trim -h
- Displays the help file that summarizes the parameters for this command.
- trim –s <surface> -c <curve>
- Trims the selected surface <surface> with the selected curves <curve>.
Interactive mode usage
- Invocation
- trim
- Parameters
-
- Surface to trim.
- Cutting closed curves to be used for the trim operation.
Example
We want to create a circular hole (with radius 1) in the center of a plane. This plane is defined as follows:
>planeSelect first point [x y z]: 0 0 0Select second point [x y]: 4 4> explodeSelect objects on screen (Press enter when done) // Select the plane and press Enter.> We need to explode the plane so it will be treated as a surface and not as an object. Next, we will define our cutting curve, in this case, a circle. This is done with the following command:
>circleCenter [x y z]: 2 2 0Radius [double]: 1> 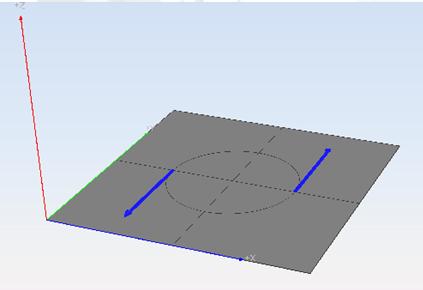
We have the surface to trim and the cutting curve, so we can proceed with the trim operation. However, the direction of the curve is going counter-clockwise (we can check this by selecting the curve and showing the normals with the Normals button on the toolbar), so the trim operation will delete the part of the plane that is outside the circle1. We want exactly the opposite, so will need to invert the normals of the circle. This can be done simply clicking on the geometry view while the normals of the curve are being shown.
Now we can finally perform the trim operation. This is done in the following way:
> trimSelect one NURBS surface to trim (Press enter when done): // Select the planeSelect cutting closed curve(s) (Press enter when done): // Select the circle>