RD-V: 0250 Concrete Validation with Kupfer Tests

Concrete validation with Kupfer tests.

Radioss includes the material models LAW24 and LAW81 to model concrete failure modeling under compression and tension. In this verification problem, the simulation results are compared to the experiment data.

Options and Keywords Used

Concrete material law (/MAT/LAW24 (CONC), /MAT/LAW81 (DPRAG_CAP))
Brick elements
Solid property (/PROP/TYPE14 (SOLID))
Boundary condition (/BCS)
Imposed displacement (/IMPDISP)
Imposed velocity (/IMPVEL)
Pressure load (/PLOAD)

Input Files

Before you begin, copy the file(s) used in this problem to your working directory.

RD-V-0250_Kupfer.zip

Model Description

A 10 mm concrete cube is modeled using one brick element with the same boundary conditions as the experimental tests.

For stability reasons, 1 element models must use a time step scale factor of 0.1.

Solid properties are:

q_a = 1.1 and q_b= 0.05 (default values)
I_solid= 24
I_frame= 2 (co-rotational formulation)
I_strain= 1 (to post-treat stains)

In this verification problem, two material laws, /MAT/LAW24 and /MAT/LAW81, will be compared to the experiment data.

The following system is used: mm, ms, g, MPa

The material data ^¹ used:

Concrete Material Law (/MAT/LAW24)
Initial density: 0.0022 $[\frac{g}{m m^{3}}]$
Concrete elasticity Young's modulus: $E_{c} = 31700 [MPa]$
Poisson's ratio: $ν = 0.22$
Concrete plasticity initial value of hardening parameter: $k_{y} = 0.35$
Concrete plasticity dilatancy factor at yield: $α_{y} = - 0.6$
Concrete plasticity dilatancy factor at failure: $α_{f} = 0.2$

Data Read Kupfer Experimental Data
Concrete uniaxial compression strength: $f_{c} = 32.22 [MPa]$
Concrete uniaxial tension strength: 0.01 $f_{c}$ , then set $\frac{f_{t}}{f_{c}} = 0.1$ (Default=0.1 in LAW24)
Concrete biaxial strength: 1.15 $f_{c}$ , then set $\frac{f_{b}}{f_{c}} = 1.15$

All other parameters can be left as default in LAW24 because the default values are representative of generic concrete materials.

Concrete Material Law (/MAT/LAW81)
Initial density: 0.0022 $[\frac{g}{m m^{3}}]$
Bulk modulus: $K = \frac{E_{c}}{3 (1 - 2 ν)} = 18869 .048[MPa]$
Young's modulus: $E_{c} = 31700 [MPa]$
Poisson's ratio: $ν = 0.22$
Shear modulus: $G = \frac{E_{c}}{2 (1 + ν)} = 12991 .8[MPa]$

The following data was calculated by curve fitting the experimental data using the Compose script, included with the input files.

Friction angle: $ϕ = 68 {.35}^{\circ}$
Ratio: $α = 0 .4186898$
Cap limit pressure set constant: $P_{b} = 0.838, f_{c} =27 [MPa]$
Cap beginning pressure: $P_{a} = α \cdot P_{b} =0 .351, f_{c} = 11.305 [MPa]$
Material cohesion set constant: $c = 0.169175, f_{c} = 5.4508 [MPa]$

Note: In this verification problem, stresses are scaled by

f_{c}

. A common practice for concrete materials is to define pressures as positive in compression. Stresses are then negative in traction or tension.

Simulation Iterations

The purpose of this verification problem is to compare the simulation results to experimental data from the Kupfer ^² tests.

Table 1. Loading and Failure
Test	Principle Stress	Triaxiality	Failure Stress
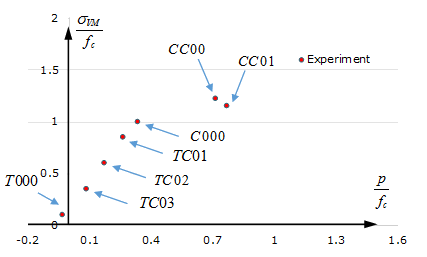
T000 Uniaxial tension	$σ_{1} = 0$ ; $σ_{2} = 0$ ; $σ_{3} = 1$	1/3	0.1 $f_{c}$
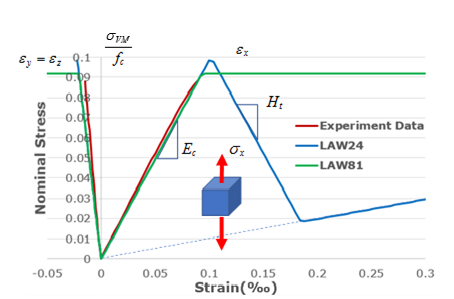
C000 Uniaxial compression	$σ_{1} = - 1$ ; $σ_{2} = 0$ ; $σ_{3} = 0$	-1/3	$f_{c}$
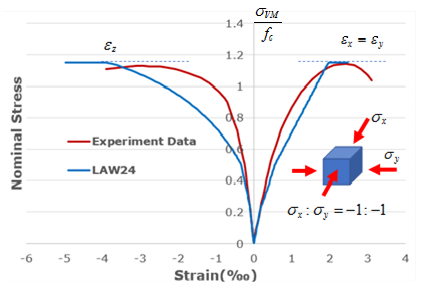
CC00 Biaxial compression	$σ_{1} = - 1$ ; $σ_{2} = - 1$ ; $σ_{3} = 0$	-2/3	1.15 $f_{c}$
CC01 Compression/Compression	$σ_{1} = - 0.52$ ; $σ_{2} = 0$ ; $σ_{3} = - 1$	-0.5849	1.22 $f_{c}$
TC01 Compression/Tension	$σ_{1} = 0.052$ ; $σ_{2} = 0$ ; $σ_{3} = - 1$	-0.3077	0.8 $f_{c}$
TC02 Compression/Tension	$σ_{1} = 0.102$ ; $σ_{2} = 0$ ; $σ_{3} = - 1$	-0.2838	0.6 $f_{c}$
TC03 Compression/Tension	$σ_{1} = 0.204$ ; $σ_{2} = 0$ ; $σ_{3} = - 1$	-0.2377	0.35 $f_{c}$

The triaxiality can be computed using the principal stresses:

σ^{*} = \frac{σ_{m}}{σ_{V M}}

with $σ_{m} = p = \frac{1}{3} (σ_{1} + σ_{2} + σ_{3})$ and $σ_{V M} = \sqrt{\frac{1}{2} [{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}]}$ .

Figure 3 shows concrete material experiment failure stress (scaled by

f_{c}

) in the

σ_{V M} versus p

stress space.

Figure 3. Experiment Data in von Mises/Pressure Curves

Results

Failure Results with LAW24 and LAW81

The failure curve in LAW24 is:

r_{f} = \frac{1}{a} (b + \sqrt{b^{2} - a (σ_{m} - c)}

With $b = \frac{1}{2} (b_{c} + b_{t})$

Radioss will curve fit Equation 2 using the different strength input

f_{c}

\frac{f_{t}}{f_{c}}

\frac{f_{b}}{f_{c}}

to generate the

r_{f}

failure curve (green).

Figure 4. Experiment Data and LAW24 Analytical Data in von Mises/Pressure Curves

The failure curve and yield curve in LAW81 are the same, and can be described in two parts:

$p \leq P_{a}$
It is linear with $p \tan ϕ + c$
The failure is $σ_{m} \tan ({68.35}^{\circ}) + 5.4508$
$P_{a} < p \leq P_{b}$ (cap)
The cap curve is:
$\sqrt{1 - {(\frac{p - p_{a}}{p_{b} - p_{a}})}^{2}} \cdot (p \tan ϕ + c)$
The failure is:
$\sqrt{1 - {(\frac{σ_{m} - 27}{27 - 11.305})}^{2}} \cdot σ_{m} \cdot \tan ({68.35}^{\circ}) + 5.4508$

These two parts of the failure curve for LAW81 are:

Figure 5. Experiment Data and LAW81 Analytical Data in von Mises/Pressure Curves

The failure results with LAW24 and LAW81 under different loading paths (from Kupfer tests) show as:

Figure 6. LAW24 Analytical and Simulation Results (load path) in von Mises/Pressure Curves

Figure 7. LAW81 Analytical and Simulation Results (load path) in von Mises/Pressure Curves

Comparing LAW24 and LAW81 failure results with experiment data, the LAW81 results are better than LAW24.

Figure 8. Experiment Data and LAW24 Radioss Results in von Mises/Pressure Curves

Figure 9. Experiment Data and LAW81 Radioss Results in von Mises/Pressure Curves

The failure results in LAW81 match the experiment data even in cap region. For the LAW24 results, most match the analytical results; except that CC00 shows a slightly larger difference analytical curve, but it is almost the same as the experiment data. The following CC00 stress-strain diagram shows almost the same failure stress.

Figure 10. CC00 Experiment Data and LAW24 Radioss Results

Results for Concrete Tension Tests

Concrete does not support very much load in tension. In LAW24 the uniaxial tensile failure (modeled by stress) and elastic modulus softening behavior is defined by $H_{t}, D_{\sup}, ε_{\max}$ . The softening modulus $H_{t} = - E_{c}$ (default) for tension is set. The peak for the above curve is at 0.1 where it is defined by $\frac{f_{t}}{f_{c}} = 0.1$ (default) in input.

In LAW81, the same bulk and shear modulus are used for tension and compression. With LAW24 it is possible to use

E = (1 - D_{\sup}) \cdot E_{c}

to represent a residual stiffness in the concrete after softening. This is not possible with LAW81.

Figure 11. Uniaxial Tension T000 Experiment Data and Radioss (LAW24 and LAW81) Results

Conclusion

Under complex loading, the concrete mechanic failure behavior is shown using two Radioss material models LAW24 and LAW81 and results compared to experiments. For LAW24 the default values are a good choice, if no experimental data is available. For LAW81, the material parameters $ϕ, c, α, P_{b}$ need to be calculated with curve fitting using at least four experimental tests.

References

¹ Han, D. J., and Wai-Fah Chen. "A nonuniform hardening plasticity model for concrete materials." Mechanics of materials 4, no. 3-4 (1985): 283-302

² Kupfer, Helmut B., and Kurt H. Gerstle. "Behavior of concrete under biaxial stresses." Journal of the Engineering Mechanics Division 99, no. 4 (1973): 853-866