EL Card
A mesh of surface triangles in the shape of an ellipsoidal section is created with the EL card.
On the Construct tab, in the Surfaces group,
click the ![]() Ellipsoid (EL) icon.
Ellipsoid (EL) icon.
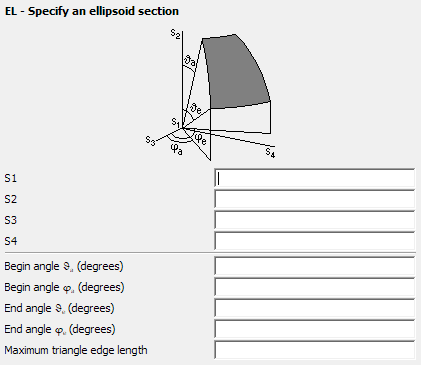
Parameters:
- S1
- The centre point of the ellipsoid.
- S2
- A point, in the direction in elliptical coordinates. The distance of the two points S1 and S2 determines the half-axis of the ellipsoid in this direction.
- S3
- A point in the direction , in elliptical coordinates. The distance of the two points S1 and S3 determines half of the axis of the ellipsoid in this direction.
- S4
- A point in the direction of the third coordinate, for example, the axes S4–S1, S3–S1 and S2–S1 must be perpendicular. The distance of the two points S1 and S4 determines half of the axis of the ellipsoid in this direction.
- Begin angle
- Start angle of the ellipsoid in degrees.
- Begin angle
- Start angle of the ellipsoid in degrees.
- End angle
- End angle of the ellipsoid in degrees.
- End angle
- End angle of the ellipsoid in degrees.
- Maximum triangle edge length
- Maximum length of the triangles along the curved edge in m (is scaled by the SF card). If this parameter is left empty, the value specified with the IP card is used.
Note that the angles and are defined in an elliptical, rather than a spherical coordinate system. For a Cartesian coordinate system with origin S1, x axis in direction of S3, y axis in the direction of S4 and z axis in the direction of S2, a point r on the surface of the ellipsoid is given as
where the lengths a, b and c are the lengths of the ellipsoid’s three half-axes. (For example the length a is the distance between the points S3 and S1).
The normal vector of the generated triangles always points outwards. The algorithm used for the segmentation can fail if the ratio of the half-axis is too extreme, for example if the longest half-axis is a factor 100 longer than the shortest. It is strongly advised to check the geometry with POSTFEKO.
Example of EL card usage
The mesh shown in Figure 2 is generated by using the EL card.