Home
Boundary Conditions
Boundary Conditions available for SimSolid.
Base Excitation

Welcome
What's New
View new features for SimSolid 2024.1.
Get Started
Learn the basics and discover the workspace.
Tutorials
Discover SimSolid functionality with interactive tutorials.
Interface with External Products
Interfaces that support SimSolid output file format.
Geometry
Information about treatment and properties of geometric entities in SimSolid.
Assembly
Summary of available functionality for defining the properties and behavior of parts in the model.
Connections
Connections are used to define the association of different regions of interest between parts in an assembly.
Create Analysis
Create an analysis for your project.
Boundary Conditions
Boundary Conditions available for SimSolid.
- Available Boundary Conditions for Analyses
  A comparison chart showing the available boundary conditions for each analysis type.
- Immovable Constraints
  Enforce zero translational displacements in all directions on faces, edges, vertexes, and/or spots.
- Slider Constraints
  Enforce zero displacement in normal to the surface direction on faces and areal spots.
- Hinge Constraints
  Allow free rotation about the centerline of cylindrical faces, and constrain movement in radial and axial directions.
- Spring Support
  Set an elastic foundation at selected faces.
- General Constraints
  Constrain displacement of faces, edges, vertices, or spots in Modal analysis.
- Alignment Constraints
- Cable Tightening/Rod Preload
  Apply shortening or change of length for cables/rods.
- Pressure
  Apply positive pressure towards a face or negative pressure outwards from a face.
- Force/Displacement
  Apply uniform loads and/or displacements to faces, edges, vertices, or spots.
- Gravity Load
  Simulate the force of gravity as it affects your model.
- Translational Inertia Load
  Apply a uniformly distributed translational inertia load over the volumes of the parts in an assembly.
- Rotational Inertia Load
  Apply a uniformly distributed rotational inertia load over the volumes of the parts in an assembly.
- Inertia Relief
  Simulate deformations and stresses in cases where you have an unconstrained structure to which an active load is suddenly applied.
- Remote Load
  Apply distributed loads (tractions) to faces, general virtual connector, or spots that are statistically equivalent to a load applied on a single point.
- Remote Displacement
  Apply displacements to faces and/or spots that are statistically equivalent to a load applied on a single point.
- Thermal Load
  Simulate deformations and stresses induced by the temperature changes in your model.
- Bearing Load
  Apply a varying pressure load to full or partial face(s) of revolution.
- Hydrostatic Pressure
  Define pressure exerted by a fluid at equilibrium.
- Distributed Mass
  Apply distributed mass across selected faces.
- Bolt/Nut Tightening Loads
  Available for blind bolts (bolt without a nut), bolt with nut/bolt on threaded rod, nut on generic post or handle.
- Base Excitation
- Volume Expansion/Shrinkage
  Apply volumetric expansion/shrinkage coefficient over seam welds or other parts in the assembly.
- Temperature
  In thermal analysis, limit temperature on the selected faces, edges, vertices, or spots to a prescribed value.
- Thermal Convection
  In thermal analysis, define a convective heat exchange condition on faces and spots.
- Surface Heat Flux
  In thermal analysis, apply uniformly distributed heat loads to faces and spots.
- Volume Heat Loads
  In thermal analysis, simulate internal heat generation and internal heat absorption in volumes.
- Solar Loads
  Apply heat loads based on the sunbeam’s direction for thermal analysis
- Wind Loads
  Theory of wind load
Post Processing
Run analyses and view a variety of results in SimSolid.
Design Study
Design studies allow you to quickly evaluate and compare the structural performance from different design scenarios.
Verification Problems
Solved verification models.
Frequently Asked Questions
This section provides quick responses to typical and frequently asked questions regarding

Base Excitation

Transient/Frequency Response

Two types of base excitations are possible. The excitation can be specified in terms of displacements or accelerations. Both are applied in the global X, Y or Z coordinate frames only.
You can select the excitation type (displacement or acceleration), time function, scaling amplitude and direction.
In addition, displacement-based excitations can be applied to individual supports which can be important for long ground-based structures like pipe systems, bridges, and transportation systems.

Random Response

The excitation can be specified in terms of accelerations. They are applied in the global X, Y or Z coordinate frames only.
You can select the excitation type (acceleration), frequency/PSD function, scaling amplitude and direction.
The Power Spectral Density (PSD) of the response, $S_{x o} (f)$ , is related to the power spectral density of the source, $S_{a} (f)$ , by:
$S_{x o} (f) = |(H_{x a} (f)| {}^{2}S_{a} (f)$
Where, $H_{x a} (f)$ is the frequency response function.
Let us take an example of base excitation as an input to a random response analysis.
The base excitation with amplitude is used to define the input for frequency response analysis, so the units of the acceleration excitation type would be any of the below highlighted units
- m/sec²
- mm/sec²
- cm/sec²
- G
- in/sec²
Units for PSD function depend on the boundary condition. In this example, as base excitation is given as acceleration, the unit for PSD is (mm/s²)²/Hz.
Figure 1.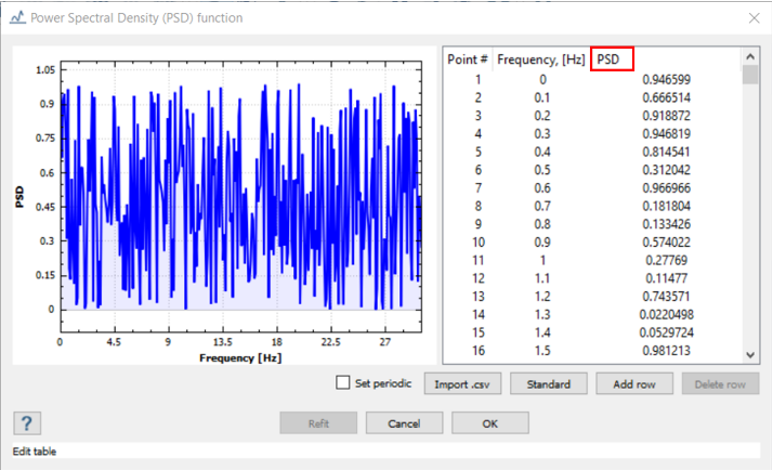

Note: Only immovable and general constraints can be used as the source location. Hinges, springs and sliders are not supported at this time.