Element Quality definitions: TET
TET element types
The quality measures supported for TET element types are as follows,
- Stretch
- Collapse Ratio
- Tet Collapse
- Skew
- Skew : Fluent
- Aspect Ratio
- Aspect Ratio : Patran
- Aspect Ratio : Nastran
- Interior Angle
- Dihedral Angle
- Volume
- Fluid - Aspect Ratio
- Edge Length
- Jacobian-Normalized
- Jacobian-Ratio
- Jacobian ABAQUS/Nastran
- Jacobian Ansys
- Height
- Stable time increment
- Boundary Tet
- Stable time increment - Radioss
- Mid node alignment ratio
- Mid node deviation ratio
- Flux: J Y Talon
- TET cleanup is supported for multiple bodies at a time.
- Preserve mesh controls applied to the body will be respected during TET cleanup.
- For bodies with Hard points mesh control, the corresponding hard nodes will be preserved in the TET cleanup.
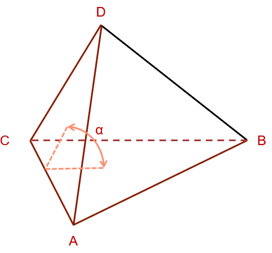
Stretch
Stretch of a TET is √24(R/L-Max), where R is the radius of the inscribed sphere and L-Max is the longest edge of the TET.
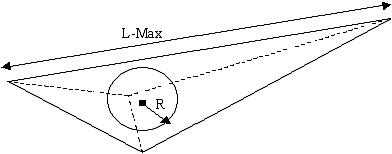
for an equilateral tetrahedron R/L-Max is 1/ √24
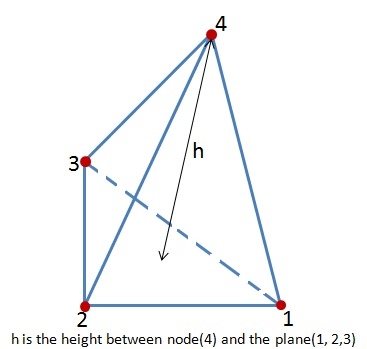
Collapse Ratio
Collapse ratio is the ratio between the smallest of the height h from each node to the longest edge of the tetrahedron. Where h is the perpendicular distance from a node to the opposite face. Collapse Ratio = h(smallest) / L(longest).
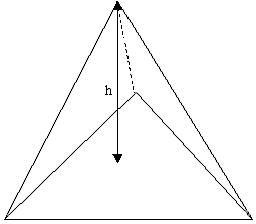
Tet Collapse
Tet Collapse of a TET element is the minimum of (h)/(1.24 √A), where h is the perpendicular distance from a node to the opposite face of the TET and A is the area of the opposite face.
Skew
Skewness of a TET element is the ratio between the volume of the TET element to the volume of an equilateral TET element with the same circumradius.
Skew: Fluent
Skew: Fluent of a TET element is calculated as, 1 minus the ratio between the volume of the TET element to the volume of an equilateral TET element with the same circumradius.
Skew: Fluent = 1 - (Volume of the Tet element / Volume of an equilateral TET element with the same circumradius)
Aspect Ratio
Aspect Ratio of a TET element is the ratio of the longest edge length to the shortest edge length.
Aspect Ratio = longest edge length / shortest edge length.
Aspect Ratio: Patran
Aspect Ratio (Patran) of a TET element is the maximum of (h)/(1.24 √A, where h is the perpendicular distance from a node to the opposite face of the TET and A is the area of the opposite face.
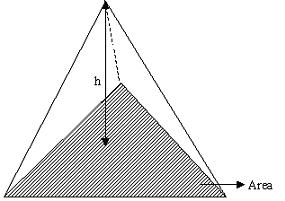
for an equilateral tetrahedron h/ √A is 1.24
Aspect Ratio: Nastran
Aspect Ratio (Nastran) of a TET element is the ratio of the longest length (edge length or height) to the shortest length (edge length or height).
Aspect Ratio (Nastran) = longest length (edge length or height) / shortest length (edge length or height)
Interior Angle
Interior Angle is the angle between the edges of a triangular face of TET. Minimum and maximum value of interior angle for each TET element is calculated by considering all the four triangular faces of the TET element.
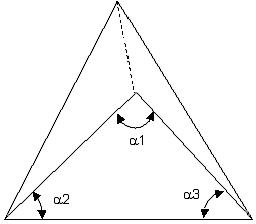
Dihedral Angle
The Dihedral Angle is the angle between the two triangular faces of TET. The Minimum and maximum value of the dihedral angle for each TET element is calculated by considering all the triangular faces of the TET element.
Volume
Volume of the TET element.
Fluid - Aspect Ratio
Fluid - Aspect Ratio is the ratio of the volume of the circumscribed sphere of the tetrahedron to volume of tetrahedron, normalised to the equilateral tetrahedron.
Edge Length
Length of Tet Edges.
Jacobian-Normalized
Jacobian Normalized is the ratio between the smallest determinant of the Jacobian matrix at corner and mid points of TET10 to the volume of the TET. For TET4 elements the Jacobian is flagged as “-1” if the element volume is less than or equal to zero and “1” for element with volume greater than zero.
Jacobian-Ratio
Jacobian Ratio is the ratio between the smallest determinant of the Jacobian matrix to largest determinant of the Jacobian matrix at gauss points based on 5 point Integration Rule.
Jacobian ABAQUS/Nastran
Jacobian ABAQUS/Nastran is the ratio between the smallest determinant of the Jacobian matrix based on 11 point Integration Rule to the volume of Tet, which is made to compatible w.r.t Both Abaqus and Nastran. To pass the failure criteria the value should be greater than zero.Jacobian Ansys
Jacobian Ansys is the ratio between the smallest determinant of the Jacobian matrix to largest determinant of the Jacobian matrix at corner nodes which is more stricter than at gauss points. For Agressive solving the value should be greater than 0.033333.
Height
Height is the perpendicular distance from a node to the opposite face of the TET
Stable time increment
The Stable time step is the time needed for a shock wave (stress / pressure wave) to cross the smallest distance in an element. It is used to determine the initial minimum time step required for explicit dynamic analysis. This parameter also depends on the material properties assigned to the elements apart from the element dimensions.
Boundary Tet
Boundary tet refers to the element that has either all of its corner nodes on the surface or any one of its interior edge having both its corner nodes on surface. In flow analysis, these elements will not participate in the flow.
Stable time increment - Radioss
The Stable time step is the time needed for a shock wave (stress / pressure wave) to cross the smallest distance in an element. It is used to determine the initial minimum time step required for explicit dynamic analysis. This parameter also depends on the material properties (Young's modulus and Density) assigned to the elements apart from the element dimensions.
Mid node alignment ratio
It describes how close a mid node can be displaced towards corner node along element edge.

Mid node deviation ratio
It describes how far a mid node is displaced from the line joining corner nodes.

Flux: J Y Talon
The J Y Talon element quality is based on the ratio between the volume of the inscribed sphere and the volume of TET.
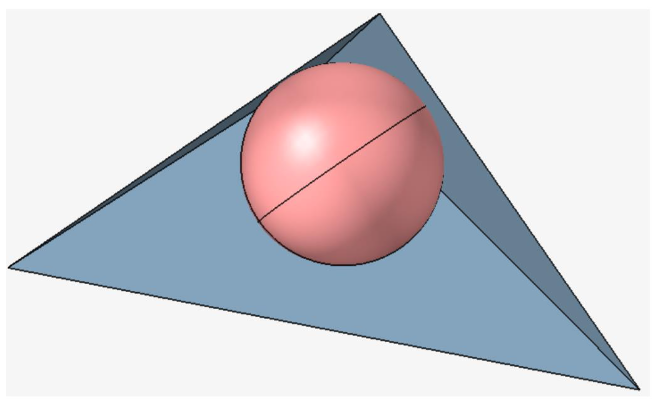
We compute the following quality value:
Q = 1- (R/Re)
Where,
Re is the ratio for an equilateral TET.
R is the ratio for the analyzed TET
For an equilateral TET, this value is equal to 0. For a flat TET, this value is close to 1. By default, for Flux solver, we consider a TET to be of satisfactory quality if Q is less than or equal to 0.8.