Labyrinth Seal Tooth by Tooth Element

Description

The Labyrinth Seal Tooth by Tooth (TbT) element is typically used to model leakage flow through labyrinth seals found in rotating machinery (gas turbines). The flow rate, swirl, and fluid temperature rise, due to windage, are calculated based on the seal geometry and fluid conditions at the inlet and exit of the seal.

This element's main feature is that it performs a tooth by tooth marching along the flow direction to calculate the pressure distribution inside the seal. It also takes into account local (in-pocket) changes in fluid properties due to changes in pressure and temperature, thus providing a more detailed modeling of the labyrinth seals.

The seal clearance is the main dimension that controls the flow rate passing through the seal. It is the distance between the tip of the seal tooth and the opposite surface, which is usually honeycomb. The seal clearance changes during gas turbine operations since the parts move due to temperature and rotation. With the labyrinth seal TbT element, you can input individual seal clearances for every tooth in the seal and study their impact on leakage.

The element is typically used for compressible flow, but Flow Simulatoralso uses this element with incompressible or compressible fluid.

Create a Lab Seal TbT

Go to Compressible Gas Elements > Seals to select the Lab Seal Tooth by Tooth element.

The figure below shows the geometric inputs. The seal clearance and seal geometry are the major inputs. Besides this, you must enter honeycomb information.

A labyrinth seal typically has the seal teeth rotating. This requires you to enter an RPM reference condition in the Solution Panel.

Labyrinth TbT Seal Inputs

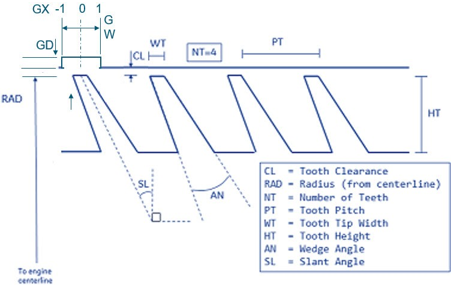
The inputs for the labyrinth TbT seal are listed below. See the image in the user interface to understand the geometric variables.


Labyrinth Seal TbT Element Input Variables
Index	UIName (*.flo label)	Description
1	Seal Clearance (CL)	Seal clearance. This can be averaged or tooth by tooth).
2	Nominal Seal Radius or Inlet Radius (RAD)	Nominal seal radius for a straight seal or the inlet radius for a stepped seal. It can be a constant for the entire seal or vary tooth by tooth. The constant value provided is assigned to every tooth in the seal. Tooth by tooth radius values can be provided in a table. The application writes the flag "-999" to the *.flo file if table entries exist. Every pocket is identified as either straight or stepped based on the individual tooth radius.
3	Number of Teeth (NT)	Number of teeth in the seal.
4	Seal Axial Pitch (PT)	Seal axial pitch. It can be a constant for the entire seal or vary pocket by pocket. The constant value provided is assigned to every tooth in the seal. Pocket by pocket pitch values can be provided in a table. The application writes the flag "-999" to the *.flo file if table entries are present.
5	Tooth Tip Width (WT)	Axial width of seal tooth tip. It can be a constant for the entire seal or vary tooth by tooth. The constant value provided is assigned to every tooth in the seal. Tooth by tooth width values can be provided in a table. The application writes the flag "-999" to the *.flo file if table entries exist.
6	Seal Tooth Height (HT)	Seal tooth height. This variable influence only the windage calculated for a rotating seal. It can be a constant for the entire seal or vary tooth by tooth. The constant value provided is assigned to every tooth in the seal. Tooth by tooth height values can be provided in a table. The application writes the flag "-999" to the *.flo file if table entries exist.
7	Wedge Angle (AN)	Angle between sides of a seal tooth. It can be a constant for the entire seal or vary tooth by tooth. The constant value provided is assigned to every tooth in the seal. Tooth by tooth wedge angle values can be provided in a table. The application writes the flag "-999" to *.flo file if table entries exist.
8	Rotor Surf. Rot. Speed (RPMSELR)	Rotational speed pointer of seal rotor surface. 0.0: Specifies a stationary element. 1.0: Points to general data ELERPM(1). 2.0: Points to general data ELERPM(2). 3.0: Points to general data ELERPM(3).


Index	UIName (*.flo label)	Description
9	Slant Angle (SL)	Angle the tooth centerline makes with the radial direction. Positive angle if tooth is angled into the flow and negative angle if slanted away from the flow. It can be a constant for the entire seal or vary tooth by tooth. The constant value provided is assigned to every tooth in the seal. Tooth by tooth slant angle values can be provided in a table. The application writes the flag "-999" to the *.flo file if table entries exist.
10	Land Surf. Rot. Speed (RPMSELL)	Rotational speed pointer of seal land surface. 0.0: Specifies a stationary element. 1.0: Points to general data ELERPM(1). 2.0: Points to general data ELERPM(2). 3.0: Points to general data ELERPM(3).
11	BASE_EQUATION	BASE EQUATION is the user dependent choice for pressure calculation formula in tooth by tooth marching: 0: Saikishan-Morrison Base Equation. 1: Neumann Base Equation. 2: Compressible Flow Function. The details of these base equations are provided in the Theory Section.
12	Portion of Ustrm Cham. Dyn. Head Lost (DQ_IN)	Inlet dynamic head loss. If DQIN ≥ 0 and the upstream chamber has a positive component of relative velocity aligned with the axis of the tube, the driving pressure is reduced by the equation. The default value of -1.0 is interpreted by Flow Simulator as a flag to use only static pressure if the upstream chamber is an inertial chamber and a DQ_IN of 0 if the upstream chamber is a momentum chamber.
13	Element Alignment (AXIS_DIR)	Direction of positive flow through the seal. If AXIS_DIR ≥ 0, the axial direction for positive flow is assumed to be the direction defined by THETA = 0, PHI = 0. If AXIS_DIR < 0, the axial direction for positive flow is assumed to be the direction defined by THETA = 180, PHI = 0.
14	Laminar-Transitional Reynolds Number (RE_LAM)	Reynolds number below which pocket swirl flow is assumed to be laminar. Flow at Reynolds numbers between RE_LAM and RE_TURB are assumed to be in the transition region. Defaults to 2070 for Labyrinth Seal.
15	Turbulent-Transitional Reynolds Number (RE_TURB)	Reynolds number above which pocket swirl flow is assumed to be turbulent. Flow at Reynolds numbers between RE_LAM and RE_TURB are assumed to be in the transition region. Defaults to 2530 for Labyrinth Seal.
16	Clearance Factor Method (KFAC_METHOD)	0: Bell-Bergelin curve for CD of annular orifice. 1: Bell-Bergelin Advanced, Table Lookup for multiple Re (Default). -1: User supplies their own KFAC, either constant value or calculated using controllers. See KFAC details below.
17	Kinetic Energy Carryover Method (KE_METHOD)	0: Vermes 1961 Kinetic Energy Carryover curve. 1: Morrison Kinetic Energy Carryover curve. 2: Minimum of Vermes and Morrison curves (default, matches NASA Tipton data best). 3: Saikishan-Morrison. 4: Neumann Kinetic Energy Carryover curve. 5: Stepped Kinetic Energy Carryover. 6: Auto. -1: User-supplied KEMULT, either constant value or calculated using controllers. See KEMULT details below.


Index	UIName (*.flo label)	Description
18	Honeycomb Method (HC_METHOD)	1: Auto, Tipton/Schramm Method (Default) – Tipton for Straight Seals, Schramm for Stepped Seals. 2: Stocker curve for straight seals. 3: Schramm curve for stepped seals. 4: Tipton table lookup for straight seals. -1: User-supplied HCMULT, either constant value or calculated using controllers. See HCMULT details below.
19	Slanted Teeth Method (SL_METHOD)	1:Curve fitted to NASA Tipton data. -1:User supplies their own SLMULT, either constant value or calculated using controllers. See SLMULT details below. 2: Auto. 3: Stepped slanted tooth factor.
20	Honeycomb Size (HCSIZE)	Honeycomb Size – Standard choices are 1/32”, 1/16”, and 1/8”. However, it is possible to input a custom honeycomb size. Solver units are inches.
21	Clearance Factor(KFAC)	Clearance factor is the Discharge Coefficient of a single annular orifice or tooth gap. The value is between 0 and 1, usually between 0.6 and 0.9. See Vermes 1961 or Bell-Bergelin.
22	Kinetic Energy Carryover Factor (KEMULT)	Kinetic Energy Carryover Factor is a value from 1 to about 2.4. It accounts for axial momentum and energy that is retained as flow goes around a tooth. A value of 1 means the tooth blocked all kinetic energy. A value higher than 1 implies some kinetic energy was carried over. Please see Vermes 1961, Morrison, and Alexiou for details.
23	Honeycomb Flow Multiplier (HCMULT)	Honeycomb Flow Knockdown Factor is a multiplier that is applied to non-honeycomb leakage flow to calculate the corrected leakage flow with a honeycomb stator. Typical values are from 0.8 to 1.2. Values less than one imply the honeycomb is supplying an additional source of resistance, which is often true for straight seals. Values greater than one imply that the honeycomb is creating a new path for leakage flow, which is often true for stepped seals. Please see Stocker and Schramm for additional details.
24	Slant Flow Multiplier (SLMULT)	Slanted Teeth Flow Knockdown Factor is a multiplier that is applied to straight-tooth leakage flow to calculate the corrected leakage flow with slanted teeth. Typical values are from 0.85 to 1.1. Three-dimension flows in seal pockets are complex, and it is difficult to explain why the factor is sometimes less than one and sometimes greater.
25	Swirl Carryover Factor per Tooth (ETATOOTH)	Swirl Carryover per Tooth is the fraction of tangential fluid velocity(relative to the stator) that passes each tooth and enters the next pocket. This is a calibration parameter that helps to match the correct swirl and windage heating. It is especially useful for stepped honeycomb seals where the air passes over the tooth and immediately impinges on the honeycomb step. It can be a constant for the entire seal or vary tooth by tooth. The constant value provided is assigned to every tooth in the seal. Tooth by tooth swirl carryover values can be provided in a table. The application writes tbe flag "-999" to the *.flo file if table entries exist.


Index	UIName (*.flo label)	Description
26	Friction and Windage – Rotor: Friction Relation (FRIC_REL_R)	0: Swamee-Jain Approximation to Colebrook-White-Moody Friction (Default). 1: MacGreehan-Ko Rotating Cavity/Pocket Friction. 5: Sultanian. -1: User-supplied FRICF_STATOR, either constant value or calculated using controllers. See FRICF_STATOR details below.
27	Rotor Sandgrain Roughness (ROUGH_ROTOR)	Roughness of the rotor surface. It is assumed to be a sand-grain type roughness, which is consistent with Colebrook-White-Moody.
28	Friction and Windage – Rotor: Friction Multiplier (F_MULT_ROTOR)	Friction multiplier on Rotor is used if you want the friction curve to follow that same basic trend as Swamee-Jain or MacGreehan-Ko but your custom friction curve differs by a multiplication factor.
29	Friction and Windage – Rotor: Friction Coefficient (FRICF_ROTOR)	Fanning Friction Coefficient on Rotor can be supplied as a constant value, or it can be calculated using a controller.
30	Friction and Windage – Rotor: Total Rotor Surface Area (ASR)	Generally, ASR=0 and the rotor friction area is calculated from other geometric inputs such as tooth height, spacing, wedge angle, slant angle, etc. If you enter a non-zero value, your input overrides the calculated area. Solver units are sq. in.
31	Friction and Windage – Stator: Friction Relation (FRIC_REL_S)	0: Swamee-Jain Approximation to Colebrook-White-Moody Friction (Default). 1: MacGreehan-Ko Rotating Cavity/Pocket Friction. 5: Sultanian. -1: User-supplied FRICF_STATOR, either constant value or calculated using controllers. See FRICF_STATOR details below.
32	Stator Sandgrain Roughness (ROUGH_STATOR)	Roughness of the stator surface. It is assumed to be a sand-grain type roughness, which is consistent with Colebrook-White-Moody. Estimating a suitable roughness for a honeycomb surface is one challenge, but no advice can be given here.
33	Friction and Windage – Stator: Friction Multiplier (F_MULT_STATOR)	Friction multiplier on Stator is used if you want the friction curve to follow that same basic trend as Swamee-Jain or MacGreehan-Ko but your custom friction curve differs by a multiplication factor.


Index	UIName (*.flo label)	Description
34	Friction and Windage – Stator: Friction Coefficient (FRICF_STATOR)	Fanning Friction Coefficient on Stator can be supplied as a constant value, or it can be calculated using a controller.
35	Friction and Windage – Stator: Total Land Surface Area (ASS)	Generally, ASR=0 and the rotor friction area is calculated from other geometric inputs such as tooth height, spacing, wedge angle, slant angle, etc. If you enter a non-zero value, your input will override the calculated area. This is especially useful for stepped seals, since the current lab Seal element does not have a step height input. However, it could be better to ignore the step height and rely on ETATOOTH – please see above. Solver units are sq. in.
36	(CL_TABLE)	Number of entries in the CL_VALUES table.
37	Groove Depth (GRV_DEPTH)	Depth of the groove (GD) in the honeycomb (or other land material).
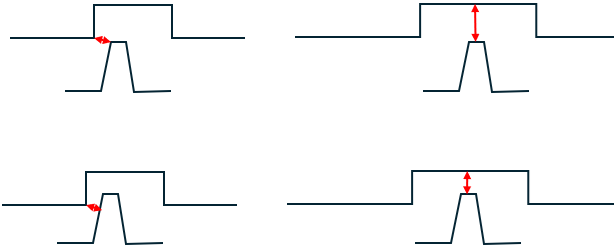
38	Groove Width (GRV_WIDTH)	Width of the groove (GW) in the honeycomb (or other land material).
39	Groove Tooth Axial Position (GRV_AX)	Location of the tooth in the groove. 0 = tooth in the center of the groove. -1 = tooth hitting left edge of groove1 = tooth hitting right edge of groove. Not used in built-in methods yet but can be useful for controller or custom groove loss correlations.
40	Groove Multiplier (GRV_MULT)	Groove Flow Knockdown Factor is a multiplier that is applied to a no-groove leakage flow to calculate the leakage flow with a groove. Can be greater or less than 1. If the tooth is outside the groove, GRV_MULT should be > 1 indicating more flow through the seal.
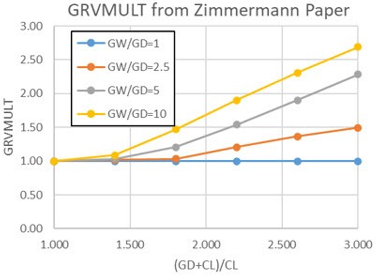
41	Groove Method (GRV_METHOD)	Method to use to calculate the groove effect. -1= User Specified GRV_MULT 1 = Zimmerman Method.
42	User Multiplier (USRMULT)	A user supplied flow knockdown factor. Can be used with a controller for general purpose effects if needed.


Index	UIName (*.flo label)	Description
43	Exit Radius (RAD_EX)	The exit radius for a stepped seal.
44	Pocket Heat Transfer Option – Rotor (HTOPT_ROTOR)	The heat transfer option to use on the rotor surface in each pocket. 0: No Heat Transfer (default) 1: Heat Transfer ON with a constant HTC 2: Heat Transfer ON with a constant Q >1000: Heat Transfer ON with a custom HTC correlation (ROTATING_CAVITY_NU)
45	Pocket Heat Transfer Option – Stator (HTOPT_STATOR)	The heat transfer option to use on the stator surface in each pocket. Same options as rotor surface of pocket.
Table1	Individual Tooth Clearances (CL_VALUES)	There is an option to provide an array of individual clearance values, one for each seal tooth.
HTC or Q Tables	(ROTOR_PKT_HTC_OR_Q), (STATOR_PKT_HTC_OR_Q)	A constant Heat Transfer Coefficient (HTC), BTU/(hr ft^2 F) or constant heat addition (Btu/sec). Separate tables for Rotor and Stator. One entry for each pocket. The table only exists when needed for the heat transfer option. No table if there is no heat transfer.
Wall Temperature Tables	(ROTOR_PKT_TWALL), (STATOR_PKT TWALL)	The wall temperature to us pocket heat transfer (deg F). Separate tables for Rotor and Stator. One entry for each pocket. The table only exists when needed for the heat transfer option. No table if there is no heat transfer.
Table 2	Individual Tooth Swirl Carryover	An array of the individual tooth swirl carryover, one for each seal tooth.
Table 3	Individual Tooth Radius	An array of the individual tooth radius, one for each tooth.
Table 4	Individual Tooth Width	An array of the individual tooth width, one for each tooth.
Table 5	Individual Pocket Pitch	An array of the individual pocket pitch, one for each pocket.
Table 6	Individual Tooth Height	An array of the individual tooth height, one for each tooth.
Table 7	Individual Tooth Slant Angle	An array of the individual tooth slant angle, one for each tooth.
Table 8	Individual Tooth Wedge Angle	An array of the individual tooth wedge angle, one for each tooth.

Labyrinth Seal TbT Element Theory

Flow Rate Calculation Base Equations.

0. The Saikishan Morrison Base Equation:
The Saikishan Morrison equation (Ref 2) used to calculate the flow rate across the n^th tooth is defined as:
$\dot{m} = A_{n} * C_{d n} * Y_{n} * \sqrt{2 * ρ_{n} * (P_{n} - P_{n + 1})}$
Where,
$\dot{m}$ = Mass flow rate across the n^th tooth.
$C_{d n}$ = Discharge coefficient across the n^th tooth.
$A_{n}$ = Geometrical flow area through the clearance.
$Y_{n}$ = Expansion factor accounting for fluid expansion after coming out of the tooth gap.
$ρ_{n}$ = Density of the fluid at the upstream pocket of the tooth.
$P_{n}$ = Pressure at the upstream pocket of the tooth.
$P_{n + 1}$ = Pressure at the downstream pocket of the tooth.
$A_{n}$ is the geometrical flow area:
$A_{n} = 2 π * (R_{t o o t h T i p} + \frac{C L}{2}) * C L$
The expansion factor as per Saikishan Morrison is given as:
For compressible flow:
$Y_{n} = 0.558 * (\frac{P_{n + 1}}{P_{n}}) + 0.442$
For incompressible flow:
$Y_{n} = 1$
The discharge coefficient for $C_{d n}$ , for the n^th tooth, is written as:
$C_{d n} = {(K F A C)}_{n} * {(K E M U L T)}_{n} * {(H C M U L T)}_{n} * {(S L M U L T)}_{n} * {(G R V M U L T)}_{n} * {(U S E R M U L T)}_{n}$
These factors are described in the section Leakage Flow Factors. Calculating these factors for any n^th tooth incorporates the corresponding tooth geometry.
1. The Neumann Base Equation:
The Neumann Base equation (Ref 10) used to calculate the flow rate across the n^th tooth is defined as:
$\dot{m} = A_{n} * C_{d n} * \sqrt{\frac{P_{n}^{2} - P_{n + 1}^{2}}{R_{n} T_{n}}}$
Where,
$\dot{m}$ = Mass flow rate across the n^th tooth.
$C_{d n}$ = Discharge coefficient across the n^th tooth.
$A_{n}$ = Geometrical flow area through the clearance.
$T_{n}$ = Temperature of fluid at the upstream pocket of the tooth.
$R_{n}$ = Gas constant of fluid at the upstream pocket of the tooth.
$P_{n}$ = Pressure at the upstream pocket of the tooth.
$P_{n + 1}$ = Pressure at the downstream pocket of the tooth.
2. The Compressible Flow Function:
The Compressible Flow function used to calculate the flow rate across the n^th tooth is defined as:
$\dot{m} = \frac{X M B X * C_{d n} * A_{n} * P_{t u p}}{\sqrt{T_{t u p}}}$
Where, $X M B X$ is the total flow parameter, and,
$X M B X = \sqrt{\frac{γ g_{c}}{R}} \frac{M N}{{(1 + \frac{γ - 1}{2} M N^{2})}^{\frac{γ + 1}{2 (γ - 1)}}}$
$M N = \sqrt{\frac{2}{γ - 1} {(\frac{P_{t u p}}{P_{s d n}})}^{\frac{γ - 1}{γ}} - 1}$
Where,
$T_{t u p}$ = Temperature of the fluid at the upstream pocket of the tooth.
$C_{d n}$ = Discharge coefficient across the n^th tooth.
$A_{n}$ = Geometrical Flow area through the clearance.
$R$ = Gas constant of the fluid at the upstream pocket of the tooth.
$γ$ = Specific heat ratio of the fluid at the upstream pocket of the tooth.
$P_{t u p}$ = Total pressure at the upstream pocket of the tooth.
$g_{c}$ = Gravitational constant.

Leakage Flow Factors

KEMULT

KEMULT is the kinetic energy carryover factor. There are eight options for the kinetic energy carryover.

0. Vermes
1. Morrison (Ref 2, eq 5)
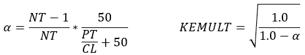
2. Vermes-Morrison
Use the minimum alpha from 1 and 2.
3. SAIKISHAN_MORRISON (Ref 2, eq 7).
This method uses the flow Re to calculate the KEMULT. Since the flow Re depends on the flow through the seal, this method uses the flow from the previous iteration.
4. Neumann (Ref 10)

$α = 1 - \frac{1}{{(1 + 16.6 * \frac{C L}{P T})}^{2}}$

$K E M U L T = \sqrt{\frac{N T}{N T * (1 - α) + α}}$
5. Stepped Kinetic Energy Carryover
KEMULT = 1.0
6. Auto
The Auto method uses the recommended Neumann Kinetic Energy carryover for straight pockets, and Stepped Kinetic Energy Carryover for stepped pockets. This is the default option.
Note: For the first tooth of a stepped seal, there is no pocket upstream, hence the Auto method applies the recommended straight correlation for the first tooth.
7. User-specified KEMULT
You can enter your own Kinetic Energy Carryover. The application writes a flag (-1) when you input a Kinetic Energy Carryover.

KFAC

KFAC, or clearance factor, is equivalent to the Vermes K variable that accounts for the effect of the ratio of seal tooth tip width to the seal clearance. There are five options:

0. Bell-Bergelin (Ref 3)
The value used approximates the data shown in Figure 2 of the Vermes paper (also from Bell-Bergelin, ref. 3) and is given by the equation:
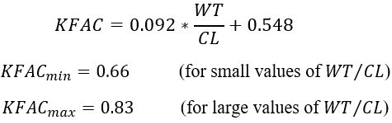
1. Bell-Bergelin Advanced. Uses a table of KFAC vs WT/CL for several Reynolds numbers from Ref. 3. Bilinear interpolation used to find KFAC. The Bell-Bergelin equation shown above matches the Re = 10,000 curve. The Advanced option is more accurate for Re < 10,000. Re is the annular orifice (tooth gap) Reynolds number and can be found in the *.res file.
Figure 4.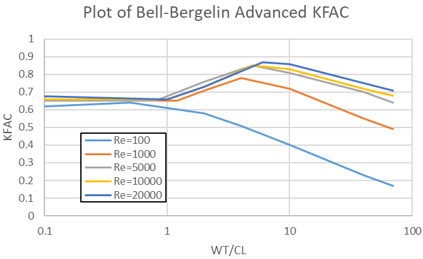
2. Saikishan Morrison KFAC
It uses the Clearance factor from the Saikishan Morrison paper (Ref 2). The factor described as the CD for first tooth is treated as KFAC here. Since the Saikishan Morrison formulation corresponds to straight and smooth seals, the CD for the first tooth has only two components, KEMULT and KFAC. KEMULT = 1.0 for the first tooth. As per Saikishan Morrison, the KFAC is written as:
For the first tooth,
$C_{d 1} = K F A C_{1} = \frac{(0.7757 - 0.002051 * (\frac{W T}{C L}))}{{(1 + \frac{44.86 (\frac{W T}{C L})}{R E})}^{0.2157}}$
For subsequent teeth,
$K F A C_{} = K F A C_{1} * 0.925 * {(K E M U L T)}^{0.861}$
3. Neumann KFAC
Neumann KFAC is the clearance factor as described in the Ref 10. It takes into account the pressure ratio at upstream and downstream of the tooth. Neumann KFAC is given by following equation:
$K F A C = \frac{π}{π + 2 - 5 β_{n} + 2 β_{n}^{2}}$
$β = {(\frac{P_{n}}{P_{n + 1}})}^{\frac{γ - 1}{γ}} - 1$
Where,
$γ$ is the specific heat ratio at the upstream pockets.

SLMULT

Auto.
The Auto method uses the recommended NASA Tipton Fitted Curve for straight teeth pockets, and the Stepped Slanted Tooth Factor for stepped teeth pockets. This is the default option.
Note: For the first tooth of a stepped seal, there is no pocket upstream, hence the Auto method applies the recommended straight correlation for the first tooth.
Stepped Slanted Tooth Factor.
SLMULT = 1.0.
User Specified.
You can enter your own Slanted Tooth Factor. The application writes a flag (-1) when you input a Slanted Tooth Factor.

HCMULT

The honeycomb flow multiplier has five options.

Auto.
The Auto method uses the recommended Tipton Straight HC curve for straight teeth pockets, and the Schramm Stepped for stepped teeth pockets. This is the default.
Note: For the first tooth of a stepped seal, there is no pocket upstream, hence the Auto method applies the recommended straight correlation for the first tooth.
Schramm Stepped Seal (Ref 4, Fig 12).

$H C M U L T = 1.0 + \frac{0.0794 - 0.1208 * \frac{W T}{H C}}{{(\frac{C L}{H C})}^{2}}$
Stocker Straight (Ref 4, Fig 12).

$H C M U L T = 1.0 + \frac{0.0794 - 0.1208 * \frac{W T}{H C}}{{(\frac{C L}{H C})}^{2}} * e^{(\frac{- 0.1725}{(\frac{C L}{H C})^.6846})}$
Tipton Straight (Ref 7, Fig 26).
An HCMULT is calculated using a bilinear interpolation of the curves shown here.
Figure 5.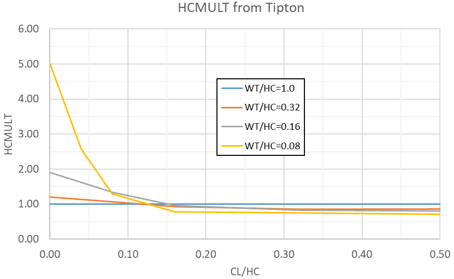
User Specified.

GVRMULT

The flow knockdown factor due to a groove in the honeycomb.

There are two options:

-1: User Specified
1: Based on Zimmerman (Fig. 7 in Ref 8).

Figure 6.

The groove width/groove depth (GW/GD) is limited in the solver to between 1 and 10. The (groove depth + clearance)/clearance ((GD+CL)/CL) is limited in the solver to between 1 and 3. Valid for Re>5000, GW/GD>2.5, but correlation uses GW/GD=1 curve also.

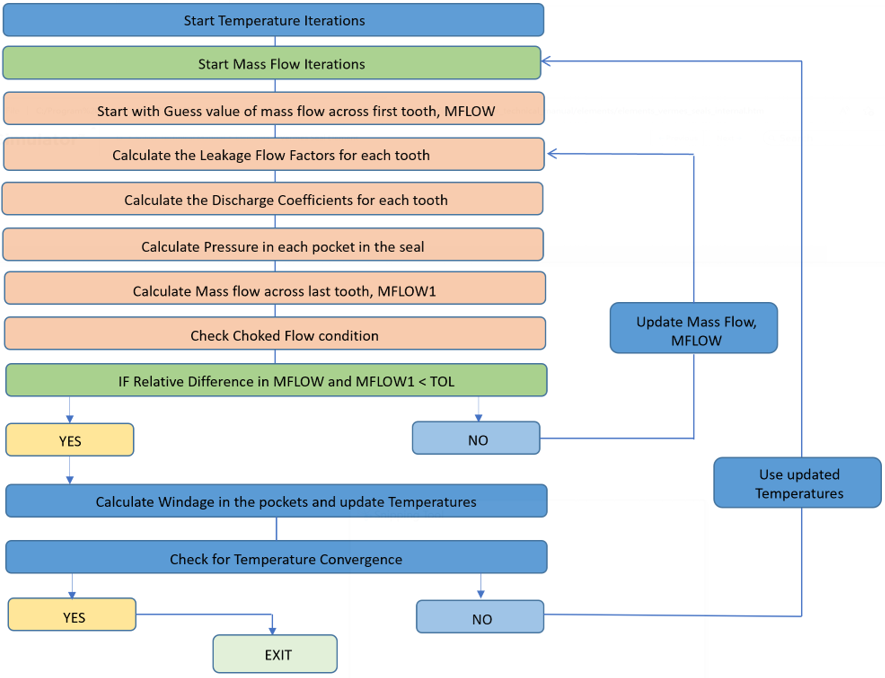
Choked Flow Calculation

For compressible gases, the calculated seal mass flow is compared to the mass flow for choked flow through the last tooth. If the choked flow through the last tooth is less than the calculated seal mass flow, the choked flow is used. The equations for the choked flow calculation are:

{\dot{m}}_{c h o k e} = \frac{C d * A r e a_{l a s t - t o o t h} * P_{l a s t - p o c k e t} * f l o w_f u n c t i o n_{c h o k e}}{\sqrt{T t_{l a s t - p o c k e t}}}

f l o w_f u n c t i o n_{c h o k e} = \sqrt{\frac{γ}{R}} \sqrt{{(1 + \frac{γ - 1}{2})}^{\frac{γ + 1}{1 - γ}}}

Where, $C d = max (1.0 a n d H C m u l t)$

This accounts for the additional flow area if the honeycomb cell allows the seal to flow more than a smooth surface (HCMULT > 1 if clearance is small and HC size is large).

Calculating Seal Pocket Pressure

Use Saikishan Morrison Base Equation, rearranging Equation 1:
$P_{n + 1}^{} = P_{n} - \frac{1}{2 * ρ_{n}} * {(\frac{\dot{m}}{A_{n} * C_{d n} * Y_{n}})}^{2}$
Use Neumann base equation, rearranging Equation 5:
$P_{n + 1}^{2} = P_{n}^{2} - R_{n} * T_{n} * {(\frac{\dot{m}}{A_{n} * C_{d n}})}^{2}$
Use Compressible Flow Function
For the Compressible Flow function, the mass flow rate across the first tooth is used to calculate the pressure ratio across the subsequent teeth (using Equation 6). At the last tooth, however, the pressure ratio is known after the tooth by tooth marching is complete for that iteration, therefore the pressure ratio is used in Equation 6 and the mass flow across last tooth is determined. At convergence, the relative difference between the mass flow across the first tooth and last tooth becomes smaller and smaller.

Tooth by Tooth Marching Algorithm

Calculation of Seal Pocket Swirl

Lab Seal Geometry Calculations

Seal with Individual Tooth Characteristics

Where,

R A D_T O O T H_{1} = R A D_T I P_{1} - {\frac{H T_{1}}{2}}_{}

R A D_T O O T H_{2} = R A D_T I P_{2} - \frac{H T_{2}}{2}

C L_{a v g} = \frac{C L_T O O T H_{1} + C L_T O O T H_{2}}{2}

Use the following to calculate the seal “rotor” surface area:

α_{1} = \frac{A N_{1}}{2} + S L_{1}

α_{2} = \frac{A N_{2}}{2} - S L_{2}

y_{1} = \frac{H T}{cos (α_{1})}

y_{2} = \frac{H T}{cos (α_{2})}

x = P T_{p k t} - W T_{2} - H T_{1} * \tan (α_{1}) - H T_{2} * tan (α_{2})

Surface area per pocket:

Surface area for all pockets:

A_{r s_t o t a l} = \sum_{1}^{n u m p k t} A_{r s}

The labyrinth seal “stator” surface area is calculated using the following:

P_{s t a t_p k t} = P T

Surface area per pocket:

A_{s s} = 2 * π * R a d_{s t a t} * P_{s t a t_p k t}

Where,

R a d_{s t a t} = (\frac{R A D_T O O T H_{1} + R A D_T O O T H_{2}}{2}) + C L_{a v g}

Surface area for all pockets:

A_{s s_t o t a l} = {\sum_{1}^{n u m p k t} A_{s s}}_{}^{}

Sultanian Friction (ref 9)

Rotor Surface:

F_{R} = \frac{0.070 * {|β|}^{0.65}}{R e^{0.2} * {|β - X K|}^{0.65}}

Stator Surface:

F_{S} = \frac{0.063}{R e^{0.2} * {|X K|}^{0.13}}

Calculation of Seal Windage Temperature Rise

Seal Pocket Heat Transfer

In addition to the fluid temperature change due to windage, the fluid temperature can also change due to the fluid convection to the pocket surface. The convection Q is applied at each pocket. The typical convection heat transfer equation is used:

q_{c o n v e c t i o n} = H T C * A r e a * (T_{s u r f} - T_{f l u i d r e l})

HTC = heat transfer coefficient that is user-defined or calculated by the correlation.

Area = pocket surface area.

T_surf = the surface temperature (user-defined).

T_{fluid rel} = the relative fluid total temperature, adjusted for fluid and surface rotation.

Labyrinth Seal TbT Element Output

Output is saved to the *.res file. Use the Output Control panel to control the output units.


Name	Description	Units ENG,SI
SEAL_POSITIVE_FLOW_DIRECTION	The positive flow direction through the seal. 1: Axial direction for the positive flow is assumed to be the direction defined by THETA = 0, PHI = 0. -1: Axial direction for positive flow is assumed to be the direction defined by THETA = 180, PHI = 0.
PRESSURE	Static pressure in every pocket in the seal is output in the form of a table in a *.res file.	Psi, MPa
TEMPERATURE	Total temperature in every pocket in the seal is output in the form of a table in a *.resfile.	⁰F, K
RHO	Density in every pocket in the seal is output in the form of a table in a *.res file.	lbm/ft³, kg/m³
TOOTH	Seal tooth type (STRAIGHT or SLANT).	None
CL	Seal clearance for every tooth is provided in the form of a table in a *.res file.	Inch,mm
AREA	Seal geometric flow area for every tooth is provided in the form of a table in a *.res file.	Inch², mm²
RAD	Nominal seal radius. Distance from engine centerline to the seal tooth tip.	Inch,m
WT	Axial width of seal tooth tip.	Inch,mm
PT	Seal axial pitch.	Inch,mm
NO_TEETH	Number of seal teeth.	(number)
HT	Seal tooth height. This variable influences only the windage calculated for a rotating seal.	Inch,mm
TYPE	Pocket type, either STRAIGHT or STEPPED as identified by the solver.	-
K/E_RPM	Rotational speed of the rotor surface.	rev/min
LAND_RPM	Rotational speed of the land surface. Also referred to as “stator”.	rev/min
DT	Absolute total temperature rise across the seal.	degF,k
TEX	Absolute total temperature at the exit of the seal.	degF,k
XKABS_IN	Swirl ratio entering the seal. Swirl in the absolute frame of reference.	None
XKABS_OUT	Swirl ratio exiting the seal. Swirl in the absolute frame of reference.	None
ASR_TOTAL	Rotor surface area.	In^2,m^2
ASS_TOTAL	Stator(aka Land) surface area.	In^2,m^2
DH_POCKET	Hydraulic diameter of the seal pockets. Assume each pocket is same.	Inch,mm
KFAC	Calculated clearance factor.	None
KEMULT	Calculated kinetic energy carryover factor.	None
HCMULT	Calculated Honeycomb Flow knockdown factor.	None
SLMULT	Calculated slanted tooth flow knockdown factor.	None


Name	Description	Units ENG,SI
Expansion Factor	Expansion factor across every tooth for compressible flows.	-
XKrel	Swirl ratio in each pocket. Swirl relative to the land, which is usually stationary. If the land is stationary XKrel is in the absolute frame of reference.	None
WIND.	Windage in each pocket.	BTU/s,W
ReynR	Reynolds number relative to the rotor surface.	None
FricFannR	Fanning Friction factor on the rotor surface.	None
ReynS	Reynolds number relative to the stator surface.	None
FricFannS	Fanning Friction factor on the stator surface.	None
MACH NO.	The Mach number of the flow in every tooth gap. Based on physical area times HCMULT if greater than 1.0.	None
Re	Reynolds number of the flow in the tooth gap.	None

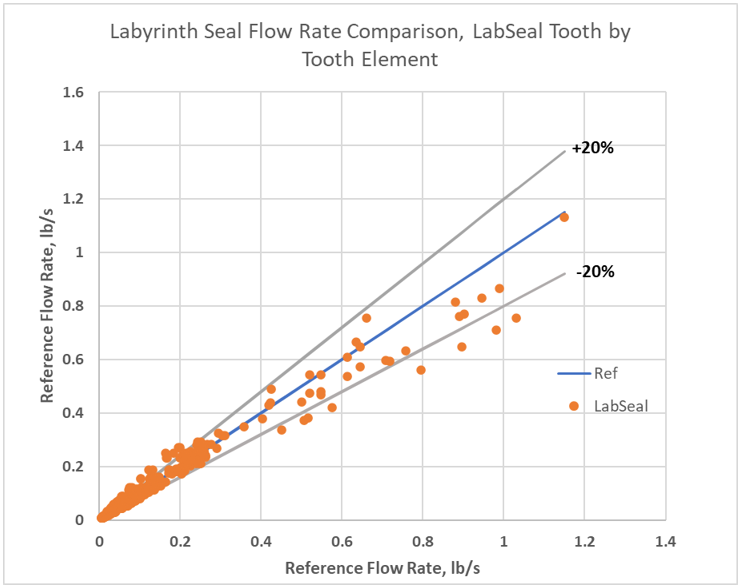
Labyrinth Seal TbT Validation

The labyrinth seal tooth by tooth results were compared to results from Tipton et al. (ref 7).

There are 705 labyrinth seal cases with a wide range of geometries and operating conditions.

Geometries

Number of teeth: 1, 3, 4, 5, 6, 10, 18

Step Height(in): -0.12, 0, +0.12

Honeycomb (in): Solid, 1/32, 1/16, 1/8

Tooth Slant Angle (deg): 0, 20, 40, 42.5

Tooth Wedge Angle (deg): 0, 10, 14, 15, 19

Tooth Spacing (in): 0.1, 0.177, 0.179, 0.25, 0.30, 0.354, 0.378, 0.626

Tooth Height (in): 0.1, 0.126, 0.135, 0.17, 0.25, 0.5

Tooth Tip Radius (in): 2.0, 2.26, 3.0, 3.36, 5.0, 7.63

Clearance (in): 0.004, to 0.061

Geometry Ratios

Pitch/Clearance: 4 to 156

Width/Clearance: 0.25 to 62.75

Width/Pitch: 0.031 to 0.67

Width/Honeycomb Size: 0.08 to 0.48

Clearance/Honeycomb Size: 0.04 to 0.65

Operating Conditions

Pressure Ratio: 1.04 to 6.8

Rotor Speed (RPM): 0, 13000, 20000, 30000

Element Leakage Flow Factor Settings

Statistics of the comparison based on:

% E r r o r = \frac{F S F l o w - T e s t F l o w}{T e s t F l o w} * 100


Avg	Mean	Max	Min	Std_dev	Count	Within +/10%	Within +/20%
10%	6%	59%	-30%	14%	705	459	632

459 out of 705 test cases match within 10%.

Labyrinth Seal Tooth by Tooth References

Vermes, Geza, “A Fluid Mechanics Approach to the Labyrinth Seal Leakage Problem,” Transactions of the ASME, Journal of Engineering for Power, April 1961, pp161-169.
Suryanarayanan, S & Morrison G.L “Labyrinth Seal Discharge Coefficient for Rectangular Cavities”, ASME 2009.
K.J. Bell & O.P. Bergelin, "Flow Through Annular Orifices", ASME 1957.
Schramm V., Willenborg K., Kim S., Wittig S., “Influence of a Honeycomb Facing on the Flow Through a Stepped Labyrinth Seal” ASME 2002.
Stocker,H. L., 1978, ‘‘Determining and Improving Labyrinth Seal Performance in Current and Advanced High Performance Gas Turbines,’’ AGARD CP273.
McGreehan W.F., & Ko S.H.,1989, “Power Dissipation in Smooth and Honeycomb Labyrinth Seals” ASME Paper No 89-FT-220.
Tipton D.L., Scott T.E, Vogel R.E., 1986, “Labyrinth Seal Analysis. Volume 3. Analytical and Experimental Development of a Design Model for Labyrinth Seals” AFWAL-TR-85-2103.
Zimmermann H., Wolff K. H., “Air System Correlations Part 1: Labyrinth Seals” ASME 98-GT-206.
Bijay K. Sultanian, “Gas Turbines – Internal Flow Systems Modeling”, Cambridge Aerospace series, 2018, ISBN 978-1-107-17009-4.
Eldin, A. M. G., “Leakage and Rotordynamic Effects of Pocket Damper Seals and See-Through Labyrinth Seals”, Texas A&M Dissertation, 2007.