材料破断の可能性の解析

破断基準

さまざまな破断基準を迅速に計算し、結果を動的に更新します。材料破断の条件は、以下の不等式で表現できます。

基準値<1

この不等式が成立していれば材料は安全です。基準値は、指定された位置における材料の応力の状態に依存します。安全率は基準値の逆数です。この不等式の両辺を基準値で除算すると、安全率で表現した破断条件が得られます。

安全率=1/基準値

Note: 適切な破断基準は材料と用途によって異なります。また、個々の設計に適切と見なされる安全の度合いも反映されます。SimSolidでは材料ごとにデフォルトの基準が用意されていますが、それらはあくまでも例にすぎません。どの基準を使用するかは、最終的に設計担当部門で判断する必要があります。

SimSolidの安全領域コンター

安全領域のコンターは、3色（赤、黄、緑）のバンドで表されます。バンド間のしきい値は、Safety Factor LowとSafety Factor Highで制御します。これらの係数は基準値の乗数として機能し、受け入れ可能と想定している不確実性の程度を反映しています。例えば、安全率の値が1.25であれば、破断基準の値に25%の安全限界があることを示しています。

破断の理論

破断の理論は材料に固有であり、その形成は検討対象としている材料のタイプに依存します。

延性材料: 延性材料では、降伏によって破断が発生します。ほとんどの金属と一部のプラスチックが延性材料に属します。材料の引張降伏強度（TYS）を使用して使用応力を判断します。降伏に至るまで、材料の応答は弾性であることを前提とします。

Figure 1.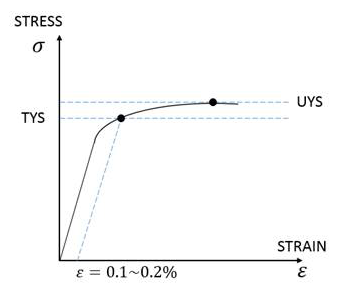
多くの鋼、特に熱処理した材料には明確な弾性限界がありません。この場合は、塑性ひずみがおよそ0.1～0.2%になるポイントを降伏強度とすることが普通です。
CAUTION:
多くの場合、鋼は延性材料と考えられますが、例外となる場合もあります。-7～+5°C程度の低温環境では、多くの鋼が延性特性を失い始めます。温度が遷移温度を下回ると、鋼を延性材料として扱うことはできなくなります。

材料の破断を判断するためのベストプラクティスについては、材料の供給元に問い合わせることをお勧めします。
脆性材料: 脆性材料では、破壊によって破断が発生するので、破断の基準が延性材料とは異なります。圧縮での破壊応力は、引張での破壊応力よりもはるかに大きい値になります。

Figure 2.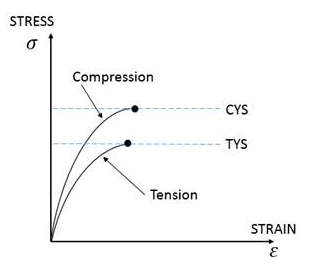

SimSolidに用意されている破断理論は次のとおりです：

フォンミーゼス応力（最大値）: この理論は、延性材料に最適で、最大変形エネルギー基準、八面体せん断応力理論、Maxwell-Huber-Hencky-von Mises理論とも呼ばれます。この値は、フォンミーゼズ応力に対する材料の引張降伏強度の比率として計算します。通常は、実験結果と最も良好に一致すると見なされています。
最大せん断応力: この理論は延性材料に最適で、Trescaの基準またはGuestの基準とも呼ばれます。この理論では、モデルの最大せん断応力が、引張試験で降伏が始まった試験体の最大せん断応力に等しくなると、モデルの降伏が始まるとしています。フォンミーゼズ応力（最大値）の理論と比較すると、最大せん断応力は控え目な手法です。この理論では応力が15%過大に見積もられることがあります。
最大法線応力: この理論は脆性材料に最適で、クーロンの基準とも呼ばれます。最大主応力に対する材料の引張強度と圧縮強度の比率を考察することによって計算します。
クリステンセン破断基準: 延性材料の破断基準と脆性材料の破断基準との乖離を埋めることを目的として最近提案された理論です。クリステンセン破断基準は、競合する破断メカニズムを表す2つの独立した下位基準で構成されています。一方の下位基準は、フォンミーゼズ基準と類似しており、もう一方の下位基準は、モール-クーロン破断基準に類似した座標の破壊基準です。

破断基準の公式

Table 1.
基準	公式
フォンミーゼス応力（最大値）	$SF = \frac{σ_{tensile yield}}{σ_{von Mises}}$
最大せん断応力	$SF = \frac{σ_{tensile yield}}{2 τ_{\max}}$ 各値の意味は次のとおりです： $τ_{max} = maximum (\|\frac{σ_{1} - σ_{2}}{2}\|, \|\frac{σ_{2} - σ_{3}}{2}\|, \|\frac{σ_{3} - σ_{1}}{2}\|)$
最大法線応力	${SF}_{i} = \frac{σ_{tensile yield}}{σ_{i}}$ $σ_{i}$ > 0の場合、かつ ${SF}_{i} = \frac{σ_{compressive yield}}{σ_{i}}$ $σ_{i}$ < 0 の場合（i = 1、2、3） $SF = minimum ({SF}_{1}, {SF}_{2}, {SF}_{3})$
クリステンセン破断基準	$(\frac{σ_{tensile}}{σ_{compressive}} \leq \frac{1}{2})$ の場合 ${SF}_{1} = \frac{σ_{tensile}}{σ_{1}}, {SF}_{2} = \frac{σ_{tensile}}{σ_{2}}, {SF}_{3} = \frac{σ_{tensile}}{σ_{3}}$ ${SF}_{4} = \frac{1}{\sqrt{E Q}}$ $SF = minimum ({SF}_{1}, {SF}_{2}, {SF}_{3}, {SF}_{4})$ 各値の意味は次のとおりです： $EQ = (\frac{1}{σ_{tensile}} - \frac{1}{σ_{compressive}}) (σ_{1} {+σ}_{2} {+σ}_{3}) + (\frac{1}{σ_{yield} σ_{compressive}}) (σ_{von Mises}^{2})$