B(H) law: Linear analytical soft magnetic material
Presentation
This model defines a linear analytical B(H) dependence without taking into consideration the saturation phenomenon for an isotropic material. It can be utilized for fields of low values, as long as the saturation knee is not reached.
Mathematical model
This model is a straight line.
The corresponding mathematical formula is written as follows:
Β(Η)=μ0μrΗ
where:
- μ0 is the permeability of vacuum, μ0 = 4 π 10-7 H/m
- μr is the relative permeability of the material
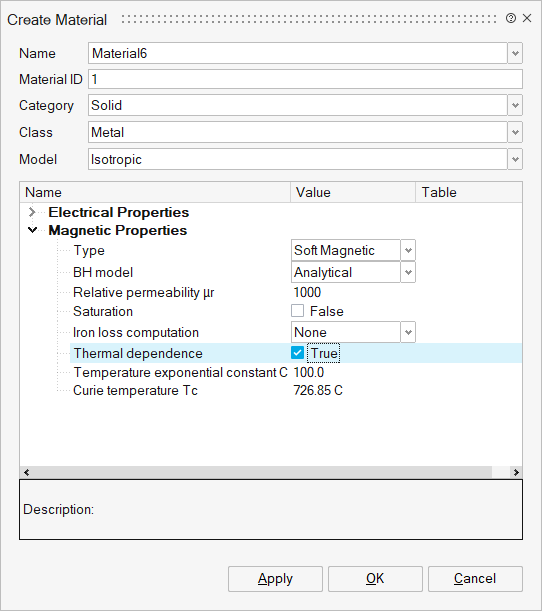
The shape of the B(H) dependence is given in the figure below.
Mathematical model dependent on temperature
This model is based on a straight line equation whose μr slope varies with the temperature.
The corresponding mathematical formula is written:
Β(Η,T)=μ0Η + μ0.(μr0-1) . coeff (T) . H
where:
- μ0 is the permeability of vacuum; μ0 = 4 π 10-7 H/m
- μr0 is the relative permeability of the material for T = 0 °C
- coeff(T) is the temperature coefficient function which describes how the magnetic susceptibility χ decreases when the temperature increases
The shape of the B(H) curve for several temperature values is presented in the figure below.
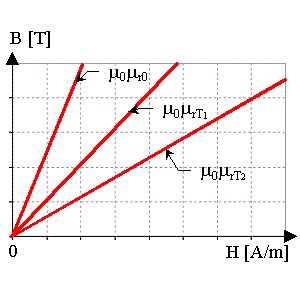
Dialog box
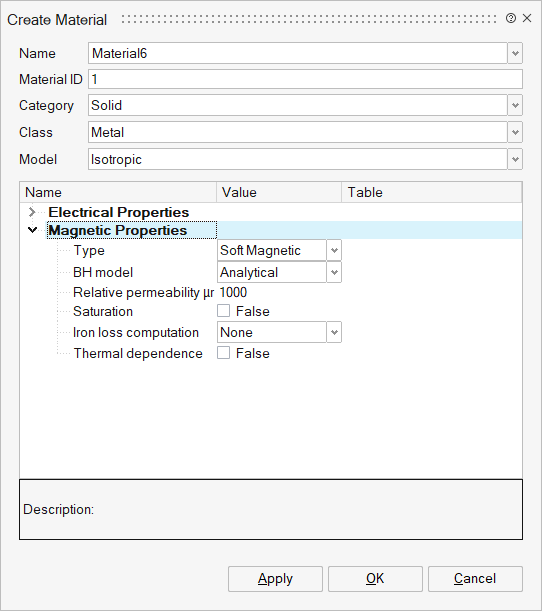
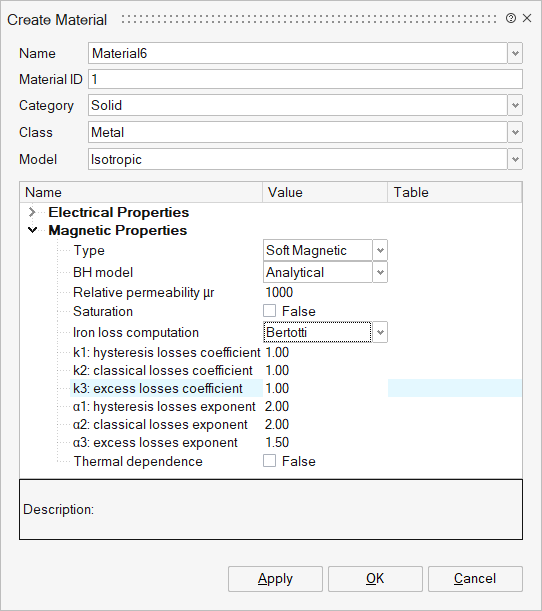
| Without Iron Loss Computation | With Iron Loss Computation |
|---|---|
 |
 |
- Open a Create Material dialog box in menu
- Choose Solid as Category field
- Choose Metal as Class field
- In Magnetic Properties:
- Choose Soft Magnetic type
- Choose Analytical BH model
- Define Relative permeabilityNote: The option of saturation allows to have a non linear analytical soft magnetic model. See this following page for the details of this model:B(H) law: Nonlinear analytical Soft magnetic material
- In Iron loss computation
- choose None to don't take into
account Iron Loss computation
or
- Choose Bertotti and define coefficients and exponents of Bertotti Model
Note: More details about Iron Losses and Bertotti Model - choose None to don't take into
account Iron Loss computation
- Activate Thermal dependence and define
corresponding parameters (optional)
- Define Temperature exponential constant C
- Define Curie temperature Tc
-