インプリシット形状のスムージング
インプリシットモデリングで作成されたオブジェクトのノイズ除去に使用します。インプリシットボディにある不要なフィーチャー(微小または鋭角なフィーチャー)を小さくしたり削除したりします。
-
インプリシットモデリングリボンで、スムーズツールを選択します。

ヒント: ツールを検索して開くには、Ctrl+Fキーを押します。詳細については、ツールの検出と検索を参照してください。 - オプション: 表示品質では、低いから非常に高いの中から選択します。要素密度の低いものから非常に高いものまで対応します。品質が高いほどより鮮明に形状フィーチャーが生成されますが、処理速度は遅くなります。複雑な関数を作成する場合は、低い品質で作業し、関数が完成した後に高い品質に切り替えることをお勧めします。
- スムージングするインプリシットボディを選択します。
-
選択した形状のスムージングに使用するアルゴリズムのタイプを選択します。
- Mean:各位置のスカラー値は、フィールド内のその位置を中心とするカーネル内のすべての値の平均値に置き換えられます。この手法は平面領域でよく機能します。しかし、鋭いエッジではフィレットのような効果があり、カーブしたサーフェスでは以前はモデルになかった継ぎ目やその他のノイズが混入することがあります。過度なMeanスムージングはモデルの体積を減少させ、時には薄いフィーチャーや小さなフィーチャーを破壊することがあるためご注意ください。
- Median:各位置のスカラー値は、フィールド内のその位置を中心とするカーネル内のすべてのスカラー値の中央値に置き換えられる。このスムージングタイプは、フィールドでの鋭く突発的な乱れである「ソルトアンドペッパー」や「インパルス」ノイズの除去に特に適しています。この手法は平面領域でうまく機能する傾向があります。しかし、鋭角エッジでは面取りのような効果があり、カーブしたサーフェスでは以前はモデルになかった小さな継ぎ目が生じることがあります。Medianフィルターは、非線形のランクフィルターで、ウィンドウ内の中央値を計算するためにカーネル内のスカラー値を並べ替える必要があるため、計算に比較的時間がかかります。
- Gaussian:Mean方式に似ていますが、ウィンドウ(カーネル)内の隣接する値には、カーネルの中心にあるスカラー値とは異なる(より低い)重み付けが与えられ、Gaussian分布を使って割り当てられます。計算速度の遅い真のGaussian分布を使用するのではなく、(Gaussianスムージングの反復ごとに)平均フィルタの連続した5回の反復を適用することでガウス分布を正確に近似し、真のGaussianスムージングの結果に非常に近い近似を実現します。この方法は、局所化とノイズ除去の間で良いトレードオフを提供します。しかし、「ソルトアンドペッパー」や「インパルス」ノイズは、Medianアプローチほどうまく処理できません。過度なGaussianスムージングはモデルの体積を減少させ、時には薄いフィーチャーや小さなフィーチャーを破壊することがあるためご注意ください。
- Laplacian:この方法は、7点離Discrete Laplacianカーネルを使用してスカラーフィールドをスムージングします。これはスムージングオペレーションの中で最も穏やかなもので、各反復でモデルの体積をわずかに減少させるだけです。他のフィルタとは異なり、Laplacianスムージングは、モデルから大きなアーティファクトを除去するために、さらに多くの反復処理が必要です。
- 幅を定義します。これはスムージングカーネルの大きさです。
- 繰り返し数を定義します。これはスムージングカーネルが実行される回数です。
- 強さを定義し、スムージング結果を0%(全くスムージングしない)から100%(幅と繰り返し数の設定に従った全強度スムージング)の間でモーフィングします。強さは、この機能を持つような繊細なアプリケーションで、スムージングの厳しさを軽減するために使用されるべきです。インプリシット形状のモーフィングを参照することで、さらなる洞察を得ることができます。
- OKをクリックします。
-
異なるスムージング技術がインプリシットモデリングの形状にどのような影響を与えるかを視覚的に示すために、以下の画像は異なるスムージングカーネルと異なる設定を使用して作成されています。各画像には、それぞれのケースにおける主な観察の概要を示す解説があります。
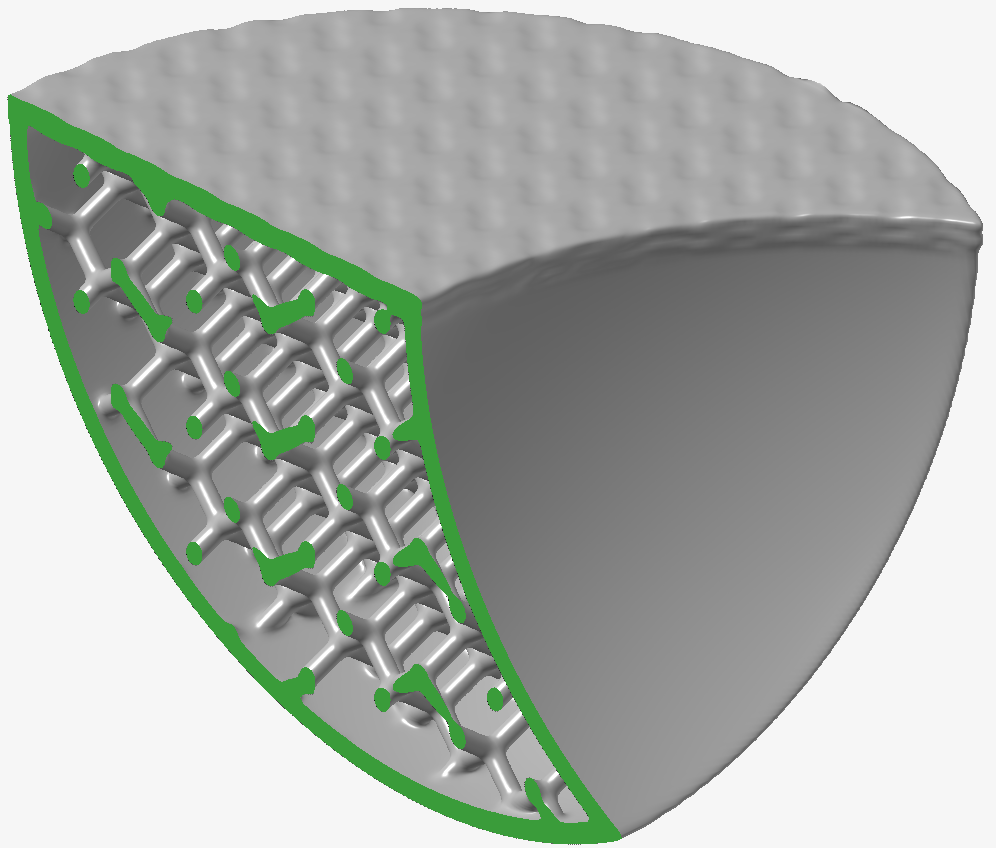
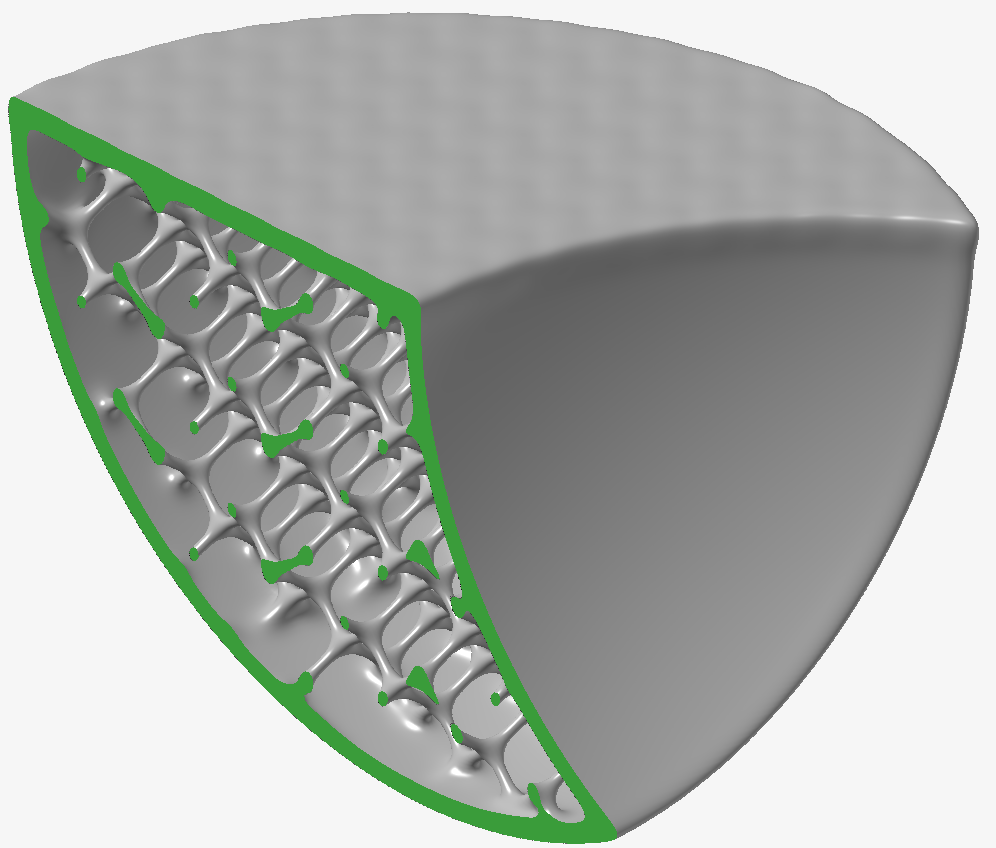
異なるスムージングフィルタの長所と短所を強調するために、以下のテストモデルを作成しました。このモデルは、球面、平面、細かいディテールを持つ埋め込みラティス、そして上面に意図的に粗くデザインされたテクスチャで構成されており、ノイズの多いアーチファクトが残っています。いくつかのブール演算の結果、曲率の高い部分(やや鋭いエッジとコーナー)もモデル内に存在します。緑色の部分は、断面を使用してオブジェクト内部のラティスを露出させたものです。
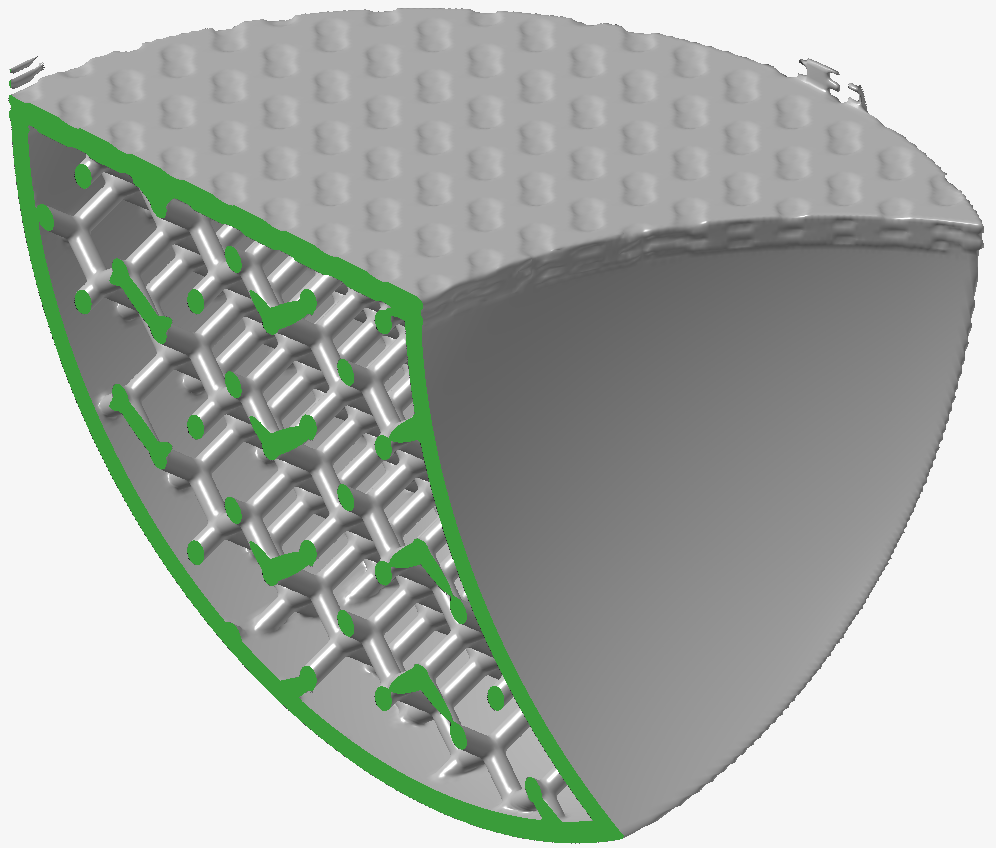
Meanスムージング
幅1(3x3x3ボクセルカーネル)と1回の反復を使用しています。- 上面のノイズアーティファクトが削除されました。
- テクスチャの深さとディテールの両方が減少しています。
- よりシャープな球状のエッジに沿ったノイズが望ましい形で減少しています。
- シャープなまま維持したかった球状のエッジが、顕著に丸くなりました。
- ラティスストラットはわずかに細くなり、ノードと外殻との接合部にはフィレットのような顕著な接合部があり、これは応力上昇を緩和するのに非常に便利です。
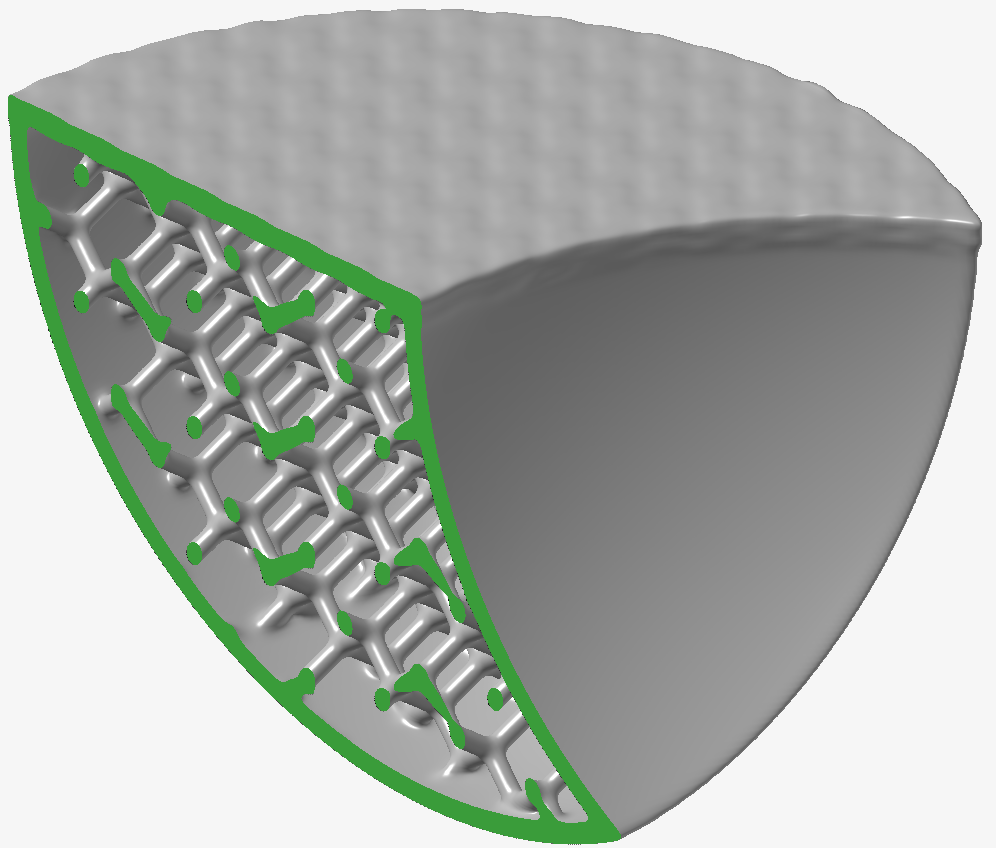

興味深いことに、カーネルの幅を2に増やし(5 x 5 x 5ボクセルカーネル)、繰り返し数1を使用すると、繰り返し数2で同じカーネルを使用した前の例よりも深刻です。下の画像では、ラティスのストラットはさらに細くなり、テクスチャはほぼ完全に失われています。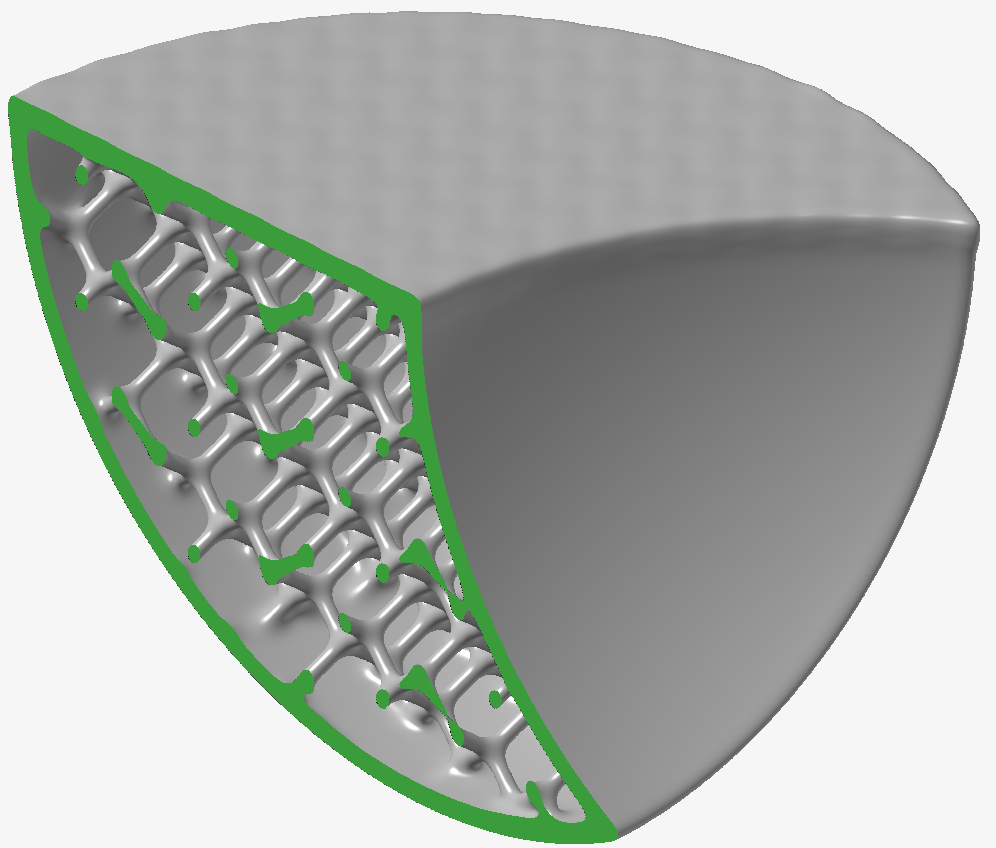
最後に、幅2と繰り返し数2を使用すると、Meanスムージングはラティス内のストラットを破壊し始め、テクスチャは実質的に消失します。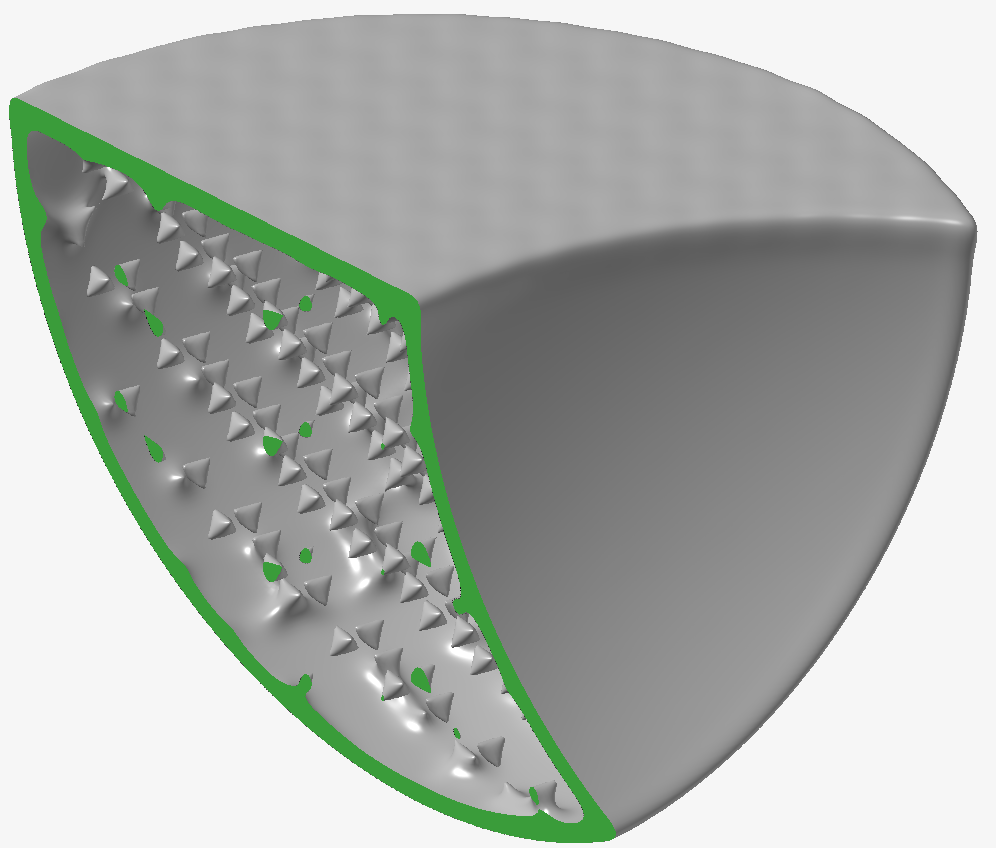
Medianスムージング
Medianスムージングは数学的、 計算上の構成が他のフィルターとかなり異なります。カーネル内の値に順位をつけてから中間の値を選ぶ唯一のフィルターです。したがって本質的に非線形です。カーネル幅1、繰り返し数1で以下の結果が得られます。
- 上面のノイズアーティファクトが削除されました。
- テクスチャの深さとディテールの両方が保持されています(Meanスムージングよりも)。
- よりシャープな球状のエッジに沿ったノイズが望ましい形で減少しています。
- シャープなまま維持したかった球状のエッジは、Meanスムージングよりもシャープになりました。
- ラティスストラットはわずかに細くなり、ノードと外殻との接合部にはフィレットのような顕著な接合部があり、これは応力上昇を緩和するのに非常に便利です。
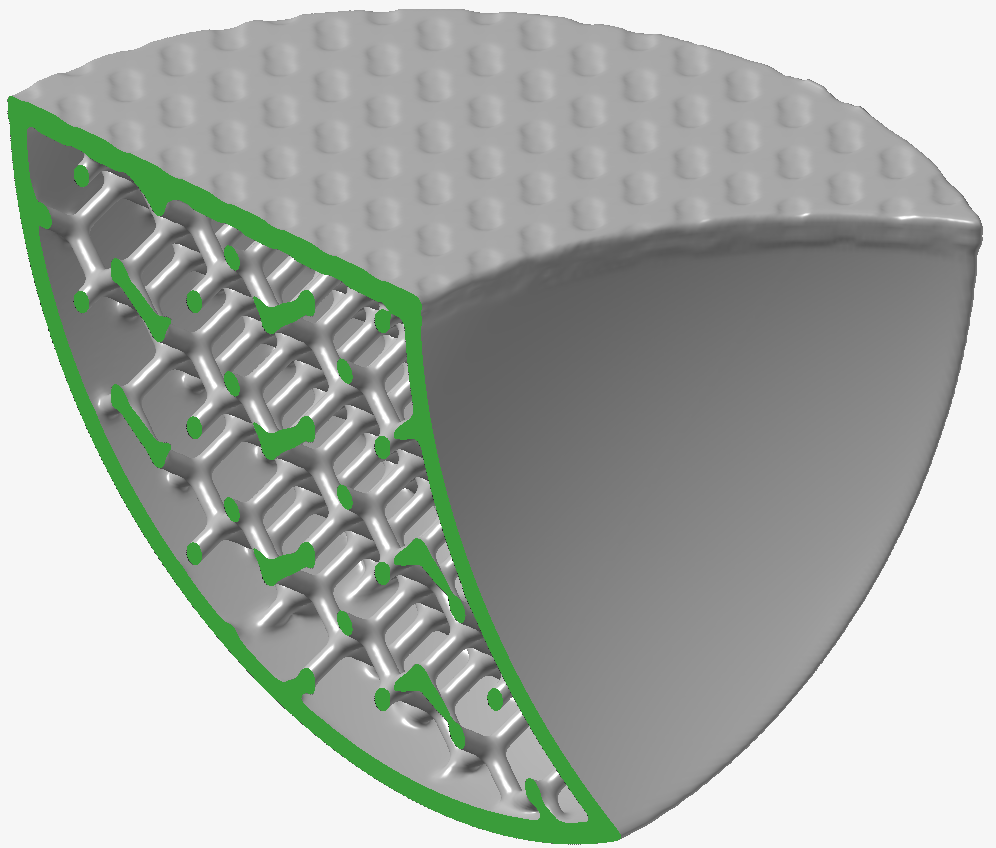
繰り返し数を多くして幅を小さくすることは、繰り返し数を少なくして幅を大きくすることよりも、一般に深刻度が低いことを示すだけで十分です。より深刻な影響を示すために、次の画像は幅を2、繰り返し数を2として作成したものです。主要な観察結果は次のとおりです。- テクスチャはまだはっきりと見えます。
- ラティスのノードは丸くなりましたが、ラティスのストラット幅は著しく減少しています。ただし、Meanスムージングで同じ設定を使用した場合とは異なり、ストラットの多くはまだ見えています。
- シャープなエッジのいくつかは丸みを帯び、他のエッジは面取りのような効果を見せ始めています。
- 球面のサーフェスには、直線的な模様やテクスチャが現れ始めています。これはスムージングフィルターの非線形性の結果です。下の2番目の画像は別の視点から見たハイライトです。
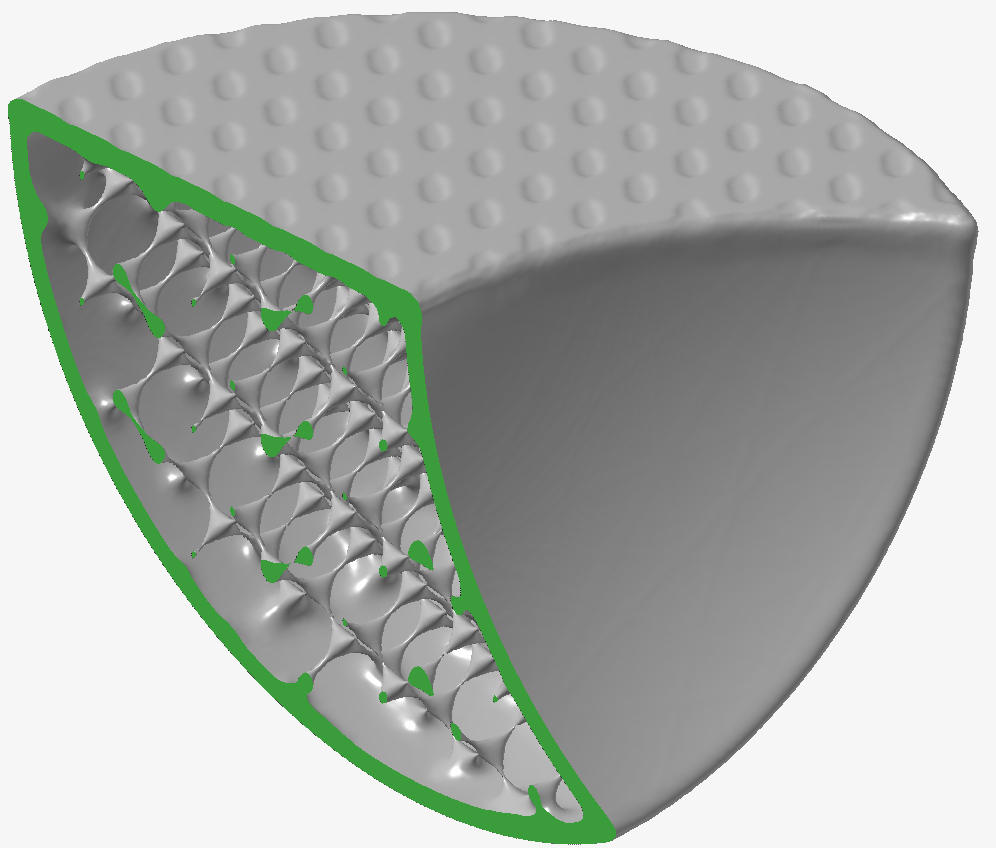

Gaussianスムージング
この実装では、Gaussianスムージングの1回の繰り返しは、Meanスムージングの5回の連続した繰り返しによって近似されます。これにより、非常に近似した結果が得られます。そのため、Gaussianスムージングの属性は、繰り返し回数の多いMeanスムージングとほぼ同じになります。ただし、予想されるように、Gaussianスムージングはやや厳しいスムージング効果をもたらし、細かいフィーチャーの厚みを減らします。以下の画像は、Gaussianスムージングを1回繰り返したもので、ノイズの多いフィーチャーの除去に成功しており、ラティスと外側のボディの間に魅力的なブレンドが作られています。しかも、テクスチャのディテールの一部が失われ、シャープなエッジが丸くなり、ラティスのストラットの幅が小さくなっています。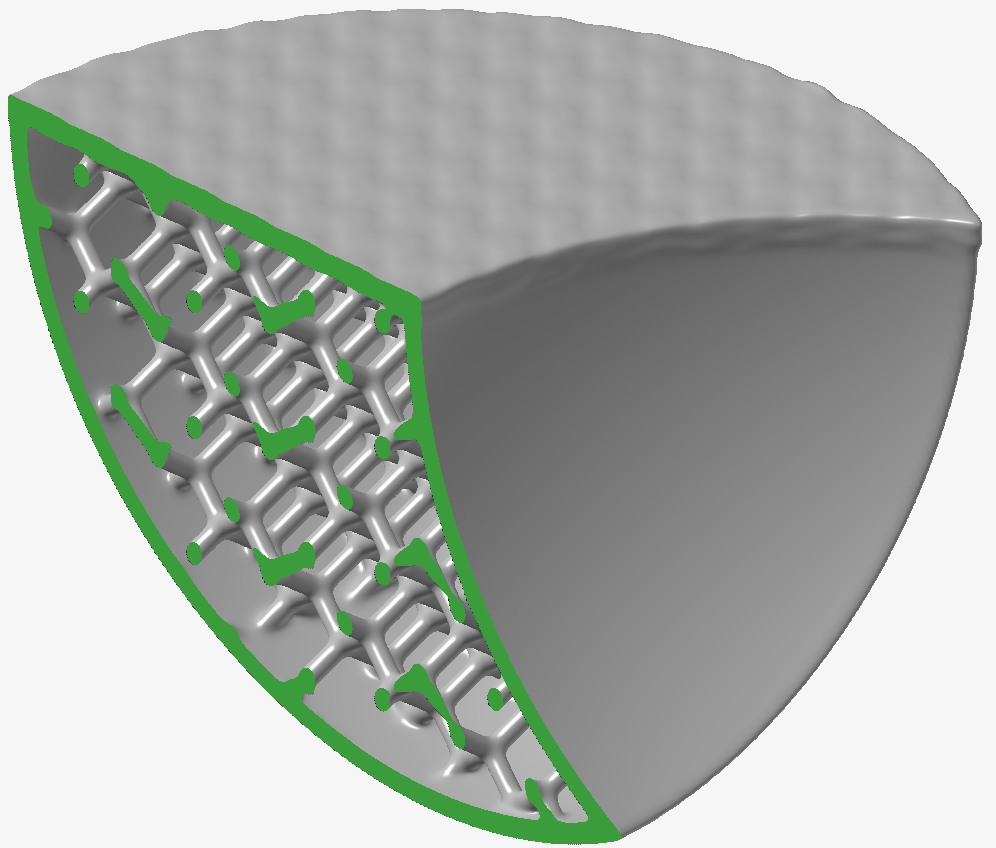
Laplacianスムージング
Laplacianスムージングは、他のスムージング手法よりも穏やかな処理を行います。そのため、大きなアーティファクトを除去するには、さらに多くの反復が必要です。Laplacianスムージングでもモデルの厚みは減少しますが、より多くの反復が必要なため、アーチファクト除去と厚み維持のバランスをより細かく制御できます。以下の2つの画像は、幅を1にして、それぞれ1回(上)と9回(下)の繰り返し数で作成したものです。これにより、スムージングと厚み減少の効果がどの程度緩やかであるかが実感できます。