RD-E: 2601 Failure Strain

Failure criteria defined in material LAW2 and LAW27.

In Radioss, one simple way to define material failure is by defining a failure strain in the material definition. In this example, a maximum plastic strain $ε_{p}^{m a x}$ is defined in LAW2 and compared to LAW27 which uses a damage model based on strain. A model with one shell element is used to understand the failure definition. In a second model a metallic thick plate is perforated by a rigid sphere.

Options and Keywords Used

Imposed velocities (/IMPVEL)
Max. plastic strain (/MAT/LAW2 (PLAS_JOHNS))
Damage model input (/MAT/LAW27 (PLAS_BRIT))
Rigid sphere (/RWALL)

Input Files

Before you begin, copy the file(s) used in this example to your working directory.

RD-E-2601_Failure_strain.zip

Model Description

A one shell element is used to demonstrate the failure model.

The material undergoes an isotropic elasto-plastic behavior which can be reproduced by a Johnson-Cook model.

Material properties are:

Properties: Value
Young's modulus: 71000 $[MPa]$
Poisson's ratio: 0.3
Density: 2.8 x 10^-3 g/mm³
Yield stress: 290 $[MPa]$
Hardening parameter: 562.3 $[MPa]$
Hardening exponent: 0.63
Maximum stress: 425

The maximum stress and the failure plastic strain are considered in the failure modeling section. The strain rate effect is not taken into account in this example. Although LAW2 and LAW27 both use a Johnson-Cook material model for elasto-plastic behavior, the failure definition included in the material law is different.

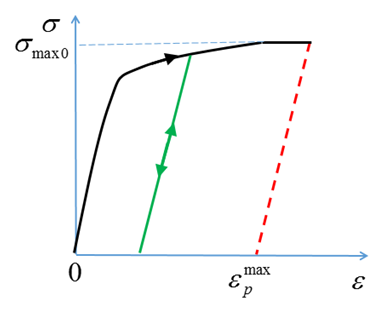
LAW2: Use Plastic Strain for Failure

In LAW2, the maximum plastic strain

ε_{p}^{m a x}

used for element failure. This means the shell element is deleted once it reaches the maximum plastic strain defined in the model. Unlike LAW27, there is no damage before failure and the failure can occur in both tension and compression.

Figure 1. Stress/Strain Curve for LAW2 with Maximum Plastic Strain

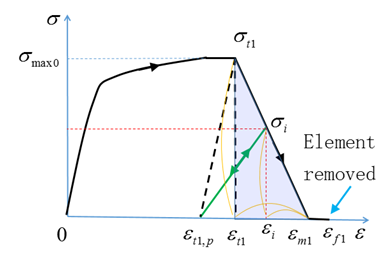
LAW27: Use a Damage Model

LAW27 is used to simulate material damage using a Johnson-Cook plasticity law. A damage model is incorporated into the material law to take into account the damage evolution where stress decreases up to element rupture. When using the material failure included in LAW27, the failure and damage occur only in tension and not compression.

The damage parameters in the principal direction $i = 1, 2$ are $ε_{t i}, ε_{f i}, ε_{m i}$ .

$ε_{t i} = 0.14$ ; $ε_{m i} = 0.15$ ; $ε_{f i} = 0.16$

When the principal strain reaches $ε_{t i} = 0.14$ , the material damage starts, based on the damage face $d_{i}$ and $d_{\max i}$ , which are given by:

d_{i} = \min (\frac{ε_{i} - ε_{t i}}{ε_{m i} - ε_{t i}}, d_{\max i})

In directions, $i = 1, 2$ .

The stress is then reduced using the damage parameter, $σ_{i}^{r e d u c e d} = σ_{i} (1 - d_{i})$ .

The damage factor in the first principal direction is a function of principal strain:

d_{i} = \min (\frac{ε_{i} - 0.14}{0.15 - 0.14}, 0.999)

Figure 2. Stress/Strain Curve for Damage Affected Material

Results

One Element Shell Model

In order to show the difference between LAW2 and LAW27, uniaxial and eqibiaxial loads are applied to a one element shell model.

Test 1: Uniaxial test
With $ε_{f 1} \begin{matrix} \end{matrix} i n \begin{matrix} \end{matrix} L A W 27 = (ε_{e} + ε_{p}^{\max}) \begin{matrix} \end{matrix} i n \begin{matrix} \end{matrix} L A W 2$
- In LAW27, $ε_{t i}, ε_{m i}, ε_{f i}$ are total strain.
- In LAW2, $ε_{p}^{m a x}$ is plastic strain.
In one shell element set:
- In LAW27, $ε_{f 1} = 0.16$
- In LAW2, $ε_{p}^{\max} = 0.1559$
So that element deleted at same strain.
$ε_{t o t a l} = ε_{e} + ε_{p} = \frac{σ_{y}}{E} + 0.1559 = \frac{290}{71000} + 0.1559 = 0.16$
Although the element is deleted at same strain the internal energy at failure is different for LAW2 and LAW27, due to the difference the failure treatment.
Figure 3. Stress versus Strain Curve . showing the failure strain in LAW2 and LAW27

Figure 4. Internal Energy Curve of the Element in LAW2 and LAW27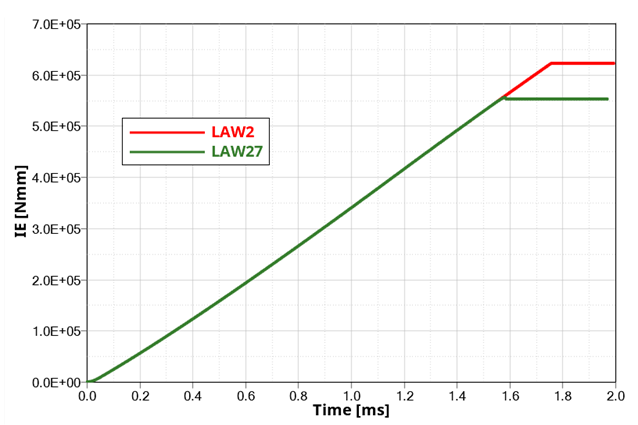
Test 2: Equibiaxial test
The failure strain values from the uniaxial test are used in a equibiaxial test.
- In LAW27, $ε_{f 1} = 0.16$
- In LAW2, $ε_{p}^{\max} = 0.1559$
Figure 5. Stress/Plastic Strain Curve for LAW2 and LAW27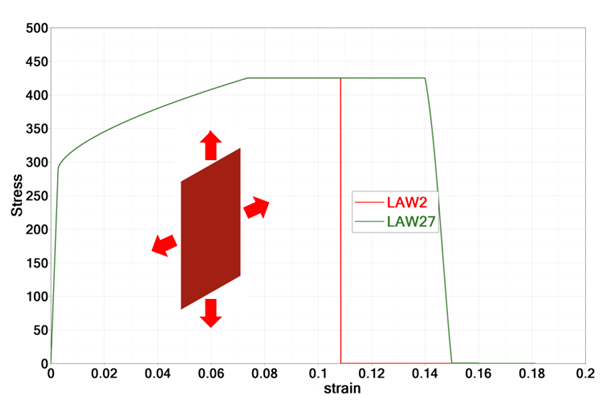
In biaxial loading, the element deletion is different for LAW2 and LAW27, due to different failure treatment in LAW2 and LAW27. In LAW2, the element is deleted when $ε_{p}^{m a x}$ is reached in the element. The change in plastic strain is:
${\dot{ε}}_{p} \cdot Δ t = \frac{σ_{V M} - σ_{y}}{E} = \frac{\sqrt{\frac{1}{2} [{(σ_{1} - σ_{2})}^{2} + σ_{1}^{2} + σ_{2}^{2}]}}{E} - \frac{σ_{y}}{E}$
For I_plas=2 radial return. For additional information, refer to Stress and Strain Calculation in the Theory Manual.

In LAW27, the element is deleted when the strain in each principal direction exceeds $ε_{f i}$ . The first principal strain in LAW27 is:

ε_{1} = \frac{σ_{1}}{(1 - d_{1}) E} - \frac{ν σ_{2}}{E}

The second principal strain is calculated in a similar manner.

Plate Impact Model

If the previous failure strains definitions in a plate example is used, the results are also different.

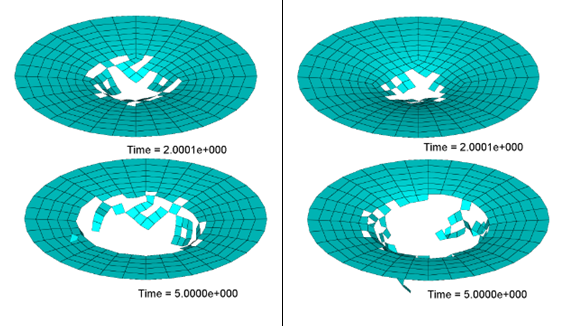
fig_26-7 — Figure 6. Failure Behavior in Plate Test. left: LAW2; right: LAW27

The previous one element biaxial tension test showed the differences in LAW2 and LAW27 in tension. Since LAW27 does not fail in compression, but LAW2 does fail in compression, this causes a difference in the plate example shown in Figure 6.

Note: The property option I_strain =1 must be defined, so that the strains are calculated and output for post-processing. This can be defined for all shell elements using /DEF_SHELL.

During the simulation, time of element failure is written to the Engine output file runname_0001.out.

For LAW2, the message is: RUPTURE OF SHELL ELEMENT NUMBER #
For LAW27, the message is: TOTAL ELEMENT TENSION FAILURE, ELEMENT #

Conclusion

Although LAW2 and LAW27 both use Johnson-Cook to describe elasto-plastic behavior, they use different failure treatment. LAW2 checks with plastic strain and LAW27 checks with principal strain. LAW27 uses damage parameter d to produce linear failure; which makes it difficult to get the same failure behavior between them.