/FAIL/TSAIHILL

Block Format Keyword Tsai-Hill failure criterion for composite materials failure modeling. This criterion is available for solids and shells.

Format

(1)	(3)	(5)	(9)	(10)
/FAIL/TSAIHILL/`mat_ID`/`unit_ID`
$X_{11}$	$X_{12}$	$S_{12}$	`I`_{fail_sh}	`I`_{fail_so}
$τ_{\max}$	`F`_cut

Optional Line:

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
`fail_ID`

Definition

Field	Contents	SI Unit Example
`mat_ID`	Material identifier. (Integer, maximum 10 digits)
`unit_ID`	(Optional) Unit identifier. (Integer, maximum 10 digits)
$X_{11}$	Longitudinal critical strength. Default = 10²⁰ (Real)	$[Pa]$
$X_{12}$	Transverse critical strength. Default = 10²⁰ (Real)	$[Pa]$
$S_{12}$	Shear critical strength. Default = 10²⁰ (Real)	$[Pa]$
`I`_{fail_sh}	Shell failure model flag. = 0 (Default) Shell is never deleted and no stress softening. = 1 Shell is deleted, if damage is reached for one layer. = 2 Shell is deleted, if damage is reached for all shell layers. (Integer)
`I`_{fail_so}	Solid failure model flag. = 0 Solid is never deleted and no stress softening. = 1 (Default) Solid is deleted, if damage is reached for one integration point of solid. = 2 Solid is deleted, if damage is reached for all integration points. (Integer)
$τ_{\max}$	Dynamic time relaxation. 5 Default = 10²⁰ (Real)	$[s]$
`F`_cut	Stress tensor filtering frequency. Default = 0.0 (Real)	$[\frac{1}{s}]$
`fail_ID`	(Optional) Failure criteria identifier. 4 (Integer, maximum 10 digits)

Example

/UNIT/1
                  Mg                  mm                   s
/FAIL/TSAIHILL/1/1
#                X11                  X22                 S12                       IFAIL_SH  IFAIL_SO 
                520.                 316.               407.5                               1         1
#            TAU_MAX                 FCUT
              1.0E-4                100.0

Comments

This failure model is available for shells and solids. It considers a composite material ply with the fibers oriented in the direction 1 (also denoted m1) and the matrix oriented in transverse direction, that is, in directions 2 (and 3 for solids). Each direction considers a critical strength value valid for both tension and compression.
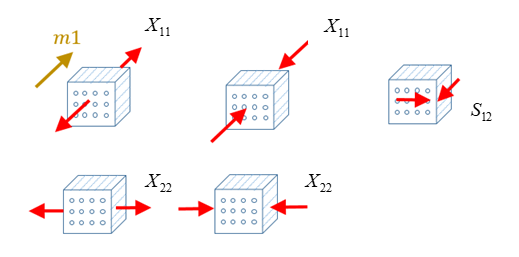Figure 1.

Where, $X_{11}$ , $X_{12}$ , $S_{12}$ are respectively the critical strength in direction 1, critical strength in direction 2 and in shear.
The failure criterion for shells is written as:(1)
$F = \frac{σ_{1}^{2}}{X_{11}^{2}} - \frac{σ_{1} σ_{2}}{X_{11}^{2}} + \frac{σ_{2}^{2}}{X_{22}^{2}} + \frac{σ_{12}^{2}}{S_{12}^{2}} \leq 1$

For solids the criterion becomes:(2)
$F = \frac{σ_{1}^{2}}{X_{11}^{2}} - \frac{σ_{1} σ_{2}}{X_{11}^{2}} - \frac{σ_{1} σ_{3}}{X_{11}^{2}} + \frac{σ_{2}^{2}}{X_{22}^{2}} + \frac{σ_{3}^{2}}{X_{22}^{2}} + \frac{σ_{12}^{2}}{S_{12}^{2}} + \frac{σ_{31}^{2}}{S_{12}^{2}} \leq 1$

The criterion is considered to be reached when $F = 1$ . In fact, the damage variable corresponds to the criterion itself $D = F$ .
Once the criterion is reached $D = F = 1$ , two behaviors can be set up:
- If I_{fail_sh} = 0 or I_{fail_so} = 0, there is no stress softening and elements are never deleted. In this case, the failure criterion is purely visual using the output of the damage variable.
- If I_{fail_sh} ≠ 0 or I_{fail_so} ≠ 0, a stress relaxation is generated to decrease the load carrying capacity of the element.(3)
  $σ (t) = f (t) \cdot σ_{d} (t_{r})$
  
  With $f (t) = \exp (- \frac{t - t_{r}}{τ_{\max}})$ and $t \geq t_{r}$ .
  
  Where,
  
  $t$
  
  Time.
  
  $t_{r}$
  
  Start time of relaxation when the damage criteria is assumed.
  
  $τ_{\max}$
  
  Time of dynamic relaxation.
  
  $σ_{d} (t_{r})$
  
  Stress tensor when the criterion is reached.
  
  When the stresses reach 1% of the stress value at the beginning of the failure, the element is deleted. This is necessary to avoid instabilities coming from a sudden deletion of an element and a failure “chain reaction” in the neighboring elements. Even if the failure criterion is reached, there will be no element deletion with the default value of $τ_{\max} = 1.0 E 20$ . Therefore, it is recommended to define a value for $τ_{\max}$ 10 times larger than the simulation time step.
To avoid “chain reaction” when deleting elements, you can also define a stress tensor filtering frequency F_cut. Thus, the stress tensor used to calculate the TSAIHILL criterion is first be filtered according to:(4)
$σ_{n + 1}^{f i l t} = α σ_{n + 1} + (1 - α) σ_{n}^{f i l t}$

With $α = \frac{2 π \cdot F_{c u t} \cdot Δ t}{2 π \cdot F_{c u t} \cdot Δ t + 1}$

Where, $Δ t$ is the current timestep.

If a filtering frequency is not defined (F_cut= 0.0), the filtering effect is deactivated.
The fail_ID is used with /STATE/BRICK/FAIL and /INIBRI/FAIL. There is no default value. If the line is blank, no value will be output for failure model variables in the /INIBRI/FAIL (written in .sta file with /STATE/BRICK/FAIL option).