/FAIL/TAB1
Block Format Keyword This advanced failure model allows the plastic failure strain to be defined as a function of: stress triaxiality, strain rate, Lode angle, element size, temperature, and instability strain. Damage is accumulated based on user-defined functions.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /FAIL/TAB1/mat_ID/unit_ID | |||||||||
| Ifail_sh | Ifail_so | P_thickfail | P_thinfail | Ixfem | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| Dcrit | Dp | n | Dadv | fct_IDd | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| table1_ID | Yscale1 | Xscale1 | table2_ID | Yscale2 | Xscale2 | ||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| fct_IDel | Fscaleel | El_ref | inst_start | Fad_exp | Ch_i_f | ||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| fct_IDT | FscaleT | Shrf | Biaxf | ||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| fail_ID |
Definition
| Field | Contents | SI Unit Example |
|---|---|---|
| mat_ID | Material
identifier. (Integer, maximum 10 digits) |
|
| unit_ID | Unit Identifier. (Integer, maximum 10 digits) |
|
| Ifail_sh | Shell failure flag. If Ixfem =0: failure - element deleted. 1 If Ixfem =1: failure - element cracked. 2 (Integer)
|
|
| Ifail_so | Solid failure flag.
(Integer) |
|
| Ixfem | XFEM flag (for
/SHELL and /SH_SANDW
properties only).
(Integer) |
|
| P_thickfail | Ratio of through thickness
integration points that must fail before the element is deleted.
(shells only). Only used when
Ifail_sh=2
or 3. 2
6
7
(Real) |
|
| P_thinfail | Ratio of thickness
reduction before failure (shells only and only active for
Ifail_sh >
1). (Real) |
|
| Dcrit | Critical accumulated
damage value (failure criteria). Default = 0.999 (Real) |
|
| Dp | Damage accumulation
parameter. Default = 1.0 (Real) |
|
| n | Damage accumulation
parameter. Default = 1.0 (Real) |
|
| Dadv | Criterion for the crack
advancement (Only active if
Ixfem=1). (Real, between 0 and 1) Default = 0 means Dadv = Dcrit 4 |
|
| fct_IDd | Damage scale factor
function identifier as function of current damage. 5 Default = 0 (Integer) |
|
| table1_ID | Failure strain table
identifier. 3 (Integer) |
|
| Yscale1 | Scale factor for the
ordinate of table1 (failure strain). Default = 1.0 (Real) |
|
| Xscale1 | Scale factor for the
abscissa table1 (strain rate). Default = 1.0 (Real) |
|
| table2_ID | Instability strain table
identifier. 9 (Integer) |
|
| Yscale2 | Scale factor for the
ordinate of table2 (instability strain). Default = 1.0 |
|
| Xscale2 | Scale factor for the
abscissa of table2 (strain rate). Default = 1.0 |
|
| fct_IDel | Element size factor
function identifier. (Integer) |
|
| Fscaleel | Element size function
scale factor. Default = 1.0 (Real) |
|
| El_ref | Reference element
size. Default = 1.0 (Real) |
|
| inst_start | Instability strain (Only
used if table2_ID is not defined). Default = Dp (Real) |
|
| Fad_exp | Fading exponent. 9
|
|
| Ch_i_f | Choice of instability or
fracture regularization flag.
|
|
| Shrf | Shear triaxiality limit
for applying element size regularization on instability
curve. Default = -1.0 (Real) |
|
| Biafx | Bi-traction triaxiality
limit for applying element size regularization on instability
curve. Default = 1.0 (Real) |
|
| fct_IDT | Temperature factor
function identifier. (Integer) |
|
| FscaleT | Temperature function scale
factor. Default = 1.0 (Real) |
|
| fail_ID | (Optional) Failure
criteria identifier. 10 (Integer, maximum 10 digits) |
Example (Shell)
#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
# MUNIT LUNIT TUNIT
kg mm ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 1. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/PLAS_JOHNS/1/1
Steel
# RHO_I
7.9E-6 0
# E Nu Iflag
210 .3 0
# a b n EPS_p_max SIG_max0
.05 .52 .1 0 0
# c EPS_DOT_0 ICC Fsmooth F_cut Chard
.022 .001 0 1 1 0
# m T_melt rhoC_p T_r
1.03 1796 3.91 300
/FAIL/TAB1/1/1
# failure for shell
# Ifail_sh Ifail_so P_THICKFAIL P_THINFAIL I_Xfem
2 1 1 0 0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
##CARD2 - Damage accumulation parameters
# DCRIT D N Dadv fct_IDd
1 .1 1 0 0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#CARD3 - Failure strain functions for each defined strain rate (Nrate lines, at least one)
#Table1_ID Yscale1 Xscale1 Table2_ID Yscale2 Xscale2
4711 1 1 4712 1 1
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#CARD4 - Element size scale function
#FCT_ID_EL FSCALE_EL EI_REF INST_START FAD_EXP Ch_i_f
21 1 1 0 10 0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#CARD5 - Temperature scale function and triaxiality limits for element size factors
# FCT_ID_T FSCALE_T Shrf Biaxf
22 1
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#CARD6 - Function identifier (optional card)
# Fail_Id
1
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 3. FUNCTIONS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/TABLE/1/4711
failure plastic-strain vs triaxiality for material failure
#
1
# Triaxiality Failure_Strain
-1. 0.50
1. 0.50
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/TABLE/1/4712
failure plastic-strain vs triaxiality for diffuse necking
#
1
# Triaxiality Failure_Strain
-1. 0.30
1. 0.30
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/21
Element length regularisation
# X Y
# relative ele. size scale factor
.1 1
.25 1
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/22
Temperature scale function
# X Y
0 1.0
1000 1.0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#enddata
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|Example (Solid)
#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
# MUNIT LUNIT TUNIT
kg mm ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 1. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/PLAS_JOHNS/1/1
Steel
# RHO_I
7.9E-6 0
# E Nu Iflag
210 .3 0
# a b n EPS_p_max SIG_max0
.05 .52 .1 0 0
# c EPS_DOT_0 ICC Fsmooth F_cut Chard
.022 .001 0 1 1 0
# m T_melt rhoC_p T_r
1.03 1796 3.91 300
/FAIL/TAB1/1/1
# Ifail_sh Ifail_so P_THICKFAIL P_THINFAIL I_Xfem
1 1 1 0 0
# DCRIT D N Dadv fct_IDd
1 1 1 0 0
#Table1_ID Yscale1 Xscale1 Table2_ID Yscale2 Xscale2
4711 1 1 0 0 0
#FCT_ID_EL FSCALE_EL EI_REF INST_START FAD_EXP Ch_i_f
21 1 1 0 0 0
# FCT_ID_T FSCALE_T Shrf Biaxf
22 1
# Fail_Id
1
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 3. FUNCTIONS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/TABLE/1/4711
curve_list Failure Function vs. strain rates vs Lode angle
#DIMENSION
3
# FCT_ID strain_rate Lode_angle
3000 1E-4 -1 0
3001 1E-4 0 0
3002 1E-4 1 0
3003 1 -1 0
3004 1 0 0
3005 1 1 0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/3000
fail strain vs triaxiality
# triaxiality fail strain
# X Y
0 .5
1 .5
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/3001
fail strain vs triaxiality
# triaxiality fail strain
# X Y
0 .5
1 .5
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/3002
fail strain vs triaxiality
# triaxiality fail strain
# X Y
0 .5
1 .5
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/3003
fail strain vs triaxiality
# triaxiality fail strain
# X Y
0 .5
1 .5
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/3004
fail strain vs triaxiality
# triaxiality fail strain
# X Y
0 .5
1 .5
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/3005
fail strain vs triaxiality
# triaxiality fail strain
# X Y
0 .5
1 .5
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/21
Element length regularisation
# X Y
# relative ele. size scale factor
0 1
10 1
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/22
Temperature scale function
# X Y
0 1
1000 1
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#enddata
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|Comments
- Using Ixfem=0, failure leads to element or layer deletion. In this case, if Ifail_sh=1, then P_thickfail has to be set to zero for proper working failure criteria.
- Using
Ixfem=1 (XFEM formulation), failure leads to
element crack:
XFEM formulation is only compatible with Belytchko (Ishell=1 or 2), Ishell=3 or 4 and QEPH (Ishell=24) shell elements.
Two XFEM options are available: mono-layer and multi-layer. The XFEM option depends on the property type associated to the failure criterion applied to the material identifier:- If /PROP/SHELL (TYPE1) is used, then mono-layer XFEM
will be applied.
In this case, the whole element thickness is considered as a single layer. The failure criterion is calculated in each integration point but only one single crack can appear in this element. This approach is compatible with all shell flag options (Ifail_sh=1, 2 or 3), as well as P_Thickfail values. The crack direction is determined by the principal constraints in the last failed integration point.
- If /PROP/SH_SANDW (TYPE11) is used, then multi-layer
XFEM will be applied.
In this case, each integration point over thickness is considered as a distinct layer. The failure criterion is calculated separately, and the crack direction may be different for each layer. Crack direction in each layer will independently propagate from one element to another. Multi-layer XFEM is not compatible with Ifail_sh=1 and P_thickfail>0. Their values will be automatically set to Ifail_sh=2 and P_thickfail=0.
Warning: Mono-layer and multi-layer XFEM formulations cannot be mixed in the same model, yet. The choice between them must be made for the whole model. - If /PROP/SHELL (TYPE1) is used, then mono-layer XFEM
will be applied.
- The plastic failure strain is defined
as:
(1) Where,- Described in table1_ID and is calculated by interpolating between the failure strain versus stress triaxiality functions for strain rate and Lode angle .
- Stress triaxiality
- Hydrostatic stress
- von Mises stress
The first function from table1_ID is used for strain rate values from 0 to its corresponding strain rate. For strain rates above the last defined function, the failure strain value is extrapolated using the last two curves and their corresponding strain rates.
It is possible to consider element size in material failure by function fct_IDel to scale the failure strain depending on the normalized element size with Ch_i_f=1 or 3.(2) Where, is the function of fct_IDel.
Element size scale factor is only applied between triaxiality limits defined by Shrf and Biaxf.(3) Outside this triaxiality range, the element size scaling is not applied to failure or instability curves.Note: If non-local regularization is used (with /NONLOCAL/MAT), the element size scaling factor is not used. If a scaling function is still defined (fct_IDel > 0), the parameters are scaled using LE_MAX parameter of the non-local card (either specified directly by you or computed from the Rlen parameter value).Temperature dependency can be considered in material failure by defining a function to scale the failure strain depending on the normalized temperature:(4) Here, is defined using fct_IDT and Temperature is computed as:(5) It is recommended to use /HEAT/MAT to define the thermal parameter for material laws (which support thermo-plasticity).
- Two different failures (rupture or crack) are
introduced in this failure model. The failure criteria is calculated
as:Element rupture (Ixfem=0):
- Element rupture (deleted), if
(6) Where, is the only rupture criterion used when Ixfem=0.
Element crack (Ixfem=1):- Element cracked, if:
(7) in case no failed neighbors for this element. is used for new crack initialization.(8) in case there is failed neighbors for this element, is used for crack advancement.
Element is deleted, if a second crack arrives to the same element.
Note: should always be less than ( < ). If not, then is set to crit ( = ). - Element rupture (deleted), if
- Damage accumulation is computed in Radioss one of two different ways:
- With parameter input, if
fct_IDd =
0:
(9) Where,- Change in plastic strain of the integration point.
- Plastic failure strain.
- Dp and n
- Damage parameters.
- With curve input, if
fct_IDd ≠
0:
(10) Where, is the damage scale factor as a function of current damage defined in fct_IDd.
- With parameter input, if
fct_IDd =
0:
- P_thickfail is only compatible with shell elements (except, shells with /PROP/TYPE11 (SH_SANDW)) and is only used when Ifail_sh=2 or Ifail_sh=3. If Ixfem=1, P_thickfail is only compatible with mono-layer XFEM formulation. 1
- When
P_thickfail is used,
the shell complete rupture occurs when the thickness of broken layers is greater
than the ratio of shell total thickness. Any P_thickfail
value defined in the shell properties is ignored and the value entered in this
failure model is used instead.
Only adjacent layers that fail consecutively are accounted for the thickness sum (usually from one of external skin to the mid-surface).
- The first variable of
table1_ID is the plastic failure strain versus stress
triaxiality function, the second variable is strain rate and the third is the
Lode angle parameter
(for solids).
For shell, only 2D tables are available (no dependency of Lode angle).
- Instability (diffuse necking):
- Only available for shells
- The fading exponent describes the softening behvior and starts of
instability (diffuse necking). The recommended value of
Fad_exp is 5 to 10.
If Fad_exp < 0 and Ch_i_f=2 or 3, then the absolute value of the fading exponent is a function identifier fct_IDel which defines the fading exponent as a function of element length.
- The start of instability can be described as a function or constant
value:
- table2_ID is a function of instability strain
versus triaxiality where the instability strain defines when
diffuse necking starts. Strain rate dependency for diffuse
necking could be considered as well using
dimension=2 in
/TABLE.
(11) - If table2_ID is not defined,
inst_start is used as constant flat line
for instability starting value over the triaxiality, where the
default value is
Dp.
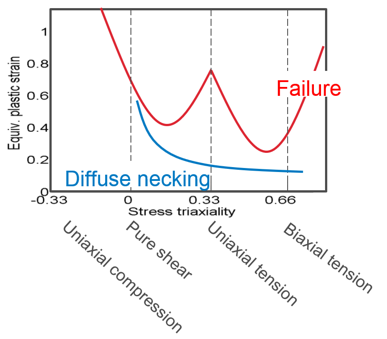
Figure 1.
- table2_ID is a function of instability strain
versus triaxiality where the instability strain defines when
diffuse necking starts. Strain rate dependency for diffuse
necking could be considered as well using
dimension=2 in
/TABLE.
- The diffuse necking softening is based according to this
equation:
(12) Where, with being the diffuse necking strain.
Currently, diffuse necking (material instability) in /FAIL/TAB1 could be used with material laws greater than 28.
- The fail_ID is used with /STATE/BRICK/FAIL and /INIBRI/FAIL. There is no default value. If the line is blank, no value will be output for failure model variables in the /INIBRI/FAIL (written in the .sta file with /STATE/BRICK/FAIL option).