/FAIL/ORTHBIQUAD
Block Format Keyword This failure model uses an orthotropic simplified nonlinear, plastic strain-based, failure criteria with linear damage accumulation.
For several loading directions, the failure strain is described by two parabolic functions calculated using curve fitting from up to 5 user input failure strains. For all loading directions that are not given in the input, an interpolation of the failure strain evolution with stress triaxiality will be done during the simulation. You can give up to 10 different set of parameters for 10 different directions equally distributed between 1st material direction (0 degree) and 2nd material direction (90 degrees).
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /FAIL/ORTHBIQUAD/mat_ID/unit_ID | |||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| P_thickfail | M-Flag | S-Flag | Nangle | fct_IDel | El_ref | ||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| c5 | CJC | fct_IDrate | Rate_Scale | ||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| r1 | r2 | r4 | r5 | ||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| c1 | c2 | c3 | c4 | Inst_start | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| fail_ID |
Definition
| Field | Contents | SI Unit Example |
|---|---|---|
| mat_ID | Material identifier. (Integer, maximum 10 digits) |
|
| unit_ID | (Optional) Unit identifier. (Integer, maximum 10 digits) |
|
| P_thickfail | Ratio of through thickness
integration points that must fail before the element is deleted.
(shells only). Default = 1.0 (Real) |
|
| M-Flag | Material selector flag.
(Integer) |
|
| S-Flag | Specific behavior flag.
|
|
| Nangle | Number of experimental
angles. (Integer) |
|
| fct_IDel | Element size factor function
identifier. (Integer) |
|
| El_ref | Reference element size. Default = 1.0 (Real) |
|
| c5 | Failure plastic strain in biaxial
tension (same for all directions). Default = 0.0 (Real) |
|
| Inviscid limit for the strain
rate. Default = 0.0 (Real) |
||
| CJC | Johnson-Cook strain rate
coefficient. Default = 0.0 (Real) |
|
| fct_IDrate | Strain rate dependency factor
tabulated function identifier. (Integer) |
|
| Rate_Scale | Abscissa scale factor for strain
rate dependency tabulated function. Default = 1.0 (Real) |
|
| r1 | Failure plastic strain ratio,
uniaxial compression (c1) to uniaxial tension
(c3), so
. Only used if M-Flag = 99. Default = 0.0 (Real) |
|
| r2 | Failure plastic strain ratio, pure
shear (c2) to uniaxial tension
(c3), so
. Only used if M-Flag = 99. Default = 0.0 (Real) |
|
| r4 | Failure plastic strain ratio, plane
strain tension (c4) to uniaxial tension
(c3), so
. Only used if M-Flag = 99. Default = 0.0 (Real) |
|
| r5 | Failure plastic strain ratio,
biaxial tension (c5) to uniaxial tension
(c3), so
. Only used if M-Flag = 99. Default = 0.0 (Real) |
|
| c1 | Failure plastic strain in uniaxial
compression. Default = 0.0 (Real) |
|
| c2 | Failure plastic strain in
shear. Default = 0.0 (Real) |
|
| c3 | Failure plastic strain in uniaxial
tension. Default = 0.0 (Real) |
|
| c4 | Failure plastic strain in plane
strain tension. Default = 0.0 (Real) |
|
| Inst_start | Instability start value for
localized necking. Must be entered, if S-Flag = 3. (Real) |
|
| fail_ID | (Optional) Failure criteria
identifier. (Integer, maximum 10 digits) |
Example 1
#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
# MUNIT LUNIT TUNIT
Mg mm s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 1. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW93/2/1
Steel
# RHO_I
7.8E-09
# E11 E22 E33 G12 Nu12
190000 190000 190000 70000 0.3
# G13 G23 Nu13 Nu23
70000 70000 0.3 0.3
# NL VP Fcut
0 1 0
# SigY QR1 CR1 QR2 CR2
290 580 1 200 25
# R11 R22 R12
1 1 1
# R33 R13 R23
1 1 1
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FAIL/ORTHBIQUAD/2/1
# PTHK MFLAG SFLAG NANGLE FCT_IDEL EL_REF
1 2 1 2 101 .3
# C5 DEPS0 C_JCOOK FCT_ID_RATE RATE_SCALE
0 0 0 0 0
# C1 C2 C3 C4 INST
0 0 .7 0 .3
0 0 .35 0 .15
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/101
Regularization DP450_ODG3_MED-5
0 1
1 1
6 .35
10 .35
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#enddata
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|Example 2
#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
# MUNIT LUNIT TUNIT
Mg mm s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 1. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW93/2/1
Steel
# RHO_I
7.8E-09
# E11 E22 E33 G12 Nu12
190000 190000 190000 70000 0.3
# G13 G23 Nu13 Nu23
70000 70000 0.3 0.3
# NL VP Fcut
0 1 0
# SigY QR1 CR1 QR2 CR2
290 580 1 200 25
# R11 R22 R12
1 1 1
# R33 R13 R23
1 1 1
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FAIL/ORTHBIQUAD/2/1
# PTHK MFLAG SFLAG NANGLE FCT_IDEL EL_REF
1 0 1 2 101 .3
# C5 DEPS0 C_JCOOK FCT_ID_RATE RATE_SCALE
.56 0 0 0 0
# C1 C2 C3 C4 INST
3.01 .98 .7 .42 .3
1.505 .49 .35 .21 .15
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/101
Regularization DP450_ODG3_MED-5
0 1
1 1
6 .35
10 .35
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#enddata
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|Example 3
#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
# MUNIT LUNIT TUNIT
Mg mm s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 1. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW93/2/1
Steel
# RHO_I
7.8E-09
# E11 E22 E33 G12 Nu12
190000 190000 190000 70000 0.3
# G13 G23 Nu13 Nu23
70000 70000 0.3 0.3
# NL VP Fcut
0 1 0
# SigY QR1 CR1 QR2 CR2
290 580 1 200 25
# R11 R22 R12
1 1 1
# R33 R13 R23
1 1 1
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FAIL/ORTHBIQUAD/2/1
# PTHK MFLAG SFLAG NANGLE FCT_IDEL EL_REF
1 99 1 2 101 .3
# C5 DEPS0 C_JCOOK FCT_ID_RATE RATE_SCALE
0 0 0 0 0
# r1 r2 r4 r5
4.3 1.4 .6 1.6
# C1 C2 C3 C4 INST
0 0 .7 0 .3
0 0 .35 0 .15
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/101
Regularization DP450_ODG3_MED-5
0 1
1 1
6 .35
10 .35
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#enddata
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|Comments
- For each input
direction, the failure criteria is defined using failure plastic strain
versus stress triaxiality (state of stress) as it is the case for the
/FAIL/BIQUAD criterion. This allows for the different
plastic failure strains that materials exhibit depending on loading
condition. The curve is described by 2 parabolic functions that intersect at
the triaxiality value of
which is uniaxial tension.
Figure 1. Biquad failure criterion shape 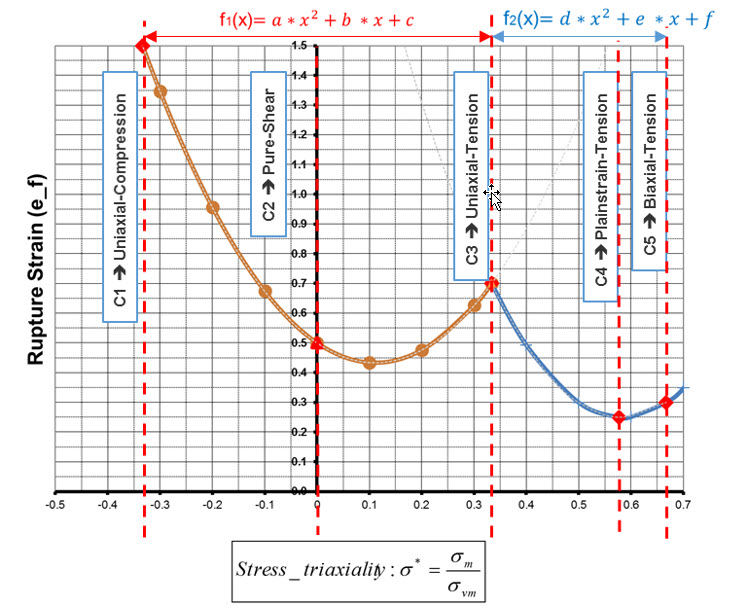
The parameters for the 2 parabolic failure strain curves versus the state of stress (stress triaxiality) are calculated iteratively by Radioss during the initialization phase using the input c1-c5 values.
If the calculated parabolic failure strain curves have negative failure strain values, these negative values will be replaced by a failure strain of 1E-6 which results in a very high damage accumulation and brittle behavior.
This failure criteria is usable for all elasto-plastic material models with shells and solids.
- To consider the
failure orthotropy, several set of c1,
c2, c3, c4 and
Inst_start parameters can be given. You can input up
to 10 different set of parameters for 10 different experimental loading
directions (marked by an angle denoted
). The number of input tested loading direction is
set by the parameter
Nangle. The directions must
be equally distributed, 1st material direction (0 degree) and 2nd material
direction (90 degrees) following the table. For isotropic material laws, the
elemental system is used: directions are distributed between the local
element x-axis (0 degree) and local element y-axis (90 degrees).
Figure 2. Expected input loading direction angle depending on the value of Nangle 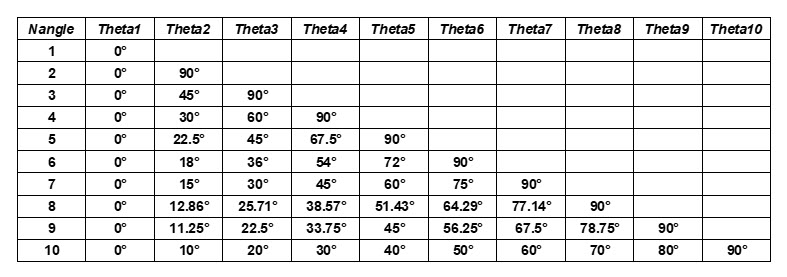
- For each input
direction, the 2 parabolic curves parameters (
,
,
,
,
,
) are computed in the Radioss Starter. During the simulation, for all
loading directions located between the input directions, a Fourier series
interpolation is used to determine the corresponding curves parameters (
,
,
,
,
,
) and, if defined, the necking instability
strain (Inst_start):
Where, are the interpolation factors for parameter . These interpolation factors are automatically computed in the Radioss Starter.
For instance, if two sets of parameters are given for the direction 0 and 90 degrees, the Fourier series interpolation enables to determine the 45 degrees curve as:Figure 3. Example of orthotropic biquad criterion shape 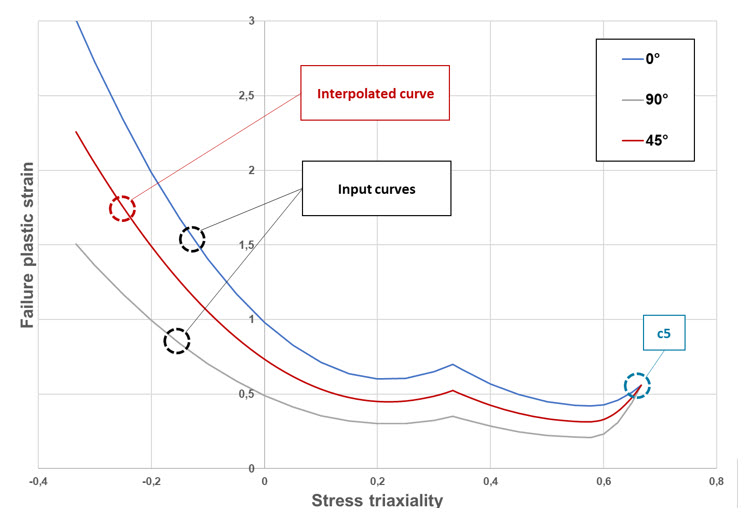
Loading directions not given in the input are interpolated using Fourier series. All directions have the same plastic strain at failure in biaxial tension.
- It must be noted that plastic strain at failure in biaxial tension c5 is common to all directions (Figure 3). Indeed, for this loading condition, the directions have no meaning as all directions are loaded in the same way. Thus, the failure behavior is the same.
- By default, values
different than 0 for c1 to c5 need to
be entered. However, specific default behaviors exist in case failure
information are missing:
- In case the material failure behavior is unknown, c1 to c5 are set to 0.0 and the mild steel behavior (M-Flag=1) is used.
- If only the tensile failure value is known, c3 is defined (c1=c2=c4=c5 = 0.0). The mild steel behavior is used and scaled by the user-defined c3 value.
- In case the material behavior is known, M-Flag is defined and c3 can be used to adjust the failure model according to the expected tensile failure. The selected material behavior is scaled by the user-defined c3 value.
- For all other cases,
all c1 to c5 are intended to
be defined and default value of 0.0 is used. Note: If c5 = 0.0, it is automatically computed depending on the value of M-Flag. In this case, the minimum value computed among all input directions will be retained.
- The plastic strain at failure from physical tests can be input as c1 – c5.
- If failure strain data
is not available then the material flag, M-Flag, can be
used to select predefined failure values for some materials.
- If
M-Flag > 0, the entered
c1, c2,
c4 and c5 values will not
be used, but will be calculated as follows, using the predefined
ratio values from the table.
- If
c3=0, the default value
shown in the table is used.
M-Flag Roughly Corresponds to Material c3 (Default)
r1 r2 r4 r5 1 Mild steel 0.60 3.5 1.6 0.6 1.5 2 HSS steel 0.50 4.3 1.4 0.6 1.6 3 UHSS steel 0.12 5.2 3.1 0.8 3.5 4 Aluminum AA5182 0.30 5.0 1.0 0.4 0.8 5 Aluminum AA6082-T6 0.17 7.8 3.5 0.6 2.8 6 Plastic PA6GF30 0.10 3.6 0.6 0.5 0.6 7 Plastic PP T40 0.11 10.0 2.7 0.6 0.7 99 Self-defined values (optional line) 0.30 Optional input Optional input Optional input Optional input Important: Neither Altair nor the authors assume any responsibility for the validity, accuracy or any results obtained from these values. You must verify your own values by reasonable test results. Usage is only recommended for early design exploration. - If c3 > 0, the selected material behavior is scaled by c3 and the r1 to r5 predefined ratio values.
- If c5 = 0.0, the minimum value of among all input directions will be retained.
- If the M-Flag = 99, failure strain ratios r1, r2, r4 and r5 must be input in a following additional line.
- If
M-Flag > 0, the entered
c1, c2,
c4 and c5 values will not
be used, but will be calculated as follows, using the predefined
ratio values from the table.
- Damage is accumulated
linearly and can be post-processed in the animation files using the output
request /ANIM/SHELL/DAMA/ALL or
/ANIM/BRICK/DAMA/111.
For shell elements when an integration point reaches , the integration points stress tensor is set to 0. Shell elements are deleted based on the value of P_thickfail.
If P_thickfail is set blank or 0, the value of P_thickfail from the shell property is used. If P_thickfail > 0, any P_thickfail value defined in the shell properties is ignored and the value entered in this failure model is used.
For values of P_thickfail set > 0, the element fails and is deleted when the ratio of through thickness failed integration points equals or exceeds P_thickfail.
In solid elements, the element is deleted when any integration point reaches .
- Special features are
activated by this flag:
- S-Flag = 1: the failure
curves are created, as shown in Comment 1. In this case, the curves may not
reach their minimum value for the same stress triaxiality (Figure 4).
Figure 4. Orthotropic biquadratic failure criterion shape when S-Flag =1 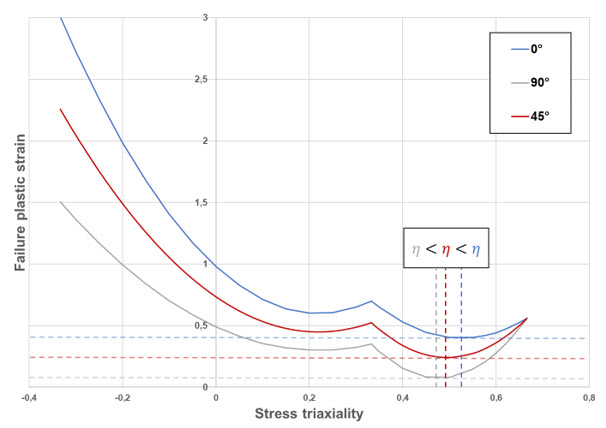
- S-Flag = 2: is set by
default. It ensures value c4 as global minimum
for all directions. To achieve this for all curves, the second
equation is split into 2 separate quadratic sub-functions where the
minimum value of the curves is at c4; where,
(Figure 5).
Figure 5. Orthotropic biquadratic failure criterion shape when S-Flag =2 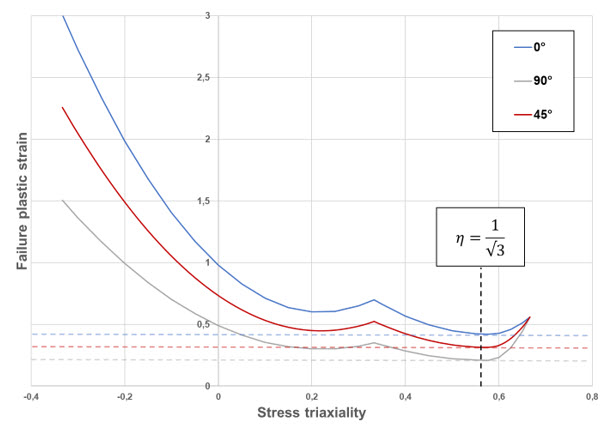
- S-Flag = 3: same as
S-Flag = 2, plus a
simplified localized necking criterion (only for shells). The
localized necking criteria is based on the Marciniak-Kuczynski
analysis. It uses two additional quadratic functions that define a
curve that represents the start of localized necking between stress
triaxiality
and
. The minimum value of this curve is
user-defined in the Inst_start field and occurs
at plane strain tension,
(Figure 6).
Using this curve, a second localized necking damage value is calculated, and failure only occurs when all integration points reach .
The Inst_start value can be estimated as the (true plastic) strain at maximum stress, from the uniaxial tension test.Figure 6. Orthotropic biquadratic failure criterion shape when S-Flag =3 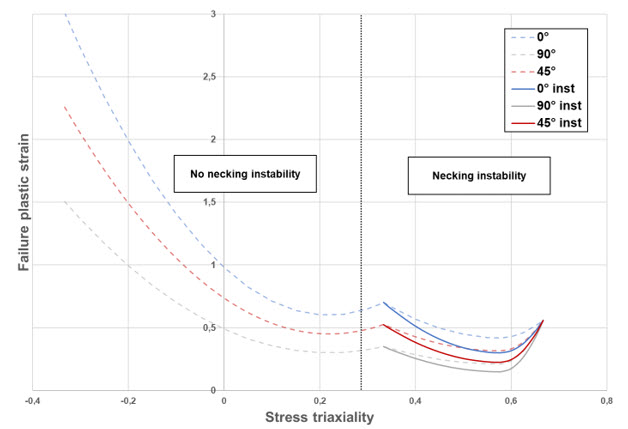
- S-Flag = 1: the failure
curves are created, as shown in Comment 1. In this case, the curves may not
reach their minimum value for the same stress triaxiality (Figure 4).
- A strain rate
dependency can be applied on the failure criterion, if:
-
and
, the Johnson-Cook’s strain rate
dependency is used. In this case, the plastic strain at failure
value is multiplied by the strain rate dependency factor
as:Where,
- Inviscid limit strain rate
- Strain rate dependency parameter
- Macaulay brackets, which considers only positive values
Note: If using a Johnson-Cook material law coupled to the /FAIL/ORTHBIQUAD criterion, the Johnson-Cook parameters used for the constitutive law might not be the same for the failure criterion. - fct_IDrate ≠
0, a tabulated function of strain rate dependency factor is used. In
this case, you have to define a function (/FUNCT)
to describe the evolution of the strain rate factor (denoted
) with the strain rate. You can also
input a strain rate scale factor for the abscissa of the function:
Xscale_rate (by default, this scale factor is
set to 1.0). Using the tabulated strain rate dependency, the damage
variable computation becomes:
Important: The strain rate dependency applied to the failure criterion can only be used with material laws that are strain rate dependent. The strain rate used for the constitutive law (total strain rate, deviatoric strain rate or plastic strain rate), will be the same used for the failure criterion. -
and
, the Johnson-Cook’s strain rate
dependency is used. In this case, the plastic strain at failure
value is multiplied by the strain rate dependency factor
as:
- The fail_ID is used with /STATE/BRICK/FAIL and /INIBRI/FAIL. There is no default value. If the line is blank, a value will not be output for failure model variables in the /INIBRI/FAIL (written in .sta file with /STATE/BRICK/FAIL option).
- If non-local regularization is used (with /NONLOCAL/MAT), the element size scaling factor is not used. If a scaling function is still defined (fct_IDel > 0), the parameters are scaled using LE_MAX parameter of the non-local card (either specified directly by you or computed from the Rlen parameter value).