Constraint: PTCV
Model ElementConstraint_PTCV defines a higher pair constraint. A fixed point on one body slides on a curve that is fixed on a second body. The point is not allowed to lift off the curve.
Format
<Constraint_PTCV
id = "integer"
[ label = "string" ]
i_marker_id = "integer"
j_marker_id = "integer"
[ disp_xo = "real" ]
[ disp_yo = "real" ]
[ disp_zo = "real" ]
[ vel_o = "real" ]
[ zi_direction = {"PERPENDICULAR" | "PARALLEL"} ]
curve_id = "integer"
/>Attributes
- id
- Element identification number, (integer>0). This number is unique among all Constraint_PTCV elements.
- label
- The name of the Constraint_PTCV element.
- i_marker_id
- Specifies a Reference_Marker that defines the connection on the first body.
The origin of this Reference_Marker defines the point that is
required to slide on the curve. The body containing this
Reference_Marker may be a rigid body, a flexible body or a point
body.
The parameter is mandatory.
- j_marker_id
- Specifies a Reference_Marker that defines the coordinate system in which the
curve points are defined. The curve is defined on the body containing this
Reference_Marker and moves with this body. The body containing the
curve must be a rigid body or a point body.
The parameter is mandatory.
- disp_x0, disp_y0, disp_z0
- Defines a guess for the initial contact point on the curve. The coordinates are measured with
respect to the global origin and are defined in the global coordinate system.
This parameter is optional. See Comment 2 for how this data is used.
- vel_0
- Defines the initial sliding velocity of the origin of i_marker_id with
respect to j_marker_id along the tangent at the contact point, as
measured by an observer on the curve, placed at the contact point.
This parameter is optional. See Comment 4 for how this data is used.
- zi_direction
- Enforces the z-axis of i_marker_id to be either PERPENDICULAR (normal) or PARALLEL (tangential) to the curve. If this parameter is not defined, the orientation of the z-axis in respect to the curve can be arbitrary.
- curve_id
- The ID of the curve that is fixed on the second body.
Example

- The system is modeled in length units of millimeters, and time units of seconds.
- The curve is defined in the global coordinate system, and is represented by Reference_ParamCurve 1.
- The curve is defined in the coordinate system of Reference_Marker 21, which belongs to ground.
- Reference_Marker 11 defines the tip of the end effector.
- The initial contact point on the curve, defined with respect to the global coordinate system, is [263.2, 1342.7, 2343.02].
- The initial sliding velocity of the point along the curve is 50.23 mm/sec.
The Constraint_PTCV object for the above system is:
<Constraint_PTCV
id = "1"
i_marker_id = "11"
j_marker_id = "21"
disp_xo = "263.2"
disp_yo = "1342.7"
disp_zo = "2343.02"
vel_o = "50.23"
curve_id = "1"
/>Comments
- Constraint_PTCV defines a higher pair
constraint, where a fixed point on one body (Body-1) is required to slide along a curve
defined on a second body (Body 2). This is shown schematically in the image below. The curve
can be 3D and is represented parametrically using a Reference_ParamCurve
element.
Figure 2. An illustration of a Point-on-Curve Constraint 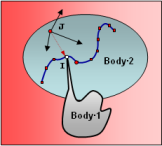
The origin of marker I defines a fixed point on Body-1. Body-1 may be any kind of body - Body_Rigid, Body_Flexible or Body_Point.
The curve is "etched" on Body-2. The curve points remain fixed with respect to Body-2 and are defined in the coordinate system of Reference_Marker J.
- The attributes disp_x0,
disp_y0 and disp_z0 define the initial contact point
on the curve. This point, denoted as P0 in the image below, need not lie exactly
on the curve.MotionSolve finds the point P on the curve that is closest to P0. The initial point on the curve is used to calculate an initial value of the curve parameter α0. An iterative process is then used to locate P.
Figure 3. Calculation of the Initial Contact Point P0 - If you select P0 to be near either end of the curve, there is a chance that when the curve parameter is perturbed, it falls outside the bounds of the curve. This causes a fatal error in MotionSolve. To avoid this, use a longer curve to allow room for perturbations.
- The attribute vel_0 defines the velocity of the contact point on the curve as seen by an observer on the body containing the curve. This data is used to generate an initial value for the time derivative of the curve parameter. A positive value implies that the slip is in the direction of the instantaneous tangent which points along the direction of increasing curve parameter. A negative value implies the direction of slip is in the opposite direction to the instantaneous tangent vector. This is shown in the image above.
- The constraint does not ensure that the contact point will stay within the range of data specified for the curve. Additional forces at the end need to be defined by the user to satisfy this requirement.
- Both open and closed curves are supported. For a closed curve, the first and last points must be the same.
- The curves are required to be smooth to second order. In other words, have continuous first and second derivatives with respect to the curve parameter everywhere. A non-smooth curve will cause numerical difficulties.
- The function PTCV(...) may be used to extract a component of the reaction force at the contact point in any direction. See MotionSolve Functions for more information.
- Constraint_PTCV does not permit lift-off. You can look at the reaction force to determine if there is a tendency for the point follower to lift-off the curve. If the component of the reaction force along the common normal is positive, the "contact" force is repulsive. If the component is negative, the "contact" force is attractive, and therefore the point-follower would have separated from the curve if the constraint were not there.
- If you notice an "attractive" reaction force, you might consider modeling the subsystem using the Force_Contact object that allows lift-off to occur.
