Constraint: CVSF
Model ElementConstraint_CVSF defines a higher pair constraint. A curve on one body slides on a surface that is fixed to a second body. The curve is not allowed to lift off the surface.
Format
<Constraint_CVSF
id = "integer"
label = "Name of Constraint_CVSF element"
i_marker_id = "integer"
[
i_disp_xo = "real"
i_disp_yo = "real"
i_disp_zo = "real"
]
curve_id = "integer"
j_marker_id = "integer"
[
j_disp_xo = "real"
j_disp_yo = "real"
j_disp_zo = "real"
]
surface_id = "integer" >
/>Attributes
- id
- The element identification number (integer>0). This number is unique among all Constraint_CVSF elements.
- label
- The name of the Constraint_CVSF element.
- i_marker_id
- Specifies a Reference_Marker that serves as the coordinate system for the definition of the curve. The body containing this Reference_Marker can be of type flexible, rigid, or point. The parameter is mandatory.
- i_disp_x0, i_disp_y0, i_disp_z0
- Defines a guess for the initial contact point on the curve. The coordinates are measured with respect to i_marker_id and are defined in its coordinate system. The parameter is optional. 2
- curve_id
- Defines the ID of the Reference_ParamCurve object that contains the curve data points. The parameter is mandatory.
- j_marker_id
- Specifies a Reference_Marker that defines the the coordinate system in which the surface points are defined. The surface is fixed to the body containing this Reference_Marker and moves rigidly with this body. The body containing the curve can be flexible, rigid or point body. The parameter is mandatory.
- j_disp_x0, j_disp_y0, j_disp_z0
- Defines a guess for the initial contact point on the surface. The coordinates are measured with respect to j_marker_id and are defined in its coordinate system. The parameter is optional. 5
- surface_id
- Defines the ID of the Reference_ParamCurve object that contains the surface data points. The parameter is mandatory.
Example
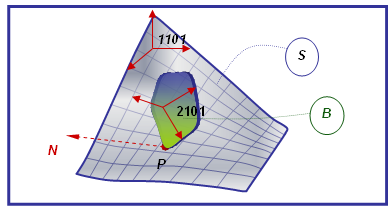
The thickness of solid B is very small. For all practical purposes, it can be represented as a curve.
- Assume the ID of the curve on Body B is 201.
- The curve points are defined with respect to Reference_Marker 2101.
- Assume the contact point P on the curve has coordinates of [0.2, -0.8, 0.1] with respect to the Origin of 2101. The coordinates are measured in the coordinate system of 2101.
- Assume the ID of the surface S is 101.
- The surface points of S are defined with respect to a Reference_Marker 1101.
- Assume the contact point P on the Surface S has coordinates of [0.3, -3.0, 1.1] with respect to the Origin of 1101. The coordinates are measured in the coordinate system of 1101.
The Constraint_CVSF object for the above description is:
<Constraint_CVSF
id = "1"
label = "Name of Constraint_CVSF element"
i_marker_id = "2101"
i_disp_x0 = "0.2"
i_disp_y0 = "-0.8"
i_disp_z0 = "0.1"
curve_id = "201"
j_marker_id = "1101"
j_disp_x0 = "0.3"
j_disp_y0 = "3.0"
j_disp_z0 = "1.1"
surface_id = "101" >
/>Comments
- Constraint_CVSF defines
a higher pair constraint. A curve defined on one body is required to roll
and slide on a surface defined on a second body.
The curve is represented parametrically using a Reference_ParamCurve object. The curve-points are defined with respect to the origin of Reference_Marker I. The point coordinates are measured in the coordinate system associated with Reference_Marker I. The curve is required to be fixed with respect to the body containing I and moves with it.
The surface is represented parametrically using a Reference_ParamCurve object. The surface points are defined with respect to the origin of Reference_Marker J. The point coordinates are measured in the coordinate system associated with Reference_Marker J. The surface is required to be fixed with respect to the body containing J and moves with it.
- The attributes
i_disp_x0, i_disp_y0 and
i_disp_z0 define the initial contact point on the
curve. This point, denoted as P0 in the image below, need not
exactly be on the curve. MotionSolve finds the
nearest point on the curve P to P0. The initial point on the
curve is used to calculate an initial value of the curve parameters
α0. An iterative process is used.
Figure 2. Calculation of the Initial Contact Point P (α0) on the Curve - Both open and closed curves are supported. For a closed curve, the first and last points must be the same.
- The curve is required to be smooth to second order. In other words, have uniquely defined first and second derivatives with respect to the curve parameter everywhere. A non-smooth curve causes numerical difficulties.
- The attributes
j_disp_x0, j_disp_y0, and
j_disp_z0 define the initial contact point on the
surface. This point, denoted as P0 in the image below, need not
exactly be on the surface. MotionSolve finds
the nearest point on the curve P to P0. The initial point on the
surface is used to calculate an initial value of the surface parameters
u0 and v0. An iterative process is used.
Figure 3. Calculation of the Initial Contact Point P (u0, v0) on a Surface 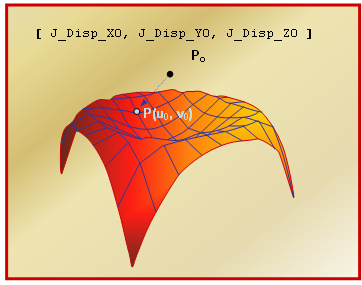
- The surface is required to be smooth to second order. In other words, to have a uniquely defined first and second derivatives with respect to the surface parameters everywhere. A non-smooth surface causes numerical difficulties.
- Both open and closed surfaces are supported. A surface may be closed in one or both of the parameters.
- Constraint_CVSF does not ensure that the contact point stays in the range of data specified for the curve or the surface. Additional forces at the boundaries need to be defined to meet this requirement.
- The function CVSF may be used to extract a component of the reaction force at the contact point in any direction.
- Constraint_CVSF does not permit lift-off. You can look at the reaction force to determine if there is a tendency for the point follower to lift-off the curve. If the component of the reaction force along the normal to the surface or the curve at the contact point is positive, the "contact" force is repulsive. If the value is negative, the "contact" force is attractive, and therefore the bodies would have separated from the curve if the constraint were not there.
- If you notice an "attractive" reaction force, you might consider modeling the subsystem using the Force_Contact object that allows lift-off to occur.
