Reference: PlantState
Model ElementReference_PlantState defines a list of user-defined states used in generating a linear representation of a model about an operating point. The linear representation is used for both eigenvalue analysis and state matrix generation.
Format
<Reference_PlantState
id= "integer"
[label= "string"]
num_element= "integer"
variable_id_list= "integer, integer, ..., integer"
/>Attributes
- id
- Specifies the element identification number. This number is unique among all Reference_PlantState elements.
- label
- An optional string that describes the name of the Reference_PlantState element. The description is primarily used to make the input more readable.
- num_element
- Number of states that are specified in this Reference_PlantState element.
- variable_id_list
- Specifies the IDs of the variables that define the states that are to be used in the linear analysis. The number of variable IDs specified in the list must be exactly equal to num_element.
Comments
- The eigenvalues and eigenvectors of many systems, especially rotating
systems, depend on the states that are chosen to linearize the equations of
motion. Often, a preferred set of states, corresponding to what is normally
experimentally measured, are desired for linearization. PSTATE is one method
that you can use to specify these states.
Using a set of states different from those corresponding to what was measured does not yield wrong results. The MotionSolve results are correct, but they are not expected.
See the example for a physical system where the eigenvalues and eigenvectors depend on the states used to linearize the system.
- The state matrices [A], [B], and [C] also depend on the states that are used
for representing the linearized multibody system. To understand this,
consider a set of state matrices for states x, inputs u, and outputs y. The
state-space representation for such a system is:
If a new set of states are chosen, then the state space equations with states z are:
, where
See the example for a physical system where user-defined states are used to compute the system state matrices at an operating point.
- The number of states specified in variable_id_list and
num_element can be greater than, equal to, or less
than the number of degrees of freedom (
NDOF) of the system. Three possibilities exist:- num_element <
NDOFIn this case, MotionSolve uses all the states specified in Reference_PlantState in the linear equation formulation. Since the linear problem must be defined in terms of
NDOFstates, the additionalNDOF- num_element states required to formulate the linear problem are automatically selected by MotionSolve. - num_element =
NDOFIn this case, MotionSolve uses all the states specified in Reference_PlantState in the linear equation formulation. Since all degrees-of-freedom have been completely specified, MotionSolve only uses these states to formulate the linear problem.
- num_element >
NDOFIn this case, MotionSolve uses only
NDOFstates specified in Reference_PlantState in the linear equation formulation. MotionSolve warns that you have specified too many states to use. The extra num_element -NDOFstates are discarded and the problem is solved.
- num_element <
- The expressions defining the Variables in
variable_id_list in a PSTATE can only be a function
of displacements or angular measures.The following is a valid definition of PSTATE:
<Reference_Variable id = "71" type = "EXPRESSION" expr = "DM(11,12)" /> <Reference_Variable id = "72" type = "EXPRESSION" expr = "DX(22,33,44)" /> <Reference_Variable id = "73" type = "EXPRESSION" expr = "AZ(55,66)" /> <Reference_PlantState id = "7", num_element = "3" variable_id_list = “71, 72, 73” />The following is an invalid definition of PSTATE. Variable 82 is a function of velocity and Variable 83 is a function of an acceleration.<Reference_Variable id = "81" type = "EXPRESSION" expr = "DM(11,12)" /> <Reference_Variable id = "82" type = "EXPRESSION" expr = "VX(22,33,44)" /> <Reference_Variable id = "83" type = "EXPRESSION" expr = "ACCZ(55,66)" /> <Reference_PlantState id = "8", num_element = "3" variable_id_list = “81, 82, 83” />MotionSolve flags invalid PSTATE definitions as errors and stops execution.
- The expressions defining the Variables in
variable_id_list in a PSTATE must be linearly
independent. Consider the following definition of
PSTATE:
<Reference_Variable id = "91" type = "EXPRESSION" expr = "Dx(71,62)" /> <Reference_Variable id = "92" type = "EXPRESSION" expr = "2* Dx(71,62)" /> <Reference_PlantState id = "9", num_element = "2" variable_id_list = “91, 92” />You can easily verify that VARIABLE id=92 is linearly dependent on VARIABLE id=91. In fact, it is always twice the value of VARIABLE id=91. Knowing one, you can always use this relationship to compute the other. The second VARIABLE does not provide any new information.
In such cases, MotionSolve warns you that one of the user-defined states is linearly dependent on the other states. MotionSolve ignores the dependent state. If necessary, it will pick an internal state as a replacement to use for linearization.
Examples
- The hub of the helicopter rotor, shown as a blue disk of radius e, rotates about its center O, with an angular velocity ω in the counter-clockwise direction about the global Z-axis.
- A helicopter blade B, shown in orange, is attached to the hub with a
revolute joint. The blade has length 2L,
mass m, and moment of inertia
I about its center-of-mass
B* and about the global Z-axis.
Figure 1. 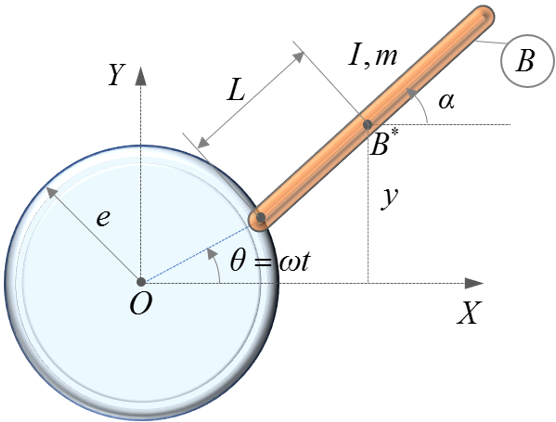
- Choose the angle of the blade to the global X, α, as the state.
- Alternatively, you can choose the global y-coordinate of point B*, y, as the state.
| State α | State y |
|---|---|
| Equations of Motion
|
|
| Operation Point
|
Operation Point
|
| [A] Matrix
|
[A] Matrix
|
| Eigenvalues for:
|
Eigenvalues for:
|
Let MARKER 34 be placed at B*. Its x-axis is along the blade length, and its z-axis along the global z.
- Define α in a
VARIABLE:
<Reference_Variable id = "22" type = "EXPRESSION" expr = "AZ(34)" /> - Tell MotionSolve to use α
to generate the linearized
equations:
<Reference_PlantState id = “3010” num_element = “1” variable_id_LIST = “22”/>
NUMBER NATURAL_FREQ(HZ) DAMPING_RATIO REAL(HZ) IMAG_FREQ(HZ)
1 7.001886E-01 0.000000E+00 0.000000E+00 7.001886E-01
1 7.001886E-01 0.000000E+00 0.000000E+00 -7.001886E-01A = [0.00000000000000000E+00, 1.00000000000000000E+00;
-1.93548505949367993E+01,-1.91975649453440089E-06]- Define y in a
VARIABLE:
<Reference_Variable id = "22" type = "EXPRESSION" expr = "DY(34)" /> - Tell MotionSolve to use y
to generate the linearized
equations:
<Reference_PlantState id = “3010” num_element = “1” variable_id_LIST = “22” />
NUMBER NATURAL_FREQ(HZ) DAMPING_RATIO REAL(HZ) IMAG_FREQ(HZ)
1 1.738762E+00 0.000000E+00 0.000000E+00 1.738762E+00
1 1.738762E+00 0.000000E+00 0.000000E+00 -1.738762E+00A = [0.00000000000000000E+00, 1.00000000000000000E+00;
-1.19354838709666097E+02, 1.71456230219270937E-13]