Courbe 2D : intégrale
Introduction
L'utilisateur peut représenter le résultat du calcul de l'intégrale des fonctions de grandeurs spatiales ou de paramètres entrée/sortie en forme de courbes.
Fonctionnement
Les courbes de l'intégrale sont générées de la façon suivante :
| Phase | Description |
|---|---|
| 1 | La commande Intégrale d'une courbe 2D est appliquée à une courbe élémentaire ou à un ensemble des courbes élémentaires de l'entité courbe 2D |
| 2 | La primitive de chaque courbe analysée est construite par le calcul de l'intégral en chaque point de l'intervalle de définition de la courbe |
| 3 | Les nouvelles courbes élémentaires sont rajoutées à l'ensemble des courbes déjà existantes de la courbe 2D |
Principe
L'intégrale est calculée à partir de la fonction représentée par la courbe existante. L'intégration est faite suivant la méthode des trapèzes.
Soit une courbe représentant une fonction f, le calcul de l'intégrale en chaque point est réalisé comme suit :
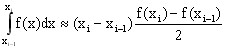
Le nombre de points de la courbe de l'intégrale est le même que celui de la courbe initiale.
L'ordonnée du premier point de la courbe de l'intégrale est toujours nulle.
Il faut que les valeurs en abscisse soient strictement croissantes (b>a).
Méthode des trapèzes : rappel
La méthode des trapèzes est une
méthode permettant de réaliser le calcul numérique
d'une intégrale 
.
Le principe est d'approcher la région sous la courbe représentative de la fonction f par un trapèze et d'en calculer l'aire :
Pour obtenir de meilleurs résultats, on découpe l'intervalle [a,b] en n intervalles plus petits et on applique la méthode sur chacun d'entre eux.
Calculer l'intégrale d'une courbe 2D
Pour calculer (et tracer) l'intégrale d'une courbe 2D, suivre les instructions suivantes :
| Etape | Action |
|---|---|
| 1 |
Dans le menu :
|
| → | Une boite de sélection est ouverte |
| 2 |
Dans la boîte de sélection :
|
| 3 |
Dans la boîte Intégrale d'une courbe 2D :
|
| → | Une ou plusieurs courbes de l'intégrale sont calculées et affichées dans la feuille de la courbe 2D. |