Symmetries

Symmetry entities define planes of symmetry within a model so that morphs can be applied in a symmetric fashion.

Symmetries do not have an active or export state.

Create Symmetries

Create symmetries that influence handles, morph volumes, domains, blocks, rwalls, and shapes.

  1. From the Morph ribbon, click the triangle next to the Morph group name and select Symmetries.
    The Morph: Symmetries dialog opens.
  2. Define the symmetry.
    Table 1.
    Option Action
    Name Enter a name for the new symmetry that you wish to create.
    Type Pick the type of symmetry you wish to create.
    Linking Direction For reflective symmetries (1-, 2-, or 3-plane, or cyclical), choose how different sides of the symmetry interact with each other.
    • Unilateral symmetries have one and only one side that governs the others, but not vice versa. For example, handles created and morphs applied to handles on the positive side of the symmetry are reflected onto the other side or sides of the symmetry, but handles created or morphs applied to handles on the other side or sides of the symmetry are not reflected.
    • For multilateral symmetries, all sides govern all other sides. For example, a handle created or a morph applied to a handle on any side is reflected to all the other sides.
    Linking Method For reflective symmetries (1-, 2-, or 3-plane, or cyclical), choose how strict the symmetric requirements should be.
    • Approximate symmetries may contain handles that are not symmetric to other handles. For example, handles created on any side of the symmetry are not reflected to the other sides. This option is best for asymmetrical, but similar, domains or for a cyclical symmetry applied to a mesh that sweeps through an arc but not a full circle.
    • Enforced symmetries cannot contain handles that are not symmetric on all other sides. For example, handles created or deleted on any side of the symmetry are created or deleted on the other sides so that the symmetry is maintained. When a reflective symmetry is created with the enforced option, additional handles may also be created to meet the enforcement requirements.
    Note: Handles created due to the enforced option may not be located on any mesh, however, they will always be assigned to the nearest domain and will affect nodes in that domain.
    System Select a coordinate system with which the symmetry is aligned.
    Align With Define which axis of the chosen system the symmetry is aligned with: the default axis, or one of its x, y, or z axes.
    Affected Domains Select the domain(s) that the new symmetry is part of.
    Morph Volumes and Mapping By default, symmetries do not affect morph volumes or map to geom operations. If you wish the symmetry to affect morph volumes and mapping operations as well as domains, select this check box. Symmetries that affect morph volumes will affect all of the morph volumes in the model. Symmetries that affect mapping operations will affect all mapping operations, even if there are no domains in the model.
    Color Select a color for the symmetry's icon.
    Size Specify a size for the symmetry's visual icon. This only affects the appearance of the symmetry icon in the modeling window.
  3. Click Create.

Symmetry Types

HyperMesh supports reflective and non-reflective symmetries.

There are two basic symmetry groups: reflective and non-reflective. Symmetries can be combined, but you must be careful not to create confusing symmetrical arrangements. Symmetries can also be applied to unconnected domains. In this case, the symmetric handle linking works the same as that for connected domains, but the influences between handles and nodes for non-reflective symmetries do not extend across to all domains.

Reflective Symmetries

Reflective symmetries link handles in a symmetric fashion so that the movements of one handle will be reflected and applied to the symmetric handles. You can also use reflective symmetries to reflect morphs performed on domains when using the alter dimensions.

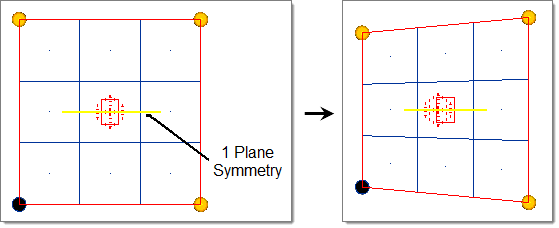
Reflective symmetries are one plane, two plane, three plane, and cyclical.
One Plane
A mirror is placed at the origin perpendicular to the selected axis (default = x-axis).
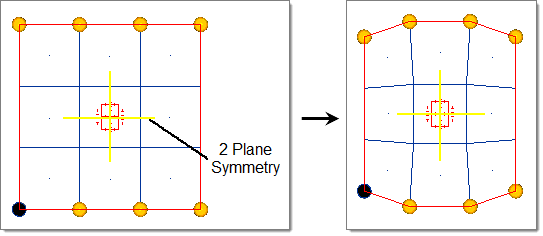
In Figure 1, the mesh on the left is before morphing; the mesh on the right is after morphing. The icon for 1-plane symmetry is a rectangle perpendicular to the symmetry system's selected axis. You can think of this rectangle as a mirror. The highlighted handle is moved. Notice how only the handle at the lower left has been selected and how the handle on the upper left is automatically moved symmetrically. This type of symmetry is very useful for a wide variety of symmetric models.
Figure 1.


Two Plane
Two mirrors are placed at the origin perpendicular to the selected axis and the subsequent axis (that is x and y, y and z, z and x) (default = x and y-axis).
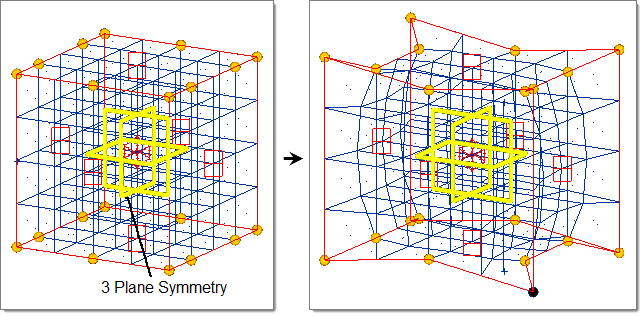
In Figure 2, the mesh on the left is before morphing; the mesh on the right is after morphing. The icon for 2-plane symmetry is two rectangles perpendicular to the symmetry system's selected axis and subsequent axis. You can think of these rectangles as mirrors. The highlighted handle is moved. Notice how only the handle at the lower left has been selected and how the other three symmetric handles are automatically moved symmetrically. This type of symmetry is very useful for objects symmetric across two perpendicular planes.
Figure 2.


Three Plane
Three mirrors are placed at the origin perpendicular to all three axes.
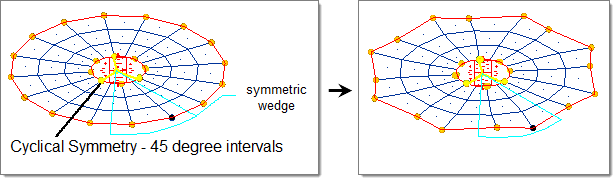
In Figure 3, the mesh on the left is before morphing; the mesh on the right is after morphing. The icon for 3-plane symmetry is three rectangles perpendicular to all three of the symmetry system axes. You can think of these rectangles as mirrors. The highlighted handle is moved. Notice how only the handle at the lower right has been selected and how the other seven symmetric handles are automatically moved symmetrically. This type of symmetry is very useful for objects symmetric across three perpendicular planes.
Figure 3.


Cyclical
Two mirrors are placed along the selected axis (default = z-axis) and running through the origin with a given angle in between that is a factor of 360. The result is a wedge that is reflected a certain number of times about the selected axis.
Figure 4 is an example of cyclical symmetry with a cyclical frequency of 8 (45 degrees per wedge). The mesh on the left is before morphing and the mesh on the right is after morphing. The icon for cyclical symmetry is a number of spheres lying perpendicular the symmetry system's selected axis and connected to the origin with lines. The number of spheres is equal to the number of symmetric wedges. Each cyclical wedge is identical to the others when rotated through an angle (in this case 45 degrees) about the selected axis. The highlighted handle is moved. Notice how only one handle has been selected and how the other seven symmetric handles are automatically moved symmetrically. This type of symmetry is very useful for objects that repeat at regular intervals about a central point.
Figure 4.


Reflective symmetries can be defined as either unilateral or multilateral and either approximate or enforced.
Unilateral Symmetries
One side governs the other, but not vice versa.
For example, handles created and morphs applied to handles on the positive side of the symmetry are reflected onto the other side or sides of the symmetry, but handles created or morphs applied to handles on the other side or sides of the symmetry are not reflected.
Multilateral Symmetries
All sides govern all other sides.
For example, a handle created or a morph applied to a handle on any side is reflected to all the other sides.
Approximate Symmetries
Contain handles that are not symmetric to other handles. This option is best for asymmetrical, but similar, domains or for a cyclical symmetry applied to a mesh that sweeps through an arc but not a full circle.
For example, handles created on any side of the symmetry are not reflected to the other sides.
Enforced Symmetries
Cannot contain handles that are not symmetric on all other sides.
For example, handles created or deleted on any side of the symmetry are created or deleted on the other sides so that the symmetry is maintained. When a reflective symmetry is created with the enforced option, additional handles may also be created to meet the enforcement requirements.
Note: Handles created due to the enforced symmetry may not be located on any mesh, however, they will always be assigned to the nearest domain and will affect nodes in that domain.

Non-Reflective Symmetries

Non-reflective symmetries are linear, circular, planar, radial 2D, cylindrical, radial + linear, radial 3D, and spherical. These change the way that handles influence nodes as well as link the symmetric handles so that the movement of one affects the others.

Generally speaking, the handles for a domain with non-reflective symmetry will act as if they are the shape of the symmetry type. For instance, a domain with linear symmetry causes handle movements to act on the domain as if the handle was a line in the direction of the x-axis. A domain with circular symmetry causes handle movements to act on the domain as if the handle was a circle centered around the z-axis. The edges of a domain affect how influences between handles and nodes are calculated. Non-reflective symmetries work best for domains that are shaped like the symmetry type and have a regular mesh. For example, a circular symmetry works best for a round domain with a concentric mesh.

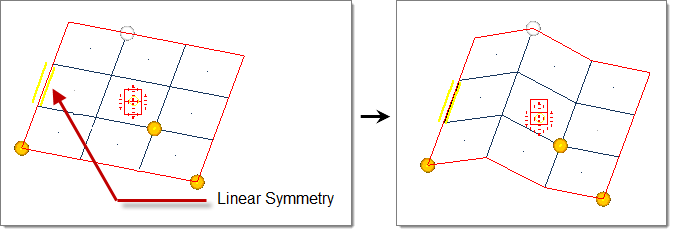
Non-reflective symmetries are linear, circular, planar, radial 2D, cylindrical, radial + linear, radial 3D, and spherical.
Linear
Handle acts as a line drawn through the handle location parallel to the selected axis (default = x-axis).
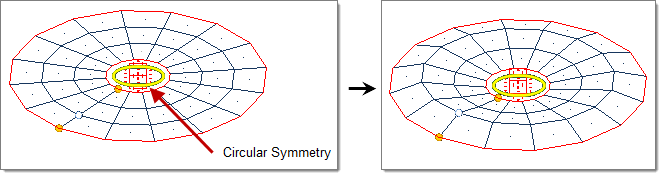
In Figure 5, the mesh on the left is before morphing; the mesh on the right is after morphing. The icon for linear symmetry is two parallel lines extending along the selected axis. The highlighted handle is moved. Notice how the handles act on the mesh as if they were parallel lines. This type of symmetry is very useful for changing the shape of entire cross-sections by moving only a few handles.
Figure 5.


Circular
Handle acts as a circle drawn through the handle position about the selected axis (default = z-axis).
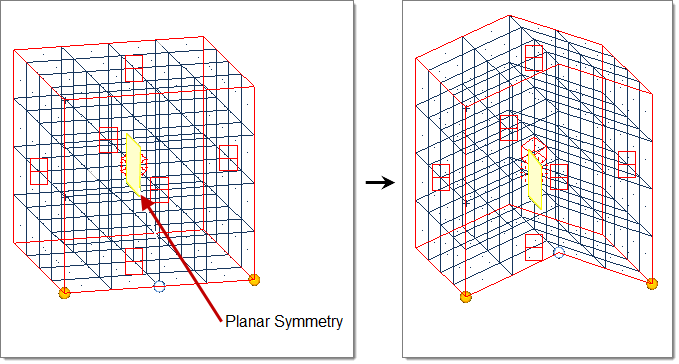
In Figure 6, the mesh on the left is before morphing; the mesh on the right is after morphing. The icon for circular symmetry is a circle at the origin of the symmetry system lying perpendicular to the selected axis. The highlighted handle is moved. Notice how the handles act on the mesh as if they are circles about the selected axis. This type of symmetry is very useful for keeping a circular part circular while manipulating its shape.
Figure 6.


Planar
Handle acts as a plane drawn through the handle location perpendicular to the selected axis (default = x-axis).
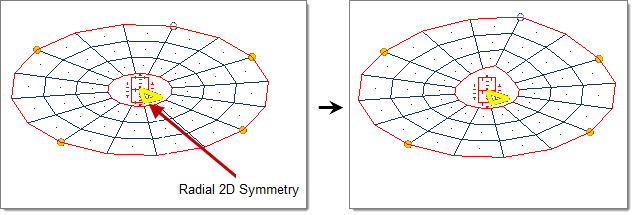
In Figure 7, the mesh on the left is before morphing; the mesh on the right is after morphing. The icon for planar symmetry is a shaded rectangle perpendicular to the symmetry system's selected axis. The highlighted handle is moved. Notice how the handles act on the mesh as if they were perpendicular planes. This type of symmetry is very useful for manipulating the shape of regular sections along their length without changing their profile.
Figure 7.


Radial 2D
Handle acts as a ray drawn through the handle position originating from and extending perpendicular to the selected axis (default = z-axis).
In Figure 8, the mesh on the left is before morphing; the mesh on the right is after morphing. The icon for radial 2-D symmetry is a flat cone with its vertex at the symmetry system origin and perpendicular to the selected axis. The highlighted handle is moved. Notice how the handles act on the mesh as if they were rays extending in a radial direction away from the selected axis. This type of symmetry is very useful for changing the shape of a part while keeping its radial profile intact.
Figure 8.


Cylindrical
Handle acts as a cylinder drawn through the handle position about the selected axis (default = z-axis).
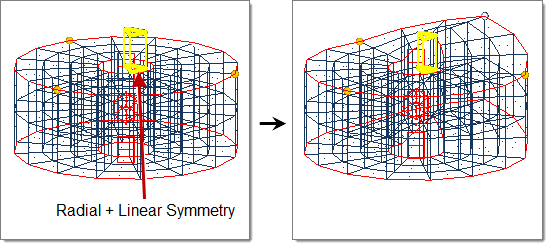
In Figure 9, the mesh on the left is before morphing; the mesh on the right is after morphing. The icon for cylindrical symmetry is a cylinder parallel to the symmetry system's selected axis centered about the origin. The highlighted handle is moved. Notice how the handles act on the mesh as if they were cylinders. This type of symmetry is the equivalent of using both circular and linear symmetry together and is very useful for making circular changes to solid meshes.
Figure 9.


Radial + Linear
Handle acts as a plane drawn through the handle position extending from the selected axis (default = z-axis).
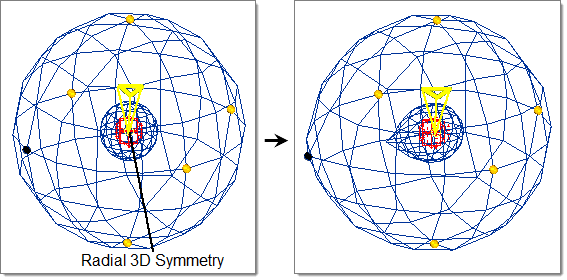
In Figure 10, the mesh on the left is before morphing; the mesh on the right is after morphing. The icon for radial+linear symmetry is a 3-D wedge lying perpendicular to the selected axis with its vertex at the symmetry system origin. The highlighted handle is moved. Notice how the handles act on the mesh as if they were planes parallel to and extending away from the selected axis. This type of symmetry is the equivalent of using both radial and linear symmetry together and is very useful for making radial changes to solid meshes.
Figure 10.


Radial 3D
Handle acts as a ray drawn through the handle position originating from origin.
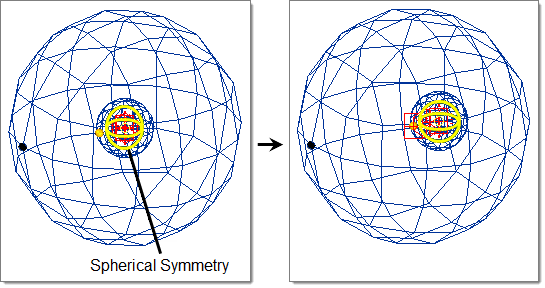
Figure 11 is an example of radial 3-D symmetry. The model is a hollow sphere made with solid elements. The mesh on the left is before morphing; the mesh on the right is after morphing. The icon for radial 3-D symmetry is a cone with its vertex at the origin of the symmetry system. The highlighted handle is moved. Notice how the handles act on the mesh as if they were rays extending away from the origin. This type of symmetry is very useful for making radial changes to spherical objects.
Figure 11.


Spherical
Handle acts as a sphere drawn through the handle position centered on the origin.
In Figure 12, the mesh on the left is before morphing; the mesh on the right is after morphing. The model is a hollow sphere made with solid elements. The icon for spherical symmetry is a sphere centered at the symmetry system origin. The highlighted handle is moved. Note how the handles act on the mesh as if they were spheres centered at the origin. This type of symmetry is useful for changing the shape of spherical objects while keeping their spherical shape intact.
Figure 12.