First Ply Failure Method

The Panel_composite config comes with a set of various composite laminates first ply failure criteria. All of these failure criteria are bundled in a single certification method called “First_Ply_Failure”. This method internally invokes former ESAComp engine.

Despite the method being available under the Panel_composite config, it evaluates failure criteria per element basis. As mentioned before, if the structural property assigned to a given designpoint refers to a user-defined property (PCOMP or PCOMPG), then all attributes required by the method are queried from this property. Otherwise, it will go directly per element’s property. Details on the supported properties can be found in Solver Specific Details in Composite Stress Toolbox.

All composite stresses are recalculated from shell element forces and moments based on the reference laminate property used. It then requires that result files contain shell element resultant forces and moments.

Math

Shell element resultant forces and moments (F/M/Q) are read from the result file and translated to the material orientation system based on the model. The moment sign conversion follows the notation used in 1. Resultant forces and moments are translated to the geometrical mid-plane of the laminate. For ply-based models, local zone-laminates are automatically created. Strains and stresses are resolved at the three recovery planes of each layer using the Classical Lamination Theory. Out-of-plane shear stresses are determined based on 2 when needed. First ply failure-based analysis is performed for the selected design criteria and material combinations with single or multiple loadcases. For the required strength allowable, refer to Figure 1.
Figure 1. Required Allowable Per Criteria


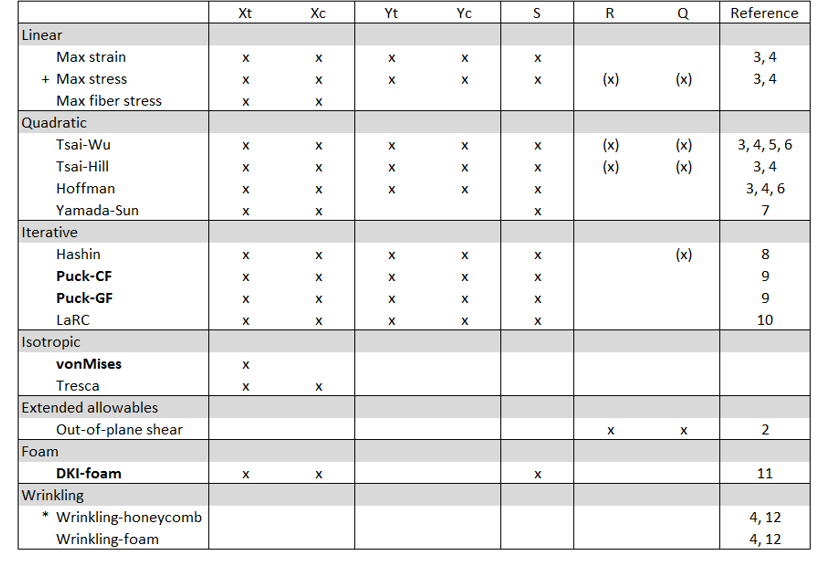
+ Max stress for isotropic material requires Xt, Xc, and S and considers out-of-plane shear.

HM metadata values
  • R= Transverse_Shear_Allowable_S13
  • Q= Transverse_Shear_Allowable_S23
  • *E3

The bold design criteria automatically consider out-of-plane shear stresses.

If R and Q (for MAT8) are defined, traditional in-plane criteria will also consider the out-of-plane shear.

Several failure criteria require additional parameters to be set. For example, Tsai-Wu uses F12 (OptiStruct, Nastran), which is read from the material card and treated as 0 if undefined.
Table 1.
Failure Criterion Parameter
Tsai-Wu F12 (OptiStruct, Nastran), f* (Abaqus)
Puck-CF (carbon fiber) Slope parameters:

p T I I + MathType@MTEF@5@5@+= feaahGart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8 qacaWGWbWdamaaBaaaleaapeGaamivaiaadMeacaWGjbGaey4kaSca paqabaaaaa@3ABD@ =0.35, p T I I − MathType@MTEF@5@5@+= feaahGart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8 qacaWGWbWdamaaBaaaleaapeGaamivaiaadMeacaWGjbGaeyOeI0ca paqabaaaaa@3AC8@ =0.3, p T I I − MathType@MTEF@5@5@+= feaahGart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8 qacaWGWbWdamaaBaaaleaapeGaamivaiaadMeacaWGjbGaeyOeI0ca paqabaaaaa@3AC8@ =0.275

Degradation parameters:

s=0.5, M=0.5
Puck-GF (glass fiber) Slope parameters:

p T I I + MathType@MTEF@5@5@+= feaahGart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8 qacaWGWbWdamaaBaaaleaapeGaamivaiaadMeacaWGjbGaey4kaSca paqabaaaaa@3ABD@ =0.30, p T I I − MathType@MTEF@5@5@+= feaahGart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8 qacaWGWbWdamaaBaaaleaapeGaamivaiaadMeacaWGjbGaeyOeI0ca paqabaaaaa@3AC8@ =0.25, p T I I − MathType@MTEF@5@5@+= feaahGart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8 qacaWGWbWdamaaBaaaleaapeGaamivaiaadMeacaWGjbGaeyOeI0ca paqabaaaaa@3AC8@ =0.2225

Degradation parameters:

s=0.5, M=0.5
LaRC alpha=53°

Terminology

Failure Index is the value of the failure function at the given load.

Reserve Factor/Factor of Safety is a measure of margin to the onset of failure. The effective load multiplied with the Reserve Factor gives the design margin. Thus, Reserve Factor values greater than one indicate a positive design margin and values less than one indicate a negative design margin. The values of Reserve Factors are always greater than zero.

Inverse Reserve factor = 1 / Reserve Factor

For linear criteria (max strain, max stress and max fiber stress), it is equal to the value of the failure function f. For other failure criteria, there are either closed form solutions or iterative procedures to calculate the Reserve Factor from the Failure Index and the Inverse Reserve Factor, respectively. If the load factor has been increased by 2e32 in iterative solving or the Failure Index is below 1e-32, then the Inverse Reserve Factor is set to 0, which corresponds to reserve factor being infinite.

Margin of Safety = Reserve Factor – 1.

As opposed to the Factor of Safety as the margin to be reported, you can also use safety factors to adjust the effective load used in the margin calculation while accounting for influences of statistical load distributions, allowables, or other design aspects. Two options are exposed in the First Ply Failure method.

Design Safety Factor is multiplied with the applied load Fapplied to get the effective load Feff.

Feff = Design Safety Factor * Fapplied

Stability Factor is used in addition to Design Safety Factor to account for the fact that many stability problems are modeled based on ideal structures while they are not geometrically perfect in reality. Hence, for stability related analyses (for example, wrinkling):

Feff = Stability Factor * Design Safety Factor * Fapplied

Both factors are utilized in load response failure and strength analysis. For strength analysis, this means that the critical loads shown are the applied loads that lead to onset of failure with given safety factors in effect.

Activate Failure Theories

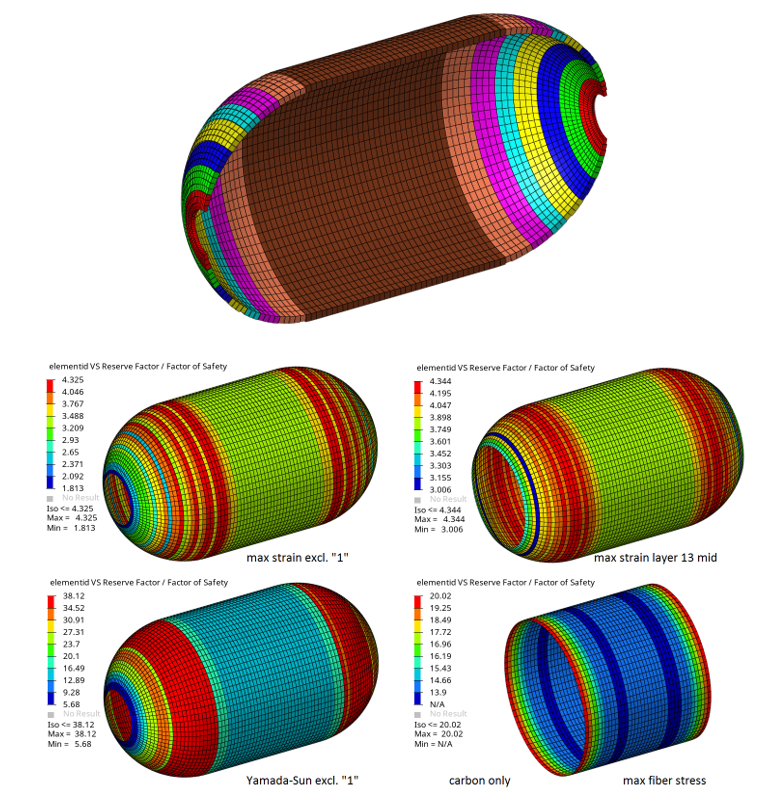
Once the First_Ply_Failure method is added to a designpointset, you can edit it from the browser. First, you can select the result level (Element | Layer | Recovery plane), then the type of margin to evaluate.

The failure theories that are available are grouped in categories in the Entity Editor, as per the description in Figure 1. You will activate methods of interest by providing materials to use for failure evaluation (Figure 2). As listed in Figure 1, all failure theories require allowable to be set directly in the referred material entities. Whenever these allowables are meant to be available directly as a solver card (MAT1/MAT8 attributes, or MATF for MAT1/MAT8/MAT9OR), they will be queried from the material card. Additional allowables or properties, not available from the solver deck, are automatically created as metadata attached to referenced material entity in HyperMesh. Metadata can be edited in each material Entity Editor. If a metadata already exists, it will not be overridden. Metadata is stored in the HyperMesh binary file along with the model.
Figure 2. First Ply Failure Selection and Allowable as Metadata


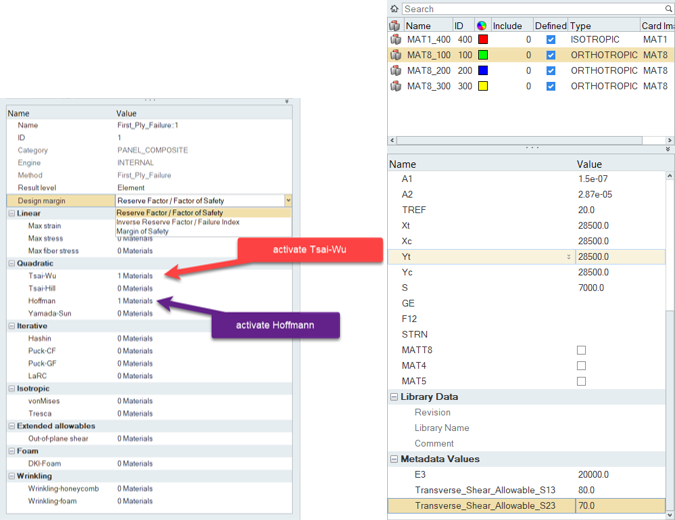
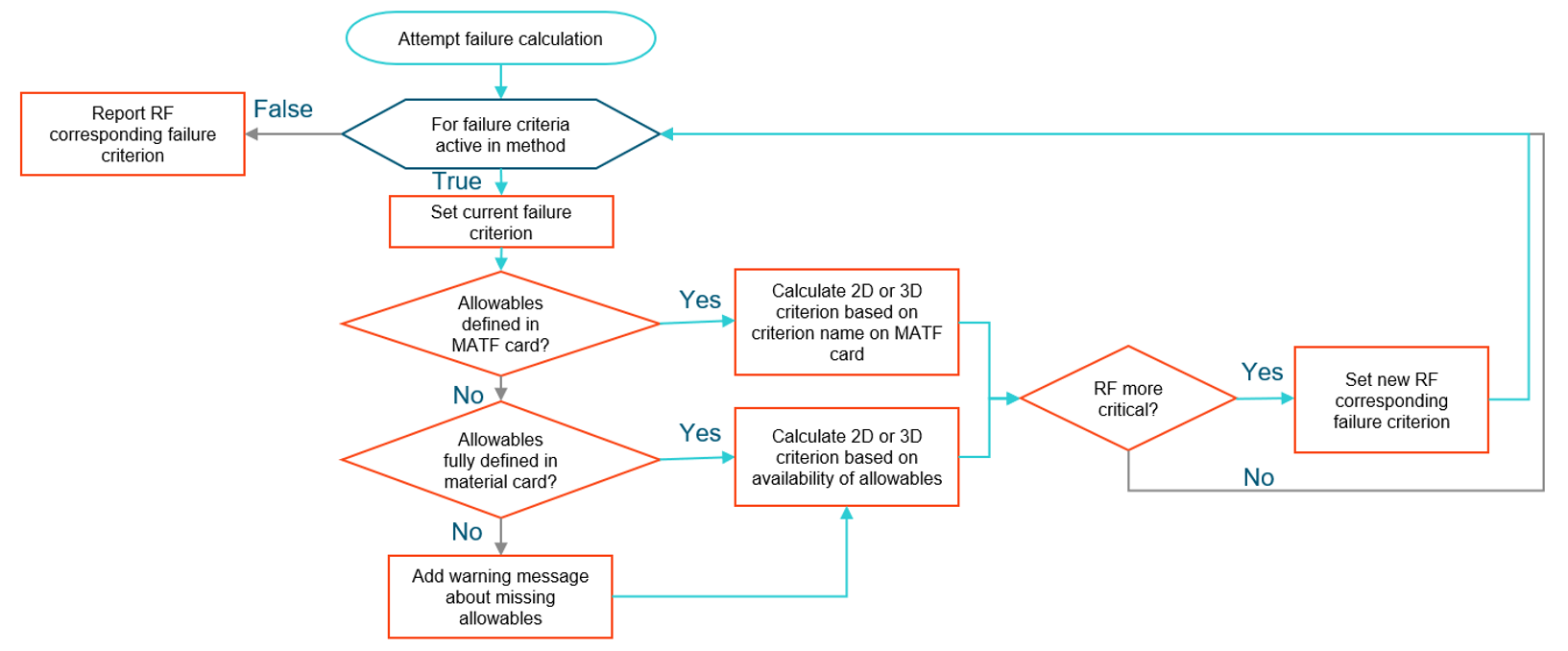
Multiple selections and combinations of failure criteria requiring different allowables are supported. The logic is outlined in Figure 3.

Figure 3. Design Margin Calculation Logic


The following OptiStruct MATF failure criteria are supported for reading:
  • 2D: PUCK, HILL, HOFF, TSAI, HASH, STRN, STRS
  • 3D: PUCK3D, HILL3D, HOFF3D, TSAI3D, HASH3D, STRN3D, STRS3D
Internally, 3D criteria are applied when possible, but stress in material normal direction is set to 0 due to the nature of the underlying first order shear deformation theory. Current limitations also include:
  • MATF PUCK3D, TSAI3D, and HASH3 failure criteria supports reading the allowables only, but not the additional parameters (W1, W2, W3). Standard set for those parameters for glass fiber and carbon fiber is used as per the ESAComp documentation for PUCK. F12 is used for TSAI3D. W1=alpha=1 is used for HASH3D.

Example 1: Local Post-Processing

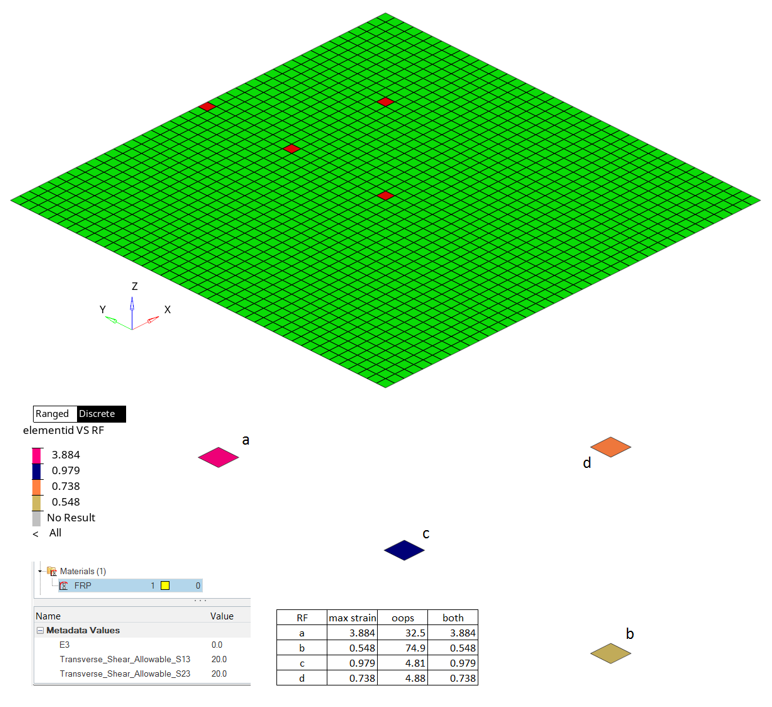
A corner supported uniformly pressure-loaded thick cross-ply laminated plate [13]. This tutorial highlights post-processing for four specific elements using two design criteria, namely Max strain and Out-of-plane shear. The latter requires additional strength allowable in the out-of-plane shear direction, which are introduced as HyperMesh metadata.
Figure 4.


Example 2: Global Post-Processing

Filament wound Composite Pressure Vessel (CPV) loaded with internal pressure. The CPV is wound from seven helical GFRP layer pairs and one circumferential CFRP layer pair. FPF results for the CPV are presented in the element level and layer level using Max strain criterion. For comparison, Yamada-Sun criterion-based results are presented in the element level. Finally, post-processing is performed only for the CFRP material using Max fiber stress criterion.
Figure 5.


First Ply Method References

  1. Mechanics of Composite Materials, Jones, R.M., Hemisphere, New York, 1975.
  2. Improved transverse shear stresses in composite finite elements based on first order shear deformation theory, R. Rolfes, K. Rohwer, International Journal for Numerical Methods in Engineering, 40:51–60, 1997.
  3. Failure criteria for an individual layer of a fiber reinforced composite laminate under in-plane loading. ESDU 83014, Amendment A. Engineering Sciences Data Unit, London, 1983/1986.
  4. Structural Materials Handbook, Volume 1 - Polymer Composites. ESA PSS-03-203, Issue 1. ESA Publications Division, ESTEC, Noordwijk, 1994.
  5. Introduction to Composite Materials. Technomic, Tsai, S.W. and Hahn, H.T., Westport, CT, 1980.
  6. Theory of Composite Design, Think Composites, Tsai, S.W., Dayton, OH, 1992.
  7. A Study of Failure Criteria of Fibrous Composite Materials, Paris F., George Washington University, Langley Research Center, Hampton, Virginia, NASA/CR-2001-210661.
  8. Failure Criteria for Unidirectional Fiber Composites, Hashin, Z., Journal of Applied Mechanics, 47 (1980), pp. 329-334.
  9. Failure criteria for non-metallic materials, Implementation of Puck´s failure criterion in ESAComp, FAIL-HPS-TN-003, European Agency Contract Report No. 16162/02/NL/CP, Braunschweig, 2004.
  10. Progressive failure analysis of advanced composites, Camanho P., NASA FA8655-06-1-3072, June 2009.
  11. Advanced Material Models for the Creep Behaviour of Polymer Hard Foams; Latest Advancements of Applied Composite Technology, Roth, M. A., Kraatz, A., Moneke, M., Kolupaev, V., Proceedings 2006 of the SAMPE Europe, 27th International Conference, Paris EXPO, Porte de Versailles, Paris, France, 27th - 29th March 2006. ISBN 3-99522677-2-4. pp. 253 - 2258.
  12. Manual for Structural Stability Analysis of Sandwich Plates and Shells, Sullins, R.T. et al, NASA CR-1457. 1969.
  13. A higher-order plate element for accurate prediction of interlaminar stresses in laminated composite plates, Ramesh S.S., Wang C.M., Reddy J.N. and Ang K.K., Composite Structures 91 (2009) 337–357.