Isotropic soft magnetic material: hysteresis Jiles-Atherton model
Introduction
In Flux, materials described by Jiles-Atherton model enable to take hysteresis phenomena into account during the solving process, as it is for Preisach models. This allows having a better accuracy, especially for the computation of the iron losses which can be evaluated by a direct computation, i.e. by a so-called a priori approach. Typical applications for hysteresis models are linear actuators, actuators with small airgap, torus etc.
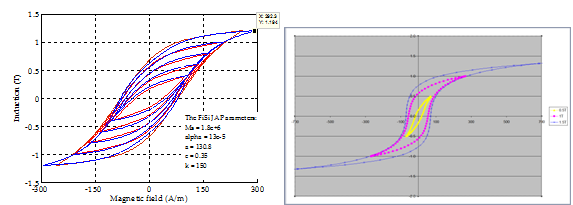
Jiles-Atherton hysteresis model in Flux
The model used in Flux is an isotropic, vector and static Jiles-Atherton (J-A) model.
It is defined by five parameters entered by user. The parameters are presented in the table below.
The model is available in Transient Magnetic application in 2D and 3D.
| Parameter | Physical property |
|---|---|
| Msat | Saturation magnetization |
| a | Shape parameter for anhysteretic magnetization |
| k | Pinning coefficient |
| c | Reversible wall motion coefficient |
| α | Mean field parameter representing inter-domain coupling |
Table 1. The five parameters of Jiles-Atherton model
Pros and cons of J-A model
The advantage of using vector model, comparing with a scalar model, is that it is possible to study applications with rotating magnetic flux.
The advantage of J-A model is that it is defined by only five parameters. Plus, the parameters are physical parameters of the material (in contrary to Preisach model, based on mathematical description).
On the other hand, J-A model presents sometimes some difficulties to reach the convergence and the modelling of minor loops is less accurate than Preisach models.
References
The model implemented in Flux was built by Johan Gyselinck and Ruth V. Sabariego. For more technical details on the model, please consult the following two articles:
- J. Gyselinck, P. Dular, N. Sadowski, J. Leite and J.P.A. Bastos, “Incorporation of a Jiles-Atherton vector hysteresis model in 2D FE magnetic field computations – Application of the Newton-Raphson method”, COMPEL, vol. 23, no. 3, pp. 685–693, 2004.
- J. Gyselinck, L. Vandevelde, J. Melkebeek and P. Dular, “Complementary two-dimensional finite element formulations with inclusion of a vectorized Jiles-Atherton model”, COMPEL, vol. 23, no. 4, pp. 959–967, 2004.