Models approximation in Steady state AC Magnetic applications

Reminder of Steady state AC Magnetic application

In Flux, in a Steady state AC Magnetic application, the unknown state variables and the derived physical quantities magnetic field strength and magnetic flux density are supposed to be harmonic (sinusoidal) time dependent.

The complex representation is used, and the solution can be obtained in a single solving process.

Problem raised

In a Steady state AC Magnetic application the state variable has sinusoidal time dependence, as well as the derived quantities magnetic field H and magnetic flux density B.

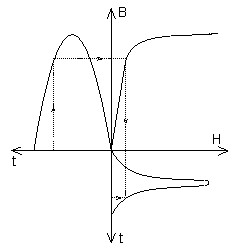
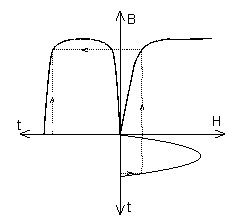
Or, in reality, if the field computation domain includes nonlinear magnetic materials, the magnetic field H and the magnetic induction H cannot have sinusoidal time dependence simultaneously (see figure below).


If B sinusoid …	If H sinusoid …

… ⇒ H non-sinusoid	… ⇒ B non-sinusoid

Proposed solution

To take into consideration the previously stated contradictions, approximations are carried out in the proposed models of magnetization.

The computation B(H) dependence is modified with respect to the proposed model for nonlinear magnetization based on the equivalence of magnetic energy. We then speak of an equivalent B(H) characteristic based on the energetic equivalence method.

Theory behind the method

The energy corresponds to the shaded surface in the figure below.

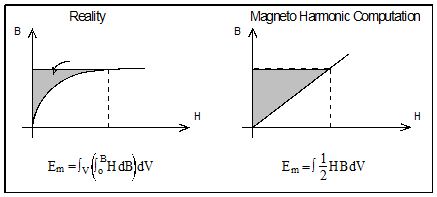
The equivalent B(H) dependence for Steady state AC Magnetic computations is calculated in such a way that the density of the time average magnetic energy per period of magnetic field time variation obtained starting from the real B(H) curve should be equal to the density of the magnetic energy given by the equivalent B(H) dependence.

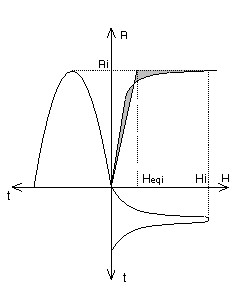
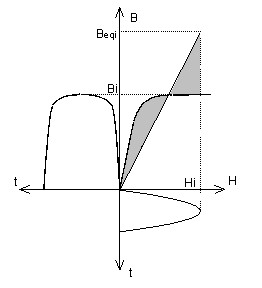
For the computation of the equivalent B(H) dependence, there are two extreme cases presented in the figure below.


B sinusoid	H sinusoid

Real magnetic state (B_i , H_i ): for B = B_i we get H = H_i The equivalent value H_eqi is obtained by horizontal displacement from the point (H_i, B_i ) in order to work at equivalent energy: for B = B_i we then get H = H_eqi The quantity H_eqi is calculated in such a manner as to have equality of the shaded surfaces.	Real magnetic state (H_i, B_i ): for H = H_i we get B = B_i The equivalent value B_eqi is obtained by vertical displacement from point (H_i, B_i) in order to work at equivalent energy: for H = H_i we then get B = B_eqi The quantity B_eqi is calculated in such a manner as to have equality of the shaded surfaces.

Theory behind the method (continued)

In reality, neither B nor H is sinusoidal. The results obtained with the equivalent curves calculated in the two extreme cases most often include the exact result. That is why the equivalent curve can equally be calculated by means of a linear combination between these two extreme cases (see the equivalent models provided in Flux).

Equivalent curves

The equivalent curves are presented in the figure below.

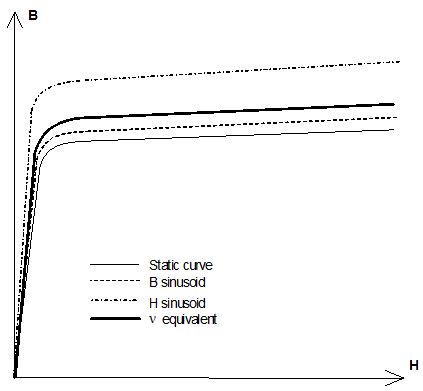
Limits of the method

In all cases, only the numerical values of the post-processed quantities that depend on the energy are correct (force, power, inductance, etc.).

Regarding the instantaneous quantities, they are approximations, since they are expressed in a sinusoidal shape. Still, they can give a more or less precise idea of the results.

Bibliography

Complementary information on the modeling of nonlinear magnetic materials in Steady state AC Magnetic is available in the following documents:

“Contribution à la modélisation des moteurs asynchrones par la méthode des éléments finis”thesis of Eric VASSENT – 1990INPG (Contribution to the modelling of asynchronous motors by the finite elements method)
“Détermination des pertes par courant de Foucault dans les cuves de transformateursModélisation de régions minces et prise en compte de la saturation des matériaux magnétiques en régime harmonique”thesis of Christophe GUERIN – 1994INPG (Determining of eddy current losses in the transformers curves – Modeling of narrow regions and taking into consideration of magnetic materials in harmonic regime)
“Simulation of induction machine operation using complex magnetodynamic finite elements” by Eric VASSENT – IEEE Transactions on magnetics, vol. 25, No 4, July 1989

Flux models

The models provided in Flux for the B(H) equivalent dependencies are presented in the following table.


Model	Hypothesis	Equivalent B(H) curve
Non-modified curve		Real B(H)
Sinusoidal induction	B sinusoid B = B_msinωt	This model is based on the following energetic equivalence: This model is more adapted for the simulation of devices with a voltage supply.
Sinusoidal H field	H sinusoid H = H_msinωt	This model is based on the following energetic equivalence: This model is more adapted for the simulation of devices with a current supply.
Mixed		This model is the linear combination of the two preceding ones: B_eq = α.B_eqBsin +(1- α)B_eqHsin H_eq = α.H_eqBsin +(1- α)H_eqHsin where α is a weighting coefficient chosen empirically in the interval 0, 1
Average of ν over a period	B sinusoid B = B_msinωt	This model relies on an equivalent reluctivity ν_eq calculated by getting the average of reluctivity over a period of time: It is much less precise than the others for high values of magnetic flux density, as it does not observe the asymptote of µ₀ slope.