Hysteretic Spring Model

The Hysteretic Spring contact model allows plastic deformation behaviors to be included in the contact mechanics equations, resulting in particles behaving in an elastic manner up to a predefined stress.

Once this stress is exceeded, the particles behave as though undergoing plastic deformation. The result is that large overlaps are achievable without excessive forces acting upon them, thus representing a compressible material. Hysteretic Spring normal force calculation is based on the Walton-Braun theory described in the works of Walton and Braun (Walton and Braun 1986), (Walton and Braun 1986).

The following figure describes the Hysteretic Spring contact model force displacement relationship.

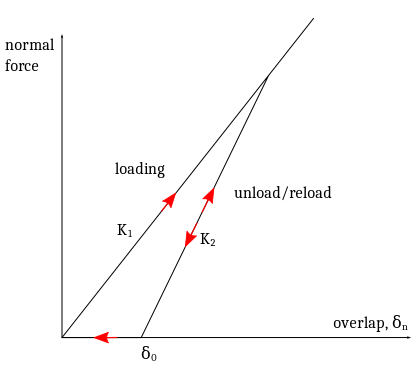
Note: The unloading force goes to zero before the displacement recovers to the initial contacting point.

The quantity δ₀ represents the residual ‘overlap’ that remains because of the plastic deformation - flattening in the contact region. The exact location of each old contact spot is not ‘remembered,’ so that particles become like new undeformed spheres once they separate. Subsequent contacts will load along a new loading path with slope, K₁. Any reloading before separation follows the slope K₂ until the original loading curve K1 is reached, whereupon the lower slope is followed until unloading occurs.

The normal force, F_N, is defined as:

$F_{n} = - \{\begin{array}{l} K_{1} δ_{n} f o r l o a d i n g (K_{1} δ_{N} < K_{2} (δ_{n} - δ_{0})) \\ K_{2} (δ_{n} - δ_{0}) f o r u n l o a d i n g / r e l o a d i n g (δ_{n} > δ_{0}) \\ 0 f o r u n l o a d i n g (δ_{n} \leq δ_{0}) \end{array}\}$

Where K₁ and K₂ are the loading and unloading stiffness respectively, δ_n, is the normal overlap and δ₀ is the residual overlap. Loading stiffness, K₁, is related to the yield strength of each material participating in contact, Y₁ and Y₂, as follows (Walton O., 2006) in:

$K_{1} = 5 R^{*} \min (Y_{1}, Y_{2})$

Here, R^* is the equivalent radius of the two particles participating in the contact. The Coefficient of Restitution is defined as:

$e = \sqrt{\frac{K_{1}}{K_{2}}}$

This allows for the determination of K>₂ from K₁ (Walton O. , 2006). Residual overlap is updated every Time Step according to the following rule:

$δ_{n} = - \{\begin{array}{l} δ_{n} (1 - \frac{K_{1}}{K_{2}}) f o r l o a d i n g (K_{1} δ_{N} < K_{2} (δ_{n} - δ_{0})) \\ δ_{0} f o r u n l o a d i n g / r e l o a d i n g (δ_{n} > δ_{0}) \\ δ_{n} f o r u n l o a d i n g (δ_{n} \leq δ_{0}) \end{array}\}$

The main energy dissipation mechanism is due to the difference in spring stiffness between loading and unloading phases. The need for an additional velocity dependent dissipation mechanism, to suppress possible undamped low amplitude oscillations, was suggested in (Walton O. , 2006). In EDEM's Hysteretic Spring model, this mechanism was implemented in a way similar to the linear spring normal damping force scaled by a dimensionless user set parameter Damping Factor, b_n, as follows:

$F_{n}^{d} = - b_{n} \sqrt{\frac{4 m^{*} k}{1 + {(\frac{π}{\ln e})}^{2}}} v \vec{_{n}^{r e l}}$

Here k is either K₁ or K₂. The rest of the variables and factors in the above expression are explained in the Linear Spring contact model section.

Since the Hysteretic Spring model for normal force can be considered as an extension of the Linear Spring model for normal force, it is recommended to use tangential components of the Linear Spring model for tangential forces. In particular, a more general form of the Linear Spring Elastic tangential force is used in the Hysteretic Spring model in which the force depends on the user-defined stiffness factor, γ_t, as follows:

$F_{t} = - \min (γ_{1} K_{1} δ_{t} + F_{t}^{d}, μ F_{n})$

As opposed to the normal component, the tangential damping force is not scaled by the damping factor.

$F_{t}^{d} = - \sqrt{\frac{4 m^{*} γ_{t} k}{1 + {(\frac{π}{\ln e})}^{2}}} v \vec{_{t}^{r e l}}$

For particles, a default value for the Yield Strength is estimated from the Young’s Modulus E and Radius of the particle R according to the algorithm suggested in (Walton O. , 2006). Initially, the possible default value is calculated as follows:

$Y = \frac{4}{15} \frac{E}{\sqrt{R}} \frac{1}{70}$

If this value is less than 100Pa, it is replaced with a value of 0.003 *E.

For Geometries, the default value is set to 1e+09 Pa.

The following table describes the interaction and contact model parameters for the Hysteretic Spring model.


Interaction	Configurable Parameters	Position
Particle-Particle, Particle-Geometry	Click the + icon to add Particle-Particle or Particle-Geometry interactions. Set the following interaction parameters: Damping factor This dimensionless parameter controls the amount of velocity dependent damping. Without this additional damping, small vibrations of particles can persist for a long time. Setting this parameter to zero suppresses only the velocity-dependent damping without affecting the main energy loss mechanism due to the nature of the linearized elasto-plastic model. The recommended value for this parameter is zero when modeling “aggressive” compression of materials and small non-zero value for small stain compression regimes. Stiffness factor This dimensionless parameter is defined as the ratio of tangential stiffness to normal loading stiffness and used in calculation of tangential forces at the contact. According to the literature, the typical value of this parameter is in the range between 0.7 and 1. Also set the yield strength in units of Pa for each particle or Geometry that has an interaction. EDEM offers a reasonable default value for this parameter estimated from material Shear Modulus. You can, however, overwrite this default value.	Last