Hertz-Mindlin with JKR Model

The Hertz-Mindlin with JKR contact model works within the contact zone and allows you to model strongly adhesive systems, such as dry powders or wet materials.

Hertz-Mindlin with JKR (Johnson-Kendall-Roberts) Cohesion is a cohesion contact model that accounts for the influence of Van der Waals forces. In this model, the implementation of normal elastic contact force is based on the Johnson-Kendall-Roberts theory (Johnson, Kendal and Roberts 1971).

Hertz-Mindlin with JKR Cohesion uses the same calculations as the Hertz-Mindlin (no slip) contact model for the following types of forces:

Tangential elastic force
Normal dissipation force
Tangential dissipation force

JKR normal force depends on the overlap δ and the interaction parameter, surface energy γ as follows:

$F_{J K R} = - 4 \sqrt{π γ E *} a^{3 / 2} + \frac{4 E^{*}}{3 R^{*}} a^{3}$

$δ = \frac{a^{2}}{R^{*}} - \sqrt{\frac{4 π γ α}{E^{*}}}$

Here, E^* is the equivalent Young’s modulus, and R^* is the equivalent radius defined in the Hertz-Mindlin (no slip) Model section.

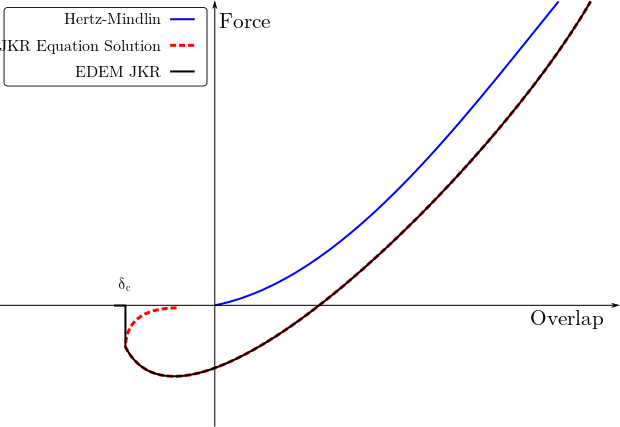
The normal force is a function of normal overlap. The Hertz-Mindlin with JKR cohesion model results are compared with the Hertz-Mindlin (no slip) model results. Negative overlap is the gap between two separated particles.

The EDEM JKR normal force follows the same solution of the above equations for both loading and unloading phases. The figure shows the typical plot of JKR normal force as a function of normal overlap.

For γ = 0, force turns into Hertz-Mindlin normal force:

$F_{H e r t z} = \frac{4}{3} E^{*} \sqrt{R^{*}} δ^{^{\frac{3}{2}}}$

This model provides attractive cohesion forces even if the particles are not in physical contact. The maximum gap between particles with non-zero force is defined as:

$δ_{c} = - \sqrt{\frac{4 π γ a_{c}}{E^{*}}} + \frac{a_{c}^{2}}{R^{*}}$

$a_{c} = {[\frac{9 π γ R^{* 2}}{2 E^{*}} (\frac{3}{4} - \frac{1}{\sqrt{2}})]}^{^{\frac{1}{3}}}$

For δ < δ_c , the model returns zero force. The maximum value of the cohesion force occurs when particles are not in physical contact and the separation gap is less than δ_c. The value of maximum cohesion force, called pull-out force, is defined as:

$F_{p u l l o u t} = - \frac{3}{2} π γ R^{*}$

Friction force calculation is different from the Hertz-Mindlin (no slip) model. In that, it depends on the positive repulsive part of JKR normal force. As a result, the EDEM JKR Friction model provides greater friction force when the cohesion component of the contact force is higher. The importance and advantages of this Friction Force model correction in the presence of strong cohesive forces was noted and illustrated in (Baran, et al. 2009), (Gilabert, Roux and Castellanos 2007).

Although this model was designed for fine, dry particles, it can be used to model wet particles. The force needed to separate two particles depends on the liquid surface tension γ_c and the wetting angle θ:

$F_{p u l l o u t} = 2 π γ_{s} \cos (θ) \sqrt{R_{i} R_{j}}$

Equating the above force to JKR max force allows JKR surface energy parameter estimation if the EDEM particle size is not scaled.


Interaction	Configurable Parameters	Position
Particle to Particle, Particle to Geometry.	Click + to add cohesion to particle-particle or particle-geometry interactions. Set the surface energy for each interaction. Surface energy is a property of the materials ability to retain moisture/charge on its surface. The amount of surface energy influences the adhesion of the material. The SI units of surface energy are J/m^².	Last

In the Creator Tree, select Physics.
Select the required interaction from the Interaction dropdown list.
Click the + icon and then select Hertz-Mindlin with JKR Cohesion.
Click the icon to define the contact model parameters.

Note: It is not recommended to use this contact model with particle contact radius 'ON' since this will result in an attractive force before a physical contact is made (see the Hertz-Mindlin with JKR Version 2 model).