Nonlinear Spring Mass Damper System
Consider a mass-spring-damper system, with nonlinear stiffness and damping.
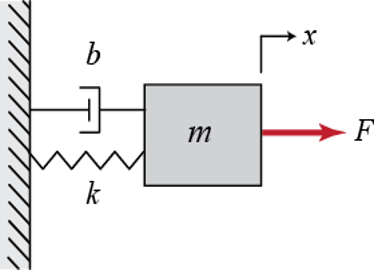
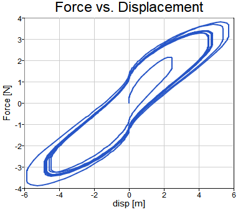
The nonlinear formulation of stiffness and damping is unknown. Nevertheless, the goal is to obtain a romAI model capable of predicting the spring-damper force and the mass position along time, given the external force and arbitrary initial conditions for the mass.
As typical for mechanical systems, mass position and velocity are the system state variables.
Hence, the romAI model can be schematized by the following block diagram.
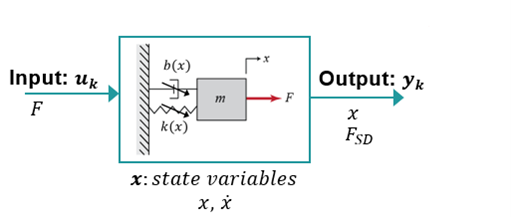
In order to train the romAI model, time histories of inputs, outputs, and state variables are needed.
In this case, the training dataset consists of three separate time histories. Each time history has been built by exciting the system with a different external force over time. The three external exciting forces are plotted here.
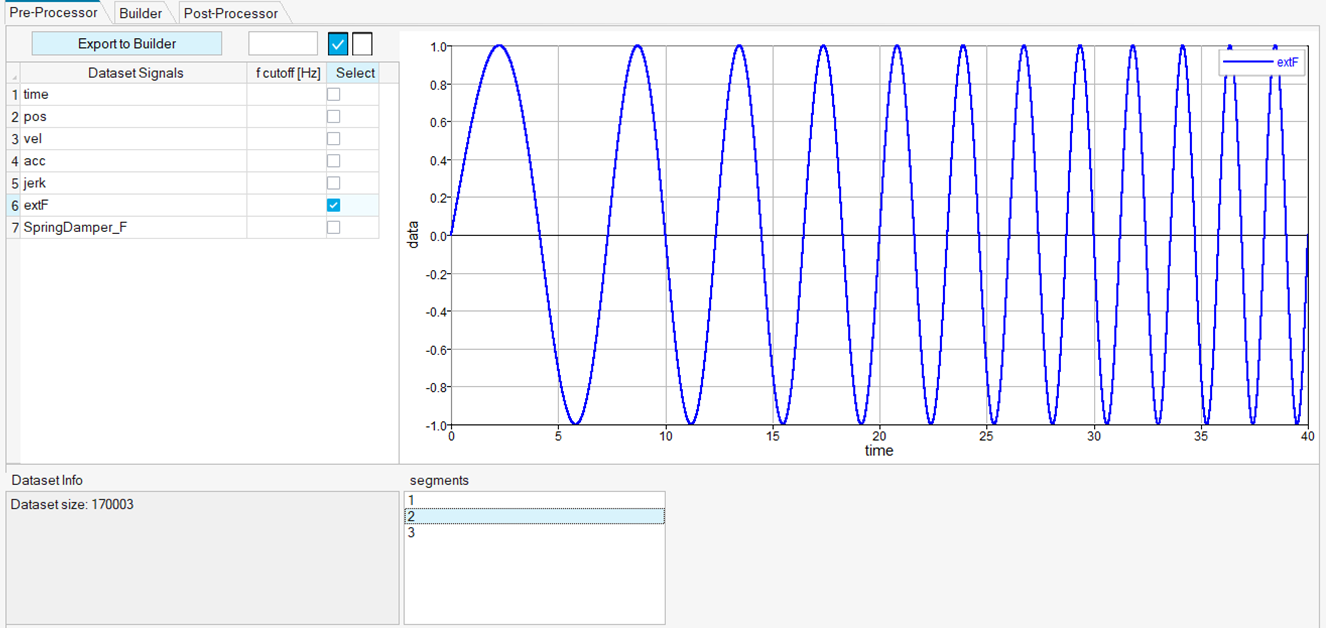
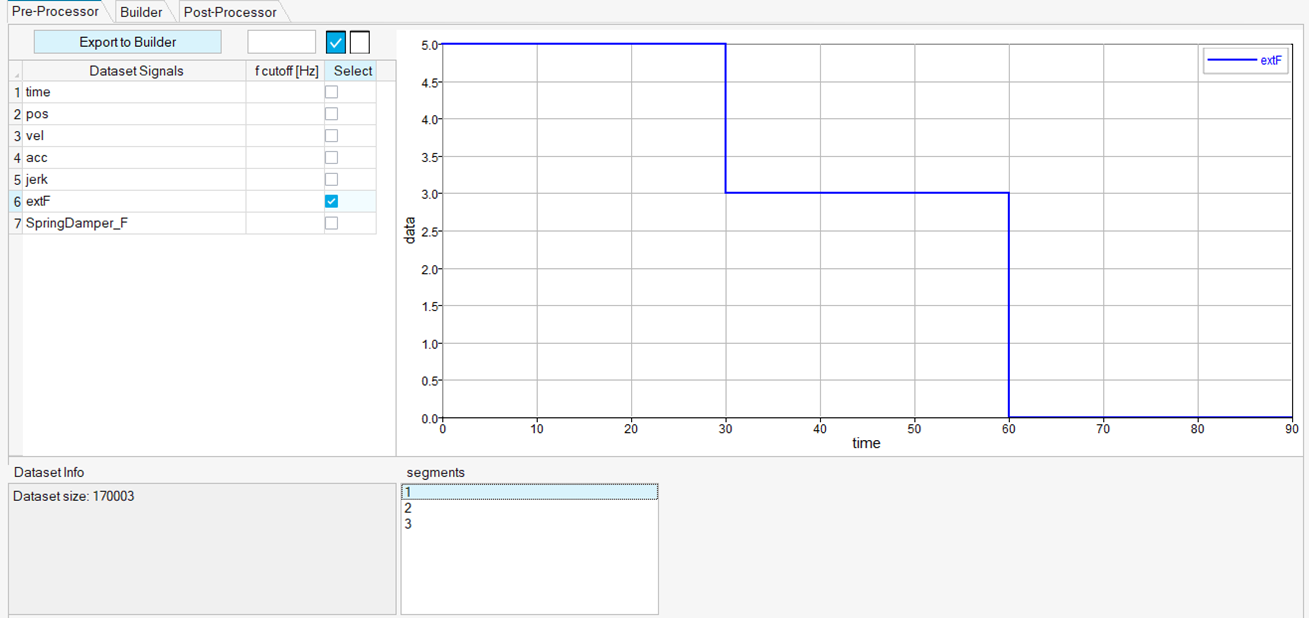

The external exciting forces are chosen as typical exiting forces in system identification practice. Different levels of external force amplitude are spanned to account for system nonlinearities.
Given the dataset, the romAI model can be built easily through the Builder tab.
- Specify the model path and name.

- Specify the Inputs, Outputs, and States.
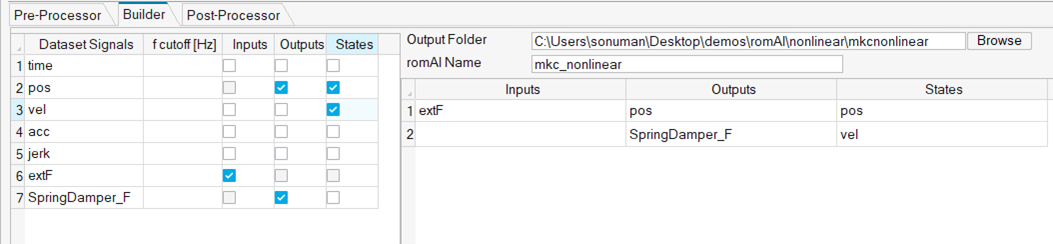
- Define the physical constraints (i.e., mass velocity is the derivative of mass
position).

- Define the model Settings:
- Model Type: non linear
- (Hidden) Activation Function: relu
- Hidden Layers: 3
- Neurons X (Hidden) Layer: [20,20,20]
- Epochs: 10
- Test Split Ratio: 0.2

- Set the Advanced Settings:
- Learning Rate: 1e-3
- Regularization Coefficient: 0

- Start the training procedure.
After the training has completed, the Loss vs Epochs curve is automatically displayed in the Post-Processor tab, together with all the romAI model information.

Further investigations regarding the accuracy of the romAI model can be carried over in the Post-Processor tab. Moreover, the romAI model can be deployed in Twin Activate using the built-in romAI block.
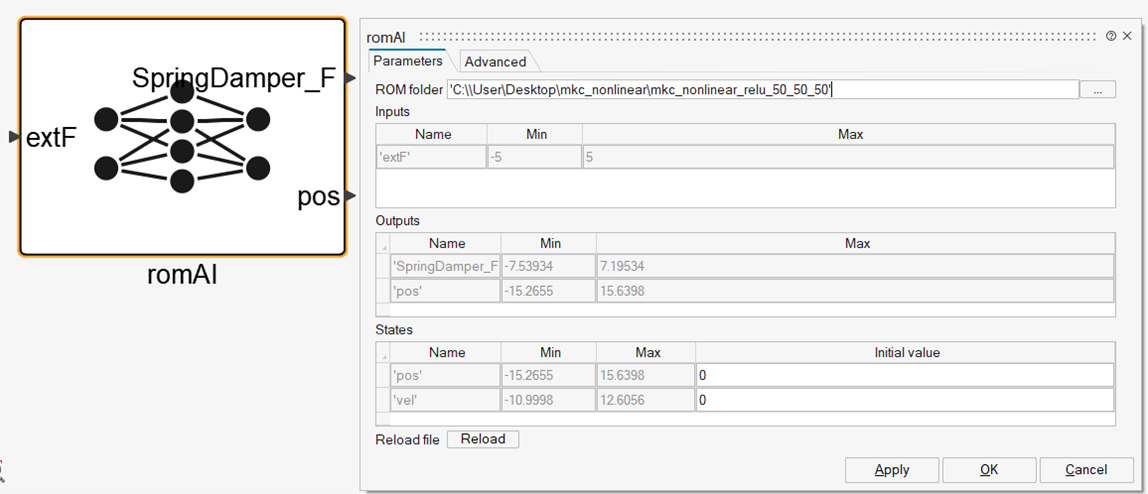
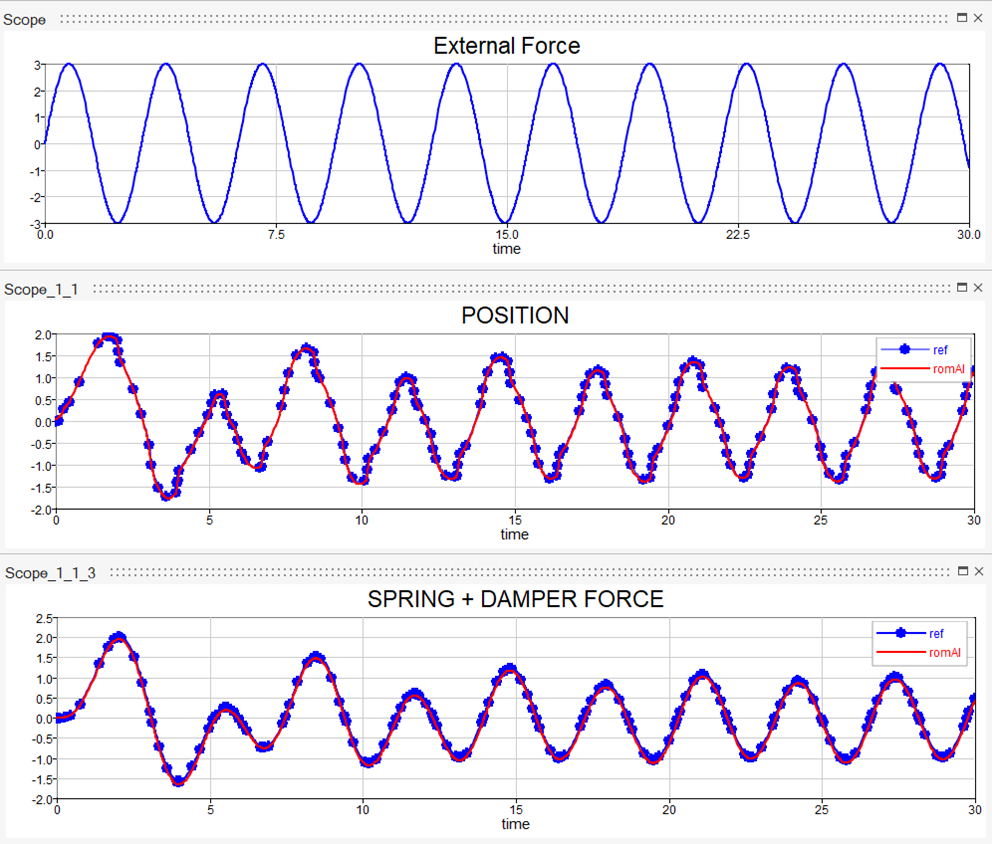
The results produced by the romAI model with respect to the reference mass-spring-damper system, given a sinewave as the external force, are shown here.