HS-1506: Material Calibration with a Curve Difference Integral
In this tutorial, you will learn how to register a Compose, Python, or Templex function in HyperStudy.
The .py and .oml file contain a function that calculates the area between two curves.
The objective of this tutorial is to find the Radioss material parameter values so that the stress-strain curve of the tensile test simulation matches the tensile test experimental curve.
HS-1507: Material Calibration with Area Tool in Data Source provides an alternative method to set up this problem using the Area tool.
HS-4200: Material Calibration Using System Identification provides an alternative method to set up this problem using system identification.
- Create an input template from a Radioss file using the HyperStudy - Editor
- Register a Compose, Python, or Templex function
- Set up a study
- Run a system identification optimization study
Model Definition
A quarter of a standard tensile test specimen is modeled using symmetry conditions. A traction is applied to a specimen via an imposed velocity at the left-end.



- Stress level
- Plastic strain
- Yield Stress
- Hardening modulus
- Hardening exponent
- Strain rate coefficient
- Strain rate
- Reference strain rate


Create Base Input Template
In this step, you can create the base input template in HyperStudy or use the base input template in the study Directory.
- Start HyperStudy.
-
From the menu bar, click .
The Editor opens.
- In the File field, open the TENSILE_TEST_0000.rad file.
-
In the Find area, enter /MAT/PLAS_JOHNS/1 and click
 .
HyperStudy highlights /MAT/PLAS_JOHNS/1.
.
HyperStudy highlights /MAT/PLAS_JOHNS/1.Figure 5. 
-
Select variable E by highlighting the first 20 fields in row 51.
Tip: Quickly highlight 20-character fields by pressing Ctrl to activate the Selector (set to 20 characters) and then clicking the value.
Figure 6. 
- Right-click on the highlighted fields and select Create Parameter from the context menu.
-
In the Parameter: varname_1 dialog, define the following
options and click OK.
- In the Label field, enter E_Young.
- Change the Lower Bound to 50000.
- Change the Nominal value to 60400.
- Change the Upper Bound to 70000.
- Change the Format to %20.5f.
Figure 7. 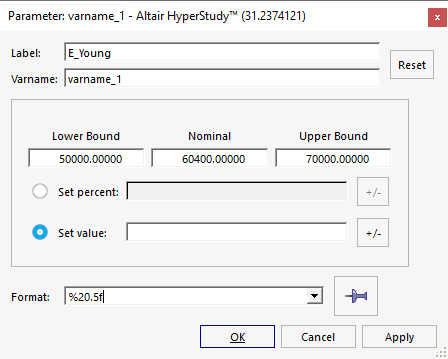
-
Define four more variables using the information provided in Table 1.
Table 1. Variable Label Lower Bound Nominal Upper Bound Format a a_PlasticityYieldStress 90 110 120 %20.5f b b_HardeningCoeff 100 125 160 %20.5f n n_HardeningExpo 0.1 0.2 0.3 %20.5f sigmax Sigma_Max 250 280 290 %20.5f - Click Save.
- In the Save Template dialog, save the file as TENSILE_TEST_0000.tpl.
- Close the Editor.
Register Curve Difference Function
In this step you will register the curve difference function using Compose/OML, Python, or Templex.
The function curve_difference calculates the integral of the
absolute value of the difference between two curves over the common domain of the
supplied functions. This is a robust function that tends to zero only as the two
functions become equal.
-
Register the
curve_differencefunction using Compose.- Start Compose.
- From the menu bar, click .
- In the Open File dialog, open the file Curve_Difference.oml.
-
Highlight the function
curve_difference(...). - Right-click on the highlighted text and select Register Function from the context menu.
- In the Register Function dialog, click OK.
- Close Compose.
-
Register the
curve_differencefunction using Python. -
Register the
curve_differencefunction using Templex.- From the menu bar, click .
- In the HyperStudy - Set Preference File dialog, open the curve_difference.mvw file.
Perform the Study Setup
-
Start a new study in the following ways:
- From the menu bar, click .
- On the ribbon, click
 .
.
- In the Add Study dialog, enter a study name, select a location for the study, and click OK.
- Go to the Define Models step.
-
Add a Parameterized File model.
-
Define a model dependency.
- Click Model Resources.
- In the Model Resource dialog, select Model 1 (m_1).
- Click .
- In the Select File dialog, navigate to your working directory and open the TENSILE_TEST_0001.rad file.
- Set Operation to Copy.
- Click Close.
Figure 9. 
-
Click Import Variables.
Five input variables are imported from the TENSILE_TEST_0000.tpl resource file.
- Go to the Define Input Variables step.
- Review the input variable's lower and upper bound ranges.
Perform Nominal Run
- Go to the Test Models step.
-
Click Run Definition.
An approaches/setup_1-def/ directory is created inside the study Directory. The approaches/setup_1-def/run__00001/m_1 directory contains the input file, which is the result of the nominal run.
Create and Evaluate Output Responses
In this step, you will use the curve_difference function to create
and evaluate output responses.
In order to fit the RADIOSS stress-strain curve to the experimental data, you must compare the two curves.
-
Create the Area Between Two Curves output response.
- Go to the step.
- Click Add Output Response.
- In the work area, Label field, enter Area Between Two Curves.
Figure 10. 
-
Create a data source labeled Disp_sim.
-
Create a second data source labeled Force_sim by
repeating step 2.
Define the following options:
- Set Type to Section/SECTION_2.
- Set Request to 2 section 1.
- Set Component to FT-Resultant Tangent Force.
-
Create a third data source labeled Strain_exp.
-
Create a fourth file source labeled Stress_exp by
repeating step 4.
Select the following options:
- Set Type to Unknown.
- Set Request to Block1.
- Set Component to Column 2.
-
Define the Area Between Two Curves output response.
- Click OK to close the Expression Builder.
- Click Evaluate to extract the response values.
Run Optimization
-
Add an Optimization.
- In the Explorer, right-click and select Add from the context menu.
- In the Add dialog, select Optimization.
- For Definition from, select Setup and click OK.
- Go to the step.
- Click the Objectives/Constraints - Goals tab.
-
Apply an objective on the Area Between Two Curves output response.
- Click Add Goal.
- In the Type column, select Minimize.
Figure 15. 
- Go to the step.
-
In the work area, set the Mode to Adaptive
Response Surface Method (ARSM).
Note: Only the methods that are valid for the problem formulation are enabled.
- Click Apply.
- Go to the Evaluate step.
- Click Evaluate Tasks.
-
Click the Evaluation Plot tab to plot the optimization
iteration history of the objective.
Figure 16. 




