Courbes 3D dédiées aux machines tournantes
Généralités
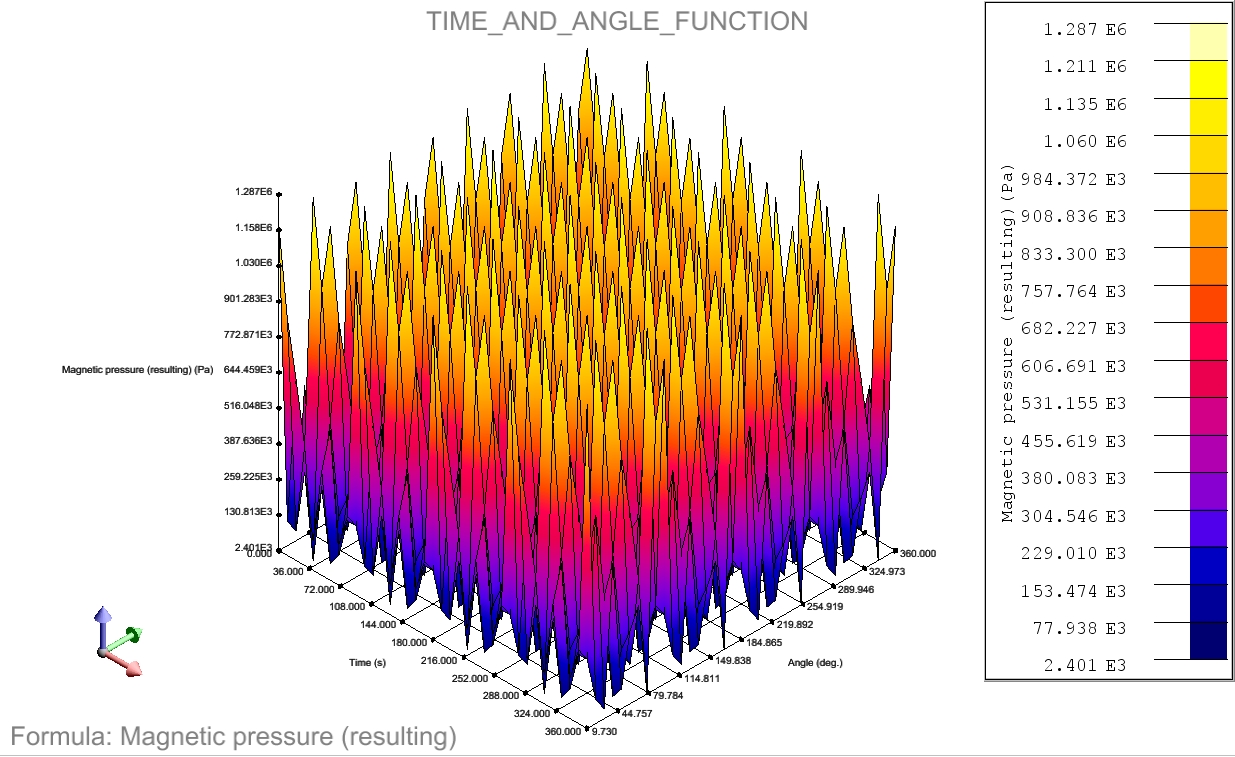
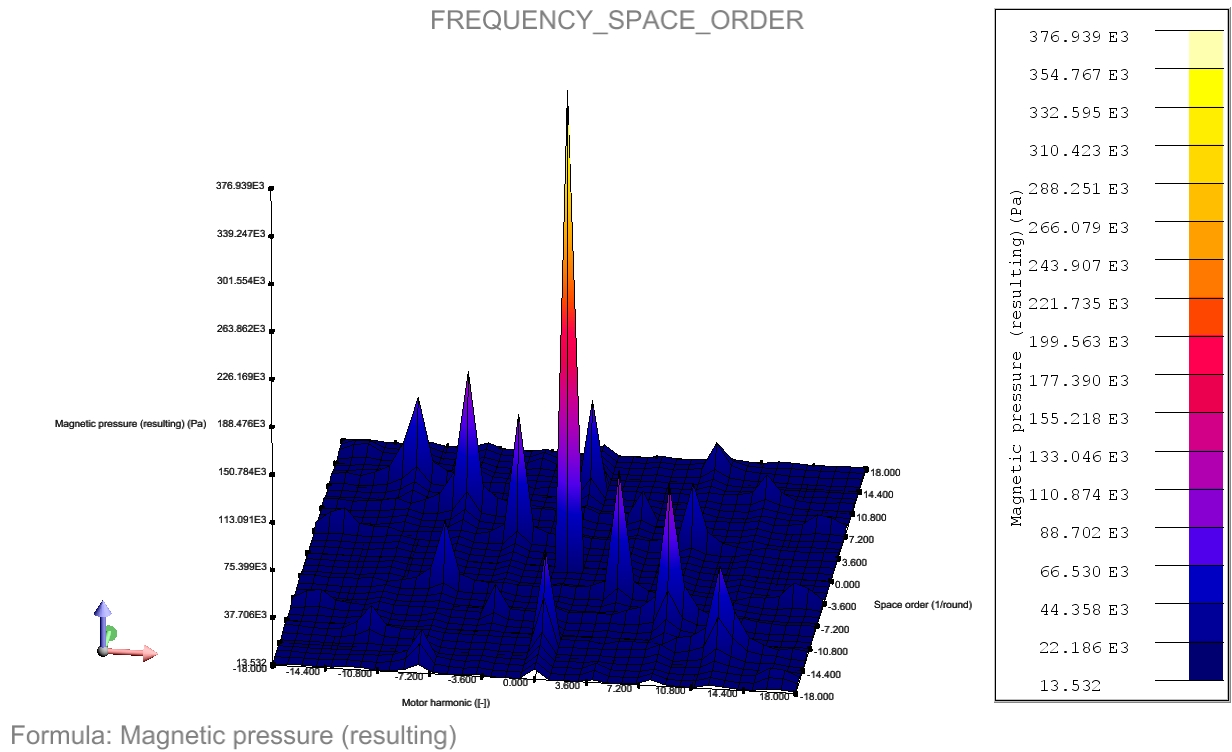
Les courbes 3D dédiées aux machines tournantes permettent de calculer les valeurs d’une formule le long d’un cercle de calcul disposé autour de l’axe de rotation d’une machine tournante, typiquement dans la zone d'entrefer. Ces valeurs sont collectées pour une série de pas de temps (fonctionnalité disponible uniquement en application Magnétique Transitoire). Une fois collectées, les valeurs sont présentées sous la forme d’une courbe 3D dont les abscisses sont le temps et la position angulaire le long du cercle de calcul. Une option spécifique permet aussi de transformer les valeurs temporelles dans une représentation dans un domaine de Fourier 2D, où les données sont exprimées en fonction de l’harmonique moteur et de l’ordre spatial.Options de la boîte de dialogue
La boite de dialogue pour la création d'une courbe 3D dédiée aux machines tournantes est présentée ci-dessous :
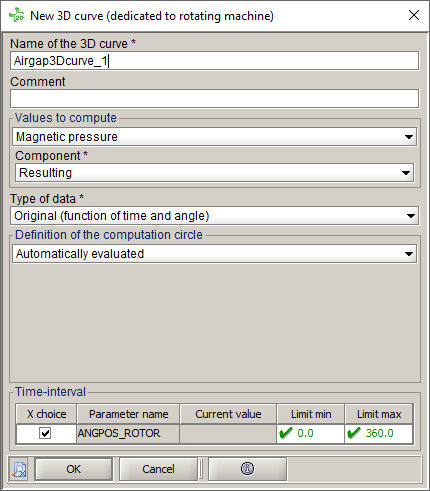
Les champs que l'utilisateur doit renseigner sont les suivants :
- Valeurs à calculer : l'utilisateur peut choisir entre :
la Pression magnétique, qui est la grandeur la plus utilisée dans cette analyse et qui permet de calculer le module de la pression magnétique ou, éventuellement, de se limiter à une de ses composantes : radiale (appelée aussi normale) ou tangentielle.
Cette pression magnétique aux points de calcul est obtenue par la formule :
où les premier et second termes représentent, respectivement, la composante normale et tangentielle de la pression magnétique.
- et sa propre Formule utilisateur, qui permet de calculer les valeurs d’une formule spatiale définie par l’utilisateur. La quantité exprimée par la formule choisie doit être scalaire réelle.
- Type de données : l'utilisateur peut choisir entre :
- Original (fonction du temps et de l'angle), qui retourne les valeurs dans le domaine temps/position angulaire.
- Double FFT (fonction de l'harmonique moteur et de l'ordre spatial), qui retourne les valeurs dans le domaine fréquence/ordre spatiale. Ces valeurs sont obtenues par l’application d’une transformée de Fourier 2D, les fréquences sont normalisées par la vitesse de rotation pour être exprimées en termes d’harmoniques moteur.
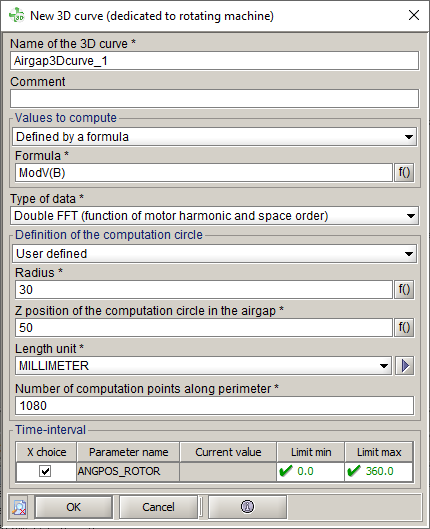
- Définition du cercle de calcul : en 2D et en Skew, Flux
propose par défaut l'évaluation automatique du cercle de calcul. L'utilisateur
peut néanmoins définir soi-même les paramètres en sélectionnant l'option définie
par l'utilisateur, qui est d'ailleurs la seule disponible en 3D. Dans le cas
de cette option définie par l'utilisateur, montrée dans l'image ci-dessous,
l'utilisateur est invité à définir :
- le Rayon du cercle où calculer la quantité choisie ;
- dans les applications Skew et 3D, la Position suivant Z du cercle de calcul dans l’entrefer ;
- l'Unité de longueur utilisée pour le rayon et pour la position suivant Z du cercle de calcul dans l'entrefer ;
- le Nombre de points de calcul sur le périmètre, dont la valeur par défaut est 1080, c'est-à-dire trois points par degré pour un tour complet de rotation.
- Intervalle temporel
- Intervalle, permet de sélectionner une série de pas de temps (ou de positions). Si le type de donnée Double FFT est sélectionné, l’intervalle doit représenter un tour complet du rotor autour de son axe afin d'assurer la périodicité de l'évolution temporelle.
Exemples de courbes 3D
