Rural Dominant Path Model

The Dominant Path Model uses a full 3D approach for the path searching, which leads to realistic and accurate results.

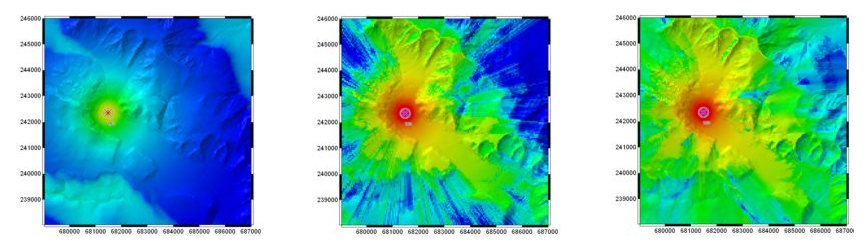
Ordinary rural or suburban wave propagation models are based on empirical approaches. They compute only the direct ray between transmitter and receiver location. This leads often to too pessimistic results, as these models are based on the assumption that most part of the energy is transmitted with the direct path. Depending on the scenario, for example, if the terrain is very hilly, this approach does not match the reality. The following picture shows a comparison between the results of the ordinary Hata-Okumura model, a knife-edge diffraction model and the dominant path model.

Figure 1. Comparison of results between the Hata-Okumura (on the left), knife-edge diffraction (middle) and dominant path models (to the right).

The simple approach of the Hata-Okumura Model is clearly visible in the left image. Topography between transmitter and receiver is not considered. In contrast to this case, the Knife-Edge Diffraction Model considers topography, but the effects are too dominant. The shadows behind the hills are too hard, because always the direct ray is considered. This leads to too pessimistic results. The Dominant Path Model uses a full 3D approach for the path searching, which leads to realistic and accurate results.

Advantages of the Dominant Path Model

As a consequence of the properties and restrictions of the available prediction models mentioned above, the dominant path prediction model (DPM) has been developed. The main characteristics of this model are as follows:

The most important propagation path is computed by using a full 3D approach
Short computation times
Accuracy exceeds the accuracy of empirical models

Algorithm of the Dominant Path Model

The DPM determines the dominant path between transmitter and each receiver pixel. The computation of the path loss is based on the following equation:

L = 20 \log (\frac{4 π}{λ}) + 10 p \log (l) + \sum_{i = 0}^{n} f (φ, i) - Ω - g_{t}

L is the path loss computed for a specific receiver location. The following parameters are considered by the model:

Distance from transmitter to receiver (l)
Path loss exponent (p)
Wave length (lambda)
Individual interaction losses due to diffractions (f)
Empirically determined loss reduction due to wave guiding ( $Ω$ )
Gain of transmitting antenna (g_t)

As described above, l is length of the path between transmitter and current receiver location. p is the path loss exponent. The value of p depends on the current propagation situation. In areas with vegetation (which is not modeled in the project) p = 2.4 is suggested, whereas in open areas p = 2.0 is reasonable. In addition p depends on the breakpoint distance. After the breakpoint, increased path loss exponents are common due to distortions of the propagating wave. The function f yields the loss (in dB) which is caused by diffractions. The diffraction losses are accumulated along one propagation path. The directional gain of the antenna (in direction of the propagation path) is also considered.

Configuration of the Dominant Path Model

The following screenshot shows the configuration dialog of the DPM.

Figure 2. The Configuration of Dominant Path Model dialog.

Path Loss Exponents

The path loss exponents influence the propagation result computed by the DPM significantly. The path loss exponents describe the attenuation with distance. A higher path loss exponent leads to a higher attenuation in same distance. The following figure shows a comparison of three predictions with different path loss values for the LOS area.

Figure 3. Comparison of path loss predictions with different path loss values. LOS exponent 2.0 (on the left), LOS exponent 2.3 (middle) and LOS exponent 2.6 (to the right).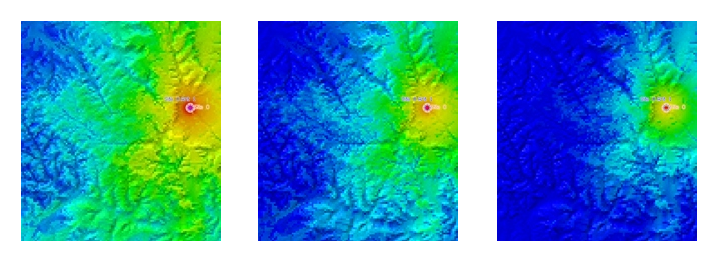

The following table shows recommended path loss exponents, depending on the height of the transmitter. The density of obstacles in the real scenario which are not modeled in the vector database do also influence the path loss exponent. The more objects that are missing in the vector database, the higher the path loss exponent should be.

Table 1. Recommended path loss exponents according to height of the transmitter.
Environment	High Transmitter	Low Transmitter
LOS before breakpoint	2.0	2.2
LOS after breakpoint	3.0	3.8
OLOS before breakpoint	2.2	2.3
OLOS after breakpoint	3.2	4.0

Note:

A high transmitter is mounted above obstacles in the vicinity (typically several meters or tens of meters).
A low transmitter is mounted between obstacles in the vicinity.

Losses

Each change in the direction of propagation due to an interaction (diffraction, transmission/penetration) along a propagation path causes an additional attenuation. The maximum attenuation can be defined. The effective interaction loss depends on the angle of the diffraction. It is recommended to select Auto. The transmitter frequency will then be taken into account in the calculation of maximum interaction loss.

Adaptive Resolution Management

For acceleration purposes, the DPM offers an adaptive resolution. In close streets a fine resolution is used for the prediction and on large places or open areas DPM switches automatically to a coarse resolution. The prediction time and the memory demand are positively influenced by the adaptive resolution but the accuracy is limited - especially if the highest level for the adaptive resolution is selected by the user.

Additional Features

The DPM supports additional features:

Consideration of clutter in rural/suburban environment: Clutter databases describe the land usage of scenarios and can be considered by the DPM.
Auto calibration of model parameters.

Auto Calibration

The model can be calibrated automatically.